Пример на действия с процентами. Все о процентах

Понятие процента имеет широкое практическое применение, поэтому оно является обязательной частью школьной программы по математике. Школьники должны научится решать основные задачи на проценты, представлять их в виде десятичных и обыкновенных дробей.

Традиционно тема «Проценты» изучается в рамках младших классов среднего звена. Можно выделить несколько подходов к изучению данной темы.

Первый подход. Рассмотрение процентов ведется как отдельная тема, без опоры на дроби. Нахождение нескольких процентов от числа осуществляется в два действия. Изучение дробей ведется отдельной темой, гораздо позже задач на проценты. Таким образом, обучение идет от частного к общему, что менее эффективно и дает меньше возможностей для развития обучаемого.

Второй подход. Задачи на проценты осваиваются как частный случай задач на дроби и все приемы решения переносятся на них, то есть изучение идет от общего случая - задач на дроби, к частному. В большинстве современных учебников реализован второй подход.

Рассмотрим более подробно изучение данной темы в некоторых современных учебниках, рекомендованных Министерством Образования России на 2003/2004 учебный год для преподавания математики в основной школе.

По учебникам , тема «Проценты» изучается в V классе. Перед введением понятия «процент» автор предлагает рассмотреть примеры:

«Сотую часть центнера называют килограммом, сотую часть метра - сантиметром, сотую часть гектара - акром. Принято называть сотую часть любой величины процентом».

Рассматриваются три основные задачи на проценты:

Задача вида К1 .

Пример 1: Бригада рабочих за день отремонтировала 40% дороги, имеющей длину 120 м. Сколько метров дороги было отремонтировано бригадой за день?

120 м составляет 100%

1) 120:100 =1,2 м составляет 1%.

2) м отремонтировано бригадой за день.

Ответ: За день бригада отремонтировала 48 м дороги.

Задача вида К2.

Пример 2: Ученик прочитал 72 страницы, что составляет 30% числа всех страниц книги. Сколько страниц в книге?

Неизвестное число - 100%.

1) 72:30=2,4 страницы составляет 1%.

2) страниц составляет 100%.

Ответ: В книге 240 страниц.

Задача вида П1 .

Пример 3: В классе из 40 учащихся 32 правильно решили задачу. Сколько процентов учащихся правильно решили задачу?

40 учащихся составляют 100%.

1) 40:100=0,4 составляет 1%.

2) 32:0,4=80; 32 ученика составляют 80%.

Ответ: 80% учащихся правильно решили задачу.

Однако эти виды задач не выделяются, так как в качестве основного способа решения задач на проценты принят способ приведения к единице. Он обладает определенными преимуществами:

а) проще для выполнения вычислений;

б) приучает учащихся к выделению числа, принимаемого за 100%;

в) требует проведения в процессе решения конкретной задачи соответствующих рассуждений, которые не включают запоминания правил решения того или иного вида задач на проценты.

Учебник предполагает решать некоторые задачи на проценты с помощью уравнений. Эта рекомендация относится по существу к двум видам задач: нахождение числа по данному числу его процентов и нахождение процентного отношения двух чисел. Опыт преподавания математики в V классе показывает, что учащиеся сталкиваются с определенными трудностями в процессе решения задач на проценты, что связано в основном с недостаточной осознанностью учащимися способа приведения к единице. Поэтому отработка сущности этого способа в два действия имеет решающее значение в обучении решению задач на проценты, особенно на начальном этапе усвоения знаний. Задачи, рассмотренные в примерах 2 и 3, могут быть решены с помощью уравнений. В V классе решение задач с помощью уравнений вызывают у учащихся значительные трудности.

Эта тема является одной из последних в курсе V класса. Далее авторы специально к теме не возвращается. Это не очень удачно, так как тема объективно трудная.

Несколько другой подход к этой теме в учебниках . Изучение процентов начинается в конце V класса. Авторы определяют процент, как иное название одной сотой. «Мы знаем, что одна вторая иначе называется половиной, одна четвертая - четвертью, три четвертых - тремя четвертями. Особое название имеет и одна сотая: одна сотая называется процентом». Учащиеся рассматривают только два вида задач:

Задача вида К1 .

Пример 4. В школе 800 учащихся, 15% из них за четверть получили пятерки по математике. Сколько учеников получили пятерки по математике?

Найдем вначале один процент, или одну сотую, от числа уча щихся.

800: 100=8.

Чтобы найти 15%, нужно выполнить умножение:

Ответ: 120 учеников получили пятерки.

Большое внимание уделяется связи дробей (десятичных и обыкновенных) и процентов.

Задача вида П1 .

Пример 5. Сколько процентов от 1 м составляет 1см, 9 см, 0,15 м?

В VI классе авторы снова возвращаются к этой теме. Учащиеся повторяют материал, изученный в V классе, и рассматриваются новые задачи. При этом для каждого вида задач проводится аналогия с действиями над десятичными и обыкновенными дробями, формулируется правило:

Для задачи вида К1.

2) умножить данное число на эту дробь»

А также для задачи вида К2.

«1) выразить проценты обыкновенной или десятичной дробью;

2) разделить данное число на эту дробь»

Пример 6. За контрольную работу по математике отметку «4» получили 9 учеников. Это составляет 36% от всех учащихся класса. Сколько учащихся в классе?

Выразим проценты обыкновенной или десятичной дробью: 36%= =0,36.

Воспользуемся правилом нахождения числа по его дроби:

9:==25 или 9:0,36=25

Ответ: в классе было 25 учащихся.

Сначала учащиеся рассматривают выражение частного двух чисел в процентах: «чтобы выразить частное в процентах, нужно частное умножить на 100 и к полученному произведению приписать знак процента».

Только после этого они переходят к решению задачи П1 .

«Для этого нужно

1) первое число разделить на вторе;

2) полученное частное выразить в процентах»

Пример 7. В классе 25 учащихся, из них 20 пионеров. Сколько процентов составляют пионеры?

Для решения нужно частное выразить в процентах. =0,8=80%.

Ответ: пионеры составляют 80%.

В конце темы рассматривается задача вида П2 и П3 .

«… чтобы узнать, на сколько процентов увеличилась или уменьшилась данная величина, необходимо найти:

1) на сколько единиц увеличилась или уменьшилась эта величина;

2) сколько процентов составляет полученная разность от первоначального значения величины»

Пример 8. До снижения цен холодильник стоил 250р., после снижения - 230 р. На сколько процентов снизилась стоимость холодильника?

Узнаем, на сколько рублей изменилась цена холодильника: 250-230=20 р.

Найдем, сколько процентов составляет полученная разность от первоначальной стоимости холодильника: =0,08=8%

Ответ: стоимость холодильника понизилась на 8%.

Правила ограничивают учащихся, не дают им рассуждать над решением. Поэтому каждая задача на проценты становится алгоритмом и вызывает затруднения, если правило забыто. Решение задач в данном курсе арифметическое. Использование уравнений при решении начинается лишь в конце года только в сложных задачах. Следовательно, не каждый ученик сможет овладеть этим умением. Поэтому нужно включить задачи на проценты при изучении уравнений.

В учебниках , понятие процента также изучается в конце V класса. Перед введением определения рассматриваются примеры употребления понятия «процент»:

«Всхожесть семян составляет 98 процентов; в выборах президента России приняли участие 65 процентов избирателей… ». Процент определяется как обозначение сотой доли. В V классе авторы рассматривают только два вида задач: задачи вида К1 и К2 . Решение этих задач осуществляется арифметическим способом. Большое внимание уделяется вопросу, какую величину взять за 100%.

Далее тема «Проценты» изучается в VI классе. Здесь рассматриваются те же виды задач, но решение осуществляется уже алгебраическим способом (составление линейных уравнений). Авторы формулируют правила нахождения части от целого и целого по его части:

«1) чтобы найти часть от целого, надо целое (соответствующее ему число) умножить на дробь (соответствующее этой части);

2) чтобы найти целое по его части, надо часть (соответствующее этой части число) разделить на соответствующую ей дробь».

После этого тема не рассматривается.

Несколько другой подход в учебниках , . Проценты начинают изучаться в начале VI класса. Вводится понятие процента как одной сотой части числа (величины). Рассматриваются задачи трех типов:

а) нахождение процентов от данного числа К1 .

Сначала рассматривается нахождение 1% от данного числа. Затем - нахождение произвольного числа процентов.

б) нахождение числа по данному числу его процентов К2 .

Также в первую очередь обсуждается, как найти число, 1% которого известен. Затем эта задача рассматривается для любого произвольного числа процентов.

в) нахождение процентного отношения двух чисел П1 . Авторы формулируют правило «Чтобы отношение двух чисел выразить в процентах, можно это отношение умножить на 100»

Все три типа задач решаются сначала арифметическим способом, а затем их решают, на основе свойств пропорциональности.

Пример 9. Найти 8% от 35.

Решение: Пусть x - искомое число, тогда:

Ответ: 2

Рассматриваются также задачи, в которых нужно увеличить (уменьшить) число на некоторое число процентов К3 и К4. Проценты также используются при изучении диаграмм.

Пример 10.

Цену товара увеличили на 10%, затем еще на 10%. На сколько процентов увеличили цену товара за два раза?

Здесь же рассматриваются задачи на смеси и сплавы (этот параграф отмечен, как параграф повышенной трудности). Мне кажется, что задачи такого типа для шестиклассников сложны. Поэтому не каждый учитель захочет рассматривать такие сложные задачи со всем классом и очень важный пласт задач останется не рассмотренным. Но это очень важные задачи, которым следует уделить должное внимание, возможно, в старшем возрасте.

В этом комплекте также уделяется внимание работе с калькулятором при решении задач на проценты. Данному вопросу посвящен отдельный параграф и разработана система упражнений.

В старших классах тема проценты рассматривается в рамках задач на повторение и задач повышенной трудности. В старших классах операции с процентами становятся прерогативой химии, которая внедряет свой взгляд на проценты. Поэтому вопросы универсальности процентов и разнообразия сфер их применения постепенно забываются учащимися.

Покажем, как предлагается изучать этот материал в учебных комплектах по математике для V-VI класса под ред. Г.В.Дорофеева и И.Ф. Шарыгина и для VII - IX класса под ред. Г.В.Дорофеева.

Прежде всего, нужно отметить, что при изложении темы «Проценты» реализуются многие общие методические особенности, характерные для курса в целом. Тема разворачивается по спирали и изучается в несколько этапов с VI по IX класс включительно. При каждом проходе учащиеся возвращаются к процентам на новом уровне, их знания пополняются, добавляются новые типы задач и приемы решений. Такое многократное обращение к понятию приводит к тому, что постепенно оно усваивается прочно и осознанно. Появляется возможность включать задачи, которые сейчас в действующих учебниках не могут рассматриваться просто в силу возрастных особенностей школьников.

Вопросы, связанные с процентами, позволяют сделать курс ориентированным на практику, показать учащимся, что приобретаемые ими математические знания применяются в повседневной жизни. Интерес в значительной степени поддерживается также и содержанием задач, фабулы которых приближены к современной тематике и к жизненному опыту детей, а затем и подростков. Это служит достаточно сильным мотивом для решения предлагаемых задач.

Введение процентов опирается на предметно-практическую деятельность школьников, на геометрическую наглядность и геометрическое моделирование. Широко используются рисунки и чертежи, помогающие разобраться в задаче и увидеть путь решения.

Как и во всех основных разделах курса при изложении этой темы реализованы широкие возможности для дифференцированного обучения учащихся. Задачи предлагаются в широком диапазоне сложности - от базовых, до достаточно трудных. Учитель может подобрать материал, соответствующий возможностям каждого школьника.

При обучении решению задач на проценты учащиеся знакомятся с разными способами решения задач, причем множество приемов шире, чем это бывает обычно. Ученик овладевает разнообразными способами рассуждения, обогащая свой арсенал приемов и методов. Но при этом также важно, что он имеет возможность выбора и может пользоваться тем приемом, который ему кажется более удобным.

, цикл статей про личные финансы.

Сегодня поговорим про проценты.

Невозможно инвестировать не понимая, что такое процент и как считается доходность.

С простыми процентами как правило проблем не бывает, каждый кто хоть раз держал деньги на депозите в банке понимает, что, например, ставка процента 10% годовых на вклад 50 000 руб. даст 5000 дохода за год.

Сложнее понять действие сложного процента, а он очень важен именно в долгосрочном инвестировании, т.е. когда инвестиции делаются с целью обеспечения финансовой свободы.

По сути при сложном проценте процентный доход вновь инвестируется, увеличивая размер вклада. Вот пример, допустим у вас есть 100 000 руб. и на них Вы получаете 10% дохода, т.е. 10 000 руб. в год.

В первый год Вы получили 10000 руб. и Ваш вклад увеличился на эти 10 000 составив 110 000 руб.

Во второй год Ваш доход уже составит 10% от 110 000 руб., т.е. 11000 руб., которые Вы также добавляете к вкладу, который становится уже 110 000 + 11 000 = 121 000 руб.

Третий год: Ваша 121 тысяча рублей приносит опять 10%, что в рублях 12100 руб., а Ваш вклад в конце третьего года составит 121 000 + 12100=133 100 руб.

И т.д.

В формализованном виде сложные проценты записываются так:

FV = PV (1 + r) ^ n

где FV – будущая стоимость вклада; PV – начальная стоимость вклада; r – ставка дохода (доходность); n – число периодов.

Ну проверьте формулу на нашем примере FV = 10000 (1 + 0,1)^3 = 133 100 руб. Как видите все сошлось 🙂

Когда Вы инвестируете на долгие сроки, тогда значение сложных процентов возрастает очень сильно.

Представьте себе такой пример, если молоко будет дорожать на 10% в год, сколько оно будет стоить через 20 лет? Если сегодня молоко стоит 30 рублей за литр, то допуская рост стоимости молока на 10% в год, через 20 лет молоко будет стоить FV = 30 (1+0,1)^20 = 201 рубль 82 копейки!

Этот пример кстати говоря очень хорошо показывает необходимость инвестирования, сохранения своих капиталов, так как они обесцениваются так же по формуле сложных процентов.

Эту формулу еще называют “формула Ротшильда”, “формула дьявола”, а на английском и в финансовых кругах это называется “компаундинг”.

Все на земле меняется по формуле сложных процентов: инфляция, рост потребления нефти или пшеницы, меняется население земли и т.д.

Когда Вы инвестируете процент работает за Вас, вот пример я раньше приводил по поводу пенсий :

Какую же сумму удастся накопить среднестатистическому россиянину, если он будет инвестировать по 3000 руб. в месяц в течение 30 лет? Предположим, что рост его инвестиций составит 5% в год, а доходность инвестиций будет равна 17% годовых.

Через 30 лет накопится 32 022 812 руб. Так сложный процент работает на Вас, выступая таким рычагом, увеличивающим ваш вклад.

Но он работает и против, когда Вы берете кредиты, например.

В принципе существуют программы, которые позволяют считать сложные проценты и связанные с ними формулы аннуитетов (аннуитетом считается ряд платежей, которые одинаковы (или меняются по закономерности) и отстоят друг от друга на одинаковый период времени, аннуитетом считается и пример с накоплением 3000 руб. в месяц выше и ежемесячная равная выплата по кредиту в течении времени).

Вы сами можете попробовать, я пользуюсь вот такой программой для iPad , она бесплатная, там у них есть варианты и для Android.

На рисунке показан пример расчета размера выплат по кредиту с использованием данной программы.

Там же можно будет попробовать и другие финансовые расчеты провести, например, подсчитать сложные проценты и аннуитеты.

Пробуйте, главное понять сам принцип.

Деньги настолько прочно вошли в нашу жизнь, что все мы — вне зависимости от возраста, пола и способа получения дохода время от времени попадаем в ситуации, когда мы вынуждены принимать решения, требующие финансовых расчетов. И тогда от нашей способности оперировать конкретными финансовыми категориями зависит, насколько выгодным будет выбранный нами вариант. В данной статье мы рассмотрим основные категории финансовой математики и покажем, как с их помощью принимать верные решения в самых различных ситуациях.

Проценты. Сложные проценты. Капитализация процентов (Compaunding)

Процентами называют доход, полученный в качестве платы за предоставление денег в долг в любой форме. Проценты могут выражаться в абсолютной и относительной форме. Абсолютная форма — это конкретная сумма за определенный период. Относительная — в виде процентной ставки, привязанной к оговоренному периоду (год, месяц или день). Чтобы рассчитать наращенную сумму (S), под которой мы будем понимать основную сумму плюс накопленные проценты, необходимо воспользоваться следующей формулой:

(1) S = P * (1 + i * n),
где P — сумма, на которую начисляется процент, i — процентная ставка, N — количество периодов начисления.

Пример
Вы предоставили знакомому заем в размере 10,000$ на 3 месяца, по условиям которого он обещает выплачивать вам 2% в месяц. Необходимо рассчитать сумму, которую вы получите в конце срока пользования займом. Получаем 10,000 * (1 + 2% * 3) = 10,600$.

Часто можно встретить ситуацию, когда проценты не выплачиваются, а присоединяются к вложенной сумме и с нового периода начисление производится уже на сумму с учетом присоединенных ранее процентов. Такой процент называется сложным, а процесс начисления процентов на процент — капитализацией процентов. В случае сложного процента наращенная сумма рассчитывается по-другому:

(2) S = P * (1 + i) ^ n,
где значение букв то же, что и в формуле выше, а знак «^» означает возведение в степень.

В чем отличие сложных и простых процентов? Если рост простых процентов происходит линейно (на одинаковую сумму каждый период), то сложные проценты растут экспоненциально (каждый последующий период сумма процентов больше, чем в предыдущий). Благодаря данному эффекту сумма, размещенная под сложный процент на длительный срок, многократно превосходит рост суммы, размещенной под простой процент. Ниже приведены результаты роста депозита (6% годовых) при простом и сложном проценте. Если в первое время разница остается небольшой, то в последствии одна достигает критического значения. Так, на 80 год на депозит с простым процентом достигнет 58,000$, в то время как депозит со сложным — 1,057,960$.

В практике часто встречается практика, при которой период начисления процентов отличается от целого числа. В такой ситуации, формула расчета наращенной суммы при простом проценте приобретает вид:

(3) S = P * (1 + i * d / 365),
где d — период начисления процентов, выраженный в днях.

Также встречаются ситуации, когда процентная ставка выражается в годовых, но начисление процента происходит ежемесячно. В таких случаях формула расчета наращенной суммы (как правило, в данном случае используются сложные проценты) будет иметь вид:

(4) S = P * (1 + i/m) ^ (n*m),
где m — количество периодов начисления процентов в рамках периода (обычно используется 12 по числу месяцев в году).

И напоследок обратим внимание, что вне зависимости от вида процента, все формулы по расчету наращенной суммы можно привести к общему виду:

(5) S = P * k,
где k — коэффициент наращения, который рассчитывается различными способами в зависимости от применяемого вида процента. Этот вывод существенно облегчит нам понимание последующих математических операций.

Дисконтирование и его сущность

Концепция процентов, которую мы рассмотрели выше, отражает временную стоимость денег. Иными словами, в силу того, что деньги, которыми мы владеем сегодня, завтра могут принести нам доход в результате их размещения под определенный процент, будущие денежные поступления имеют меньшую текущую стоимость. На этом принципе основывается математическая операция, которая получила название дисконтирование. Дисконтирование означает приведение будущих платежей к текущей стоимости и по смыслу является операцией, обратной наращению процентов. То есть дисконтирование рассматривает будущие платежи как наращенную сумму (S) и задача инвестора рассчитать их текущую стоимость (P) из расчета доступной ему процентной ставки (i). В зависимости от вида процента, формула дисконтирования будет иметь следующий вид: или

(6) P = S / (1 + i * n)

(7) P = S / (1 + i) ^ n

Задача дисконтирования показать нам, сколько деньги, которые мы получим в будущем, стоят сегодня, чтобы не переплатить за будущие платежи с точки зрения доступной нам инвестиционной альтернативы. Рассмотрим несколько распространенных операций, в которых применяется дисконтирование.

Приобретение потока будущих платежей (учетные операции)
К приобретению предлагается облигация номинальной стоимостью 1000$ с процентной ставкой 6% годовых, выплата процентов по которой производится ежеквартально, а погашение — в конце года. Задача — рассчитать текущую стоимость обязательства из расчета учетной ставки 15 % годовых.

Решение
Рассчитаем ежеквартальный процентный доход и построим в программе Excel таблицу денежных потоков. Найдем значение текущей стоимости с помощью встроенной формулы ЧПС. Таким образом, при учетной ставке в 15% годовых, текущая стоимость данного финансового обязательства равно 916,22$

Примечание

2) В формуле ЧПС на место процентной ставки ставим годовой процент, деленный на 12

Финансовая эквивалентность
Стороны согласовывают условия по оплате офисного помещения. Цена помещения — 24,000$. Продавец согласен на рассрочку платежа на следующих условиях: 8,000 $ сразу, остальное равными частями в течение 4 месяцев. Однако он готов рассмотреть и больший срок рассрочки, если продавец предложит ему большую сумму за продаваемое помещение.

Решение
Отразим первоначальные условия рассрочки в виде таблицы в программе Excel. Смоделируем в этой же таблице предложение с нарастающими ежемесячными платежами, по итогу которых цена помещения возрастет до 24,400$. Рассчитаем текущую стоимость каждого варианта для сопоставления их эквивалентности из расчета процентной ставки, равной 10% годовых. Из расчета видно, что второй вариант даже при условии более высокой цены покупки более выгоден для покупателя, чем первый

Консолидация платежей
Консолидацией платежей называют операцию по объединению нескольких платежных обязательств в один платеж (S0) в определенный срок (Т0). Особенность данной операции заключается в том, что все платежи, поступление которых ожидается раньше данного срока, рассчитываются наращением, а те, которые ожидаются после него — дисконтированием. В зависимости от вида используемого процента формула консолидации имеет следующий вид:

(8) S = ∑ Pn * (1 + i * (Т0 — Тn))

(9) S = ∑ Pn* (1 + i) ^ (Т0 — Тa))

Пример
Вы открыли банковский вклад 10,000$ на 12 месяцев под 10% годовых. Сколько денег вам необходимо положить на счет на 14 месяц, чтобы через 3 года у вас было на счету 15,000$.

Решение
Представим задачу в виде консолидации платежей, где существующий вклад будет выражен в виде положительного числа, а ожидаемая в будущем сумма — отрицательного. Учитывая, что процент начисляется по ставке сложного процента, получим следующий расчет 10,000 * (1 + 10% / 12) ^ (14-0) — 15,000 * (1 + 10% / 12) ^ (14-36) = 11,232 — 12,496 = -1,264$.

Определение внутренней ставки доходности

В бизнесе и инвестировании часто встречаются ситуации, когда инвестору известны будущие платежи и сумма вложений, и ему необходимо рассчитать коэффициент наращения, при котором сумма будущих платежей, приведенных к текущей стоимости, будет численно равна сумме вложений. Коэффициент наращения, для которого выполняется данное условие, называется внутренней ставкой доходности (ВСД, в англ. — IRR, internal return of return). Для расчета внутренней ставки доходности применяется встроенная функция программы Excel — ВСД.

Пример
Инвестор рассматривает инвестиционное предложение, которое представляет собой долевое участие в открытие пиццерии (см. здесь). Нам известны: а) сумма запрашиваемых инвестиций; б) финансовый план (прогноз денежных потоков); в) схема по распределению денежных потоков. Резюме инвестиционного предложения (см. таблицу) содержит 6 вариантов доходности. Необходимо определить общую доходность инвестиционного предложения для сравнения с иными вариантами инвестиций.

Решение
Построим в программе Excel таблицу денежных потоков, которые получит инвестор согласно финансового плана (см. таблицу). Рассчитаем внутреннюю ставку доходности с помощью встроенной формулы ВСД, где в качестве диапазона значений указываем все значения платежей, включая первоначальные инвестиции. Полученное значение внутренней ставки доходности (ВСД) = 38,47%. Таким образом, общая ожидаемая доходность рассматриваемого инвестиционного предложения составляет 38,47% годовых.

Примечание
1) В периоды, когда платежи отсутствует, ставим «0″.
2) Для получения годовой ставки ВСД полученное значение умножаем на 12.

Аннуитет (финансовая рента)
Поток платежей, все составляющие которого положительные величины, а временные интервалы между платежами одинаковы, называют аннуитетом или финансовой рентой. Например, аннуитетом является последовательность получения процентов по облигации, платежи по потребительскому кредиту, регулярные взносы по договорам накопительного страхования, выплата пенсий. Аннуитеты характеризуются следующими параметрами: 1) величиной каждого отдельного платежа; 2) интервалом между платежами; 3) продолжительностью платежей (бывают вечные анну­итеты); 4) процентной ставкой. В силу сложности расчетной формулы, для расчета различных составляющих аннуитета лучше всего использовать встроенные формулы программы Excel. Рассмотрим основные из них.

При расчете кредита используются формулы ПЛТ (рассчитывает сумму ежемесячного платежа), ОСПЛТ (рассчитывает сумму погашения основного долга в составе конкретного ежемесячного платежа), ПРПЛТ (рассчитывает сумму процентов в составе конкретного ежемесячного платежа).

Пример
Необходимо рассчитать ежемесячный платеж и составить график платежей по кредиту, сумма 10,000$, процентная ставка 20%, срок — 20 месяцев.

Решение
Для расчета платежа используем формулу ПЛТ. На место процентной ставки подставляем ежемесячное значение (годовое значение, деленное на 12), в качестве приведенной стоимости указываем сумму кредита, будущая стоимость — указываем 0. Те же значения используем для формул ОСПЛТ и ПРПЛТ, в которых меняется только порядковый номер периода. Полученные значения представим в виде таблицы:

Та же формула ПЛТ может использоваться для расчета ежемесячных взносов для накопления суммы к заданному моменту времени. Для этого на место приведенной стоимости ставим сумму первоначального взноса, а на место будущей стоимости — необходимую сумму.

Пример
Вам 25 лет. Вы открыли пенсионный накопительный счет с процентной ставкой в размере 6% годовых и положили на него ваши накопления в размере 10,000$. Рассчитаем размер ежемесячного платежа, который вам необходимо откладывать на счет, чтобы к 45 годам получить сумму в размере 100,000$.

Решение
Используем функцию ПЛТ. В качестве процентной ставки указываем 6% / 12, количество периодов — 20 * 12, приведенная стоимость — 10,000$, будущая стоимость — 100,000$. В данном случае заполненная формула будет выглядеть так =ПЛТ(6%/12;20*12;10000;100,000). Получаем сумму ежемесячного взноса в размере 288$.

Как вы заметили, в вышеуказанных примерах мы рассчитывали сумму ежемесячного платежа, иные параметры аннуитета нам были известны. Excel позволяет нам рассчитать и иные параметры аннуитета — приведенную стоимость, будущую стоимость, количество периодических платежей. Разберем на примерах как работают эти формулы.

Пример расчета приведенной стоимости
К 10-летию сына вы решили открыть накопительный счет, чтобы его 18-летию накопить на нем 10,000$. Какой первоначальный взнос вам необходимо внести на данный счет, если планируемые ежемесячные взносы составляют 50$?

Решение
Используем функцию ПС. В качестве процентной ставки указываем 6% / 12, количество платежей 8 * 12, периодический платеж — 50$, будущая стоимость — минус 10,000$. В данном случае заполненная формула будет выглядеть так =ПС(6%/12;8*12;50;-10000). Полученное значение первоначального взноса — 2390$.

Примечание
Отрицательное значение в формулах ПС и БС означает «я получу», положительное — «я плачу».

Пример расчета будущей стоимости и количества платежей
Два друга решили обеспечить себе дополнительную пенсию. Для этого каждый из них открыл накопительный счет с доходностью 6% годовых, один внес на него первоначальный взнос в размере 3,000$ , а второй — 5,000$. Первому 25 лет, второму 30, оба хотят выйти на пенсию к 45 годам. Оба готовы отчислять по 50$ ежемесячно. Необходимо рассчитать сумму их пенсионных накоплений и количество месяцев начисления пенсии за счет накопленных средств, если пенсионные выплаты планируются в размере 150$.

Решение
Вначале рассчитаем сумму пенсионных накоплений. Для этого используем формулу БС. В первом случае количество платежей будет равно 20 * 12, во втором — 15 * 12, приведенная стоимость в первом случае 3000$, во втором — 5000$, процентная ставка в обоих случаях будет равна 6% / 12, а периодический платеж — 50$. Собранная формула в первом случае будет выглядеть = БС(6%/12;20*12;50;3000), во втором = БС(6%/12;15*12;50;5000). В первом случае пенсионные накопления составят 33,032$, во втором — 26,811$. Теперь рассчитаем срок, в течение которой накопленная сумма может обеспечить указанные выше пенсионные выплаты. Для этого воспользуемся функцией КПЕР, где в качестве процентной ставки указываем 6%/12, в качестве суммы платежа ставим 150$, в качестве приведенной стоимости подставляем полученные значения. Получаем сумму в месяцах — 149 для первого и 128 для второго.

Примечание
Отрицательное значение в формуле показывает, что мы получаем платежи, в случае, если формула применяется для расчета платежей, которые необходимо оплатить, полученное значение будет положительным.

Вечная рента (перпетуитет) и модель Гордона

Частным случаем аннуитета является последовательность платежей, продолжительность которого условно не определена, в связи с чем данный аннуитет считается вечным. Примером вечного аннутитета могут быть консоли — разновидность ценных бумаг (облигаций), по которым проценты начисляются бессрочно, но возврат номинальной стоимости не производится. На практике, такие ценные бумаги встречаются достаточно редко. Более распространенным примером вечного аннуитета являются дивидендные платежи, которые длительное время выплачиваются некоторыми компаниями своим акционерам. Для расчета стоимости вечного аннуитета используется модель Гордона:

(10) S = P * (1+g) / (r — g) , где S — стоимость аннуитета, P — текущий платеж, g — темп роста текущего платежа, r — норма доходности.

Вышеуказанные формулы является основным перечнем инструментов для вычислений различного рода и позволяют произвести расчеты в отношении любой ситуации. В комментариях к данной статье вы можете описывать ситуации, требующие финансовых расчетов, а я постараюсь показать, как вышеуказанный математический аппарат поможет вам в их решении.

При подготовке статьи использовались материалы из учебного пособия «Финансовая математика» Ширшова Е.В., Н.И. Петрика, Тутыгина А.Г., Меньшикова Т.В., Москва, изд. «Кнорус», 2010 г.

Рассмотрим пример:

Цена холодильника в магазине за год увеличилась на. Какой стала цена, если изначально холодильник стоил руб?

Решение:

Для начала определим, на сколько рублей изменилась (в данном случае - увеличилась) стоимость холодильника.

По условию - на.

Но от чего?

Конечно же, от самой начальной стоимости холодильника - руб.

Получается, что нам нужно найти от руб:

Теперь мы знаем, что цена увеличилась на руб.

Остается только, согласно правилу, прибавить к начальной стоимости величину изменения:

Новая цена рублей.

Еще пример (постарайся решить самостоятельно):

Книга «Математика для чайников» в магазине стоит руб. Во время акции все книги продаются со скидкой

Сколько теперь придется заплатить за эту книгу?

Решение:

Что такое скидка, ты наверняка знаешь? Скидка в означает, что стоимость товара уменьшили на

На сколько уменьшилась стоимость книги (в рублях)?

Нужно найти от начальной ее стоимости в руб:

Цена уменьшилась, значит нужно из начальной стоимости вычесть то, на сколько она уменьшилась:

Новая цена рублей.

Правда ведь просто?

Но есть способ сделать это решение еще проще и короче!

Рассмотрим пример:

Увеличьте число на.

Чему равны от?

Как мы уже выяснили раньше, это будет.

Теперь увеличим само число x на эту величину:

Получается, что в результате мы к десятичной записи прибавили и умножили на число.

Обобщим это правило:

Пусть нам нужно увеличить число на.

от числа - это.

Тогда новое число будет равно: .

Например, увеличим число на:

А теперь попробуй сам:

1. Увеличить число на
2. Увеличить число на
3. На сколько процентов число больше числа?

Решения:

3) Пусть искомое количество процентов равно.

Это значит, что если число увеличить на, получится:

Ответ: на.

Если число x надо уменьшить на, все аналогично:

Итак, правило:

Примеры:

1) Уменьшить число на.

2) На сколько процентов число меньше числа?

3) Цена товара со скидкой в равна р. Чему равна цена без скидки?

Решения:

2) Число уменьшили на x процентов и получили:

Ответ: на.

3) Пусть цена без скидки равна. Получается, что x уменьшили на и получили:

Напоследок рассмотрим еще один тип задач, частенько вызывающих недоумение.

Решение сложных задач на проценты

Число больше числа на. На сколько процентов число меньше числа?

Что за странный вопрос: конечно же на!

Правильно?

А вот и нет.

Если, например, масса одного шкафа на 25 кг больше массы другого, то, без сомнения, масса второго шкафа на 25 кг меньше массы первого.

Но с процентами так не прокатит!

Ведь в первом случае, когда говорим, что число на больше числа, мы считаем от числа; а во втором случае, когда говорим, что число на меньше числа, мы считаем от числа. А поскольку числа и разные, то и от этих чисел будут разными!

Чтобы решить эту задачу верно, давай запишем условие в виде уравнения:

Число больше числа на. Это значит, что если число увеличить на, получим число:

Теперь в таком ж виде запишем вопрос: если число a уменьшить на процентов , получим число:

Выразим число из равенства (1):

И подставим в (2):

Отсюда следует, что:

Итак, получаем, что число на меньше числа!

Подобные задачи часто попадаются в ЕГЭ

Например:

В понедельник акции компании подорожали на некоторое число процентов , а во вторник подешевели на то же самое число процентов . В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

Решение:

Пусть цена акции в понедельник была равна, а искомое количество процентов , записанное в виде десятичной дроби (то есть, уже поделенное на), равно.

Запишем формулой, чему равна стоимость акции после подорожания:

При этом известно, что эта конечная цена на меньше начальной цены. То есть, если уменьшить на, получим:

Подставим, выраженное ранее:

Согласно здравому смыслу подходит только положительное решение:

Вспомним теперь, что это пока только десятичная запись искомого количества процентов , то есть это количество процентов , деленное на. Чтобы перевести в проценты , нужно домножить на 100%:

Где мы используем проценты в жизни?

Ну например в банковских продуктах: вкладах, кредитах, ипотеке и т.д

Если ты хорошо понимаешь, что такое проценты и умеешь решать уравнения, то ты без труда расчитаешь, например, размер ежемесячного платежа по кредиту.

Или сколько придется переплатить, взяв ипотеку. Такая задача есть в ЕГЭ под номером 17.

Проценты. Коротко о главном

Один процент любого числа - это одна сотая этого числа.

1. Проценты и десятичные дроби

2. Изменение числа на сколько-то процентов

Допустим, нужно увеличить число на.

от числа - это.

Тогда, новое число будет равно: .

Чтобы увеличить число на, нужно умножить его на.

Если число надо уменьшить на, то:

Уменьшить число на какую-то величину - значит вычесть из него эту величину:

Чтобы уменьшить число на, нужно умножить его на.

Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на проценты. Мы рассмотрим несколько задач, а также затронем те моменты, которые не упоминали ранее при изучении процентов, посчитав что на первых порах они создают трудности для обучения.

Большинство задач на проценты сводятся к тому, чтобы найти процент от числá, найти число по проценту, выразить в процентах какую-либо часть, либо выразить в процентном соотношении взаимосвязь между несколькими объектами, числами, величинами.

Предварительные навыки Содержание урока

Способы нахождения процента

Процент можно находить различными способами. Самый популярный способ — разделить число на 100 и умножить полученный результат на искомое количество процентов.

Например, чтобы найти 60% от 200 рублей, нужно сначала эти 200 рублей разделить на сто равных частей:

200 руб: 100 = 2 руб.

Когда мы делим число на 100, мы тем самым находим один процент от этого числа. Так, разделив 200 рублей на 100 частей, мы автоматически нашли 1% от двухсот рублей, то есть узнали сколько рублей прихóдится на одну часть. Как видно из примера, на одну часть (на один процент) приходится 2 рубля.

1% от 200 рублей — 2 рубля

Зная сколько рублей приходится на одну часть (на 1%), можно узнать сколько рублей приходится на две части, на три, на четыре, на пять и т.д. То есть можно найти любое количество процентов. Для этого достаточно умножить эти 2 рубля на искомое количество частей (процентов). Давайте найдём шестьдесят частей (60%)

2 руб × 60 = 120 руб.

2 руб × 5 = 10 руб.

Найдем 90%

2 руб × 90 = 180 руб.

Найдем 100%

2 руб × 100 = 200 руб.

100% это все сто частей и они составляют все 200 рублей.

Второй способ заключается в том, чтобы представить проценты в виде обыкновенной дроби и найти эту дробь от того числа, откуда требуется найти процент.

Например, найдем те же 60% от 200 рублей. Сначала предстáвим 60% в виде обыкновенной дроби. 60% это шестьдесят частей из ста, то есть шестьдесят сотых:

Теперь задание можно понимать как «найти от 200 рублей « . Это , которое мы изучали ранее. Напомним, что для нахождения дроби от числа, нужно это число разделить на знаменатель дроби и полученный результат умножить на числитель дроби

200: 100 = 2

2 × 60 = 120

Либо умножить число на дробь ():

Третий способ заключается в том, чтобы представить процент в виде десятичной дроби и умножить число на эту десятичную дробь.

Например, найдем те же 60% от 200 рублей. Для начала представляем 60% в виде дроби. 60% процентов это шестьдесят частей из ста

Выполним деление в этой дроби. Перенесем запятую в числе 60 на две цифры влево:

Теперь находим 0,60 от 200 рублей. Для нахождения десятичной дроби от числа, нужно это число умножить на десятичную дробь:

200 × 0,60 = 120 руб.

Приведенный способ нахождения процента является наиболее удобным, особенно если человек привык пользоваться калькулятором. Этот способ позволяет найти процент в одно действие.

Как правило выразить процент в десятичной дроби не составляет особого труда. Достаточно приписать «ноль целых» перед процентной долей, если процентная доля представляет собой двузначное число, или приписать «ноль целых» и еще один ноль, если процентная доля представляет собой однозначное число. Примеры:

60% = 0,60 — приписали ноль целых перед числом 60, поскольку число 60 является двузначным

6% = 0,06 — приписали ноль целых и еще один ноль перед числом 6, поскольку число 6 является однозначным.

При делении на 100 мы воспользовались методом передвижения запятой на две цифры влево. В ответе 0,60 ноль, стоящий после цифры 6, сохранился. Но если выполнить это деление уголком, ноль исчезает — получается ответ 0,6

Надо помнить, что десятичные дроби 0,60 и 0,6 равны одному и тому же значению:

0,60 = 0,6

В том же «уголке» можно продолжать деление бесконечно, каждый раз приписывая к остатку ноль, но это будет бессмысленным действием:

Выражать проценты в виде десятичной дроби можно не только делением на 100, но и умножением. Значок процента (%) сам по себе заменяет собой множитель 0,01. А если учитывать, что число процентов и значок процента записаны слитно, то между ними располагается «невидимый» знак умножения (×).

Так, запись 45% на самом деле выглядит следующим образом:

Заменим знак процента на множитель 0,01

Данное умножение на 0,01 выполнятся путем перемещения запятой на две цифры влево:

Задача 1 . Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 70% — деньги, заработанные папой. Какую часть заработала мама?

Решение

Всего процентов 100. Если папа заработал 70% денег, то остальные 30% денег заработала мама.

Задача 2 . Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 70% — деньги, заработанные папой, а 30% — деньги, заработанные мамой. Сколько денег заработал каждый?

Решение

Найдем 70 и 30 процентов от 75 тыс. рублей. Так мы определим сколько денег заработал каждый. Для удобства 70% и 30% запишем в виде десятичных дробей:

75 × 0,70 = 52,5 (тыс. руб. заработал папа)

75 × 0,30 = 22,5 (тыс. руб. заработала мама)

Проверка

52,5 + 22,5 = 75

75 = 75

Ответ : 52,5 тыс. руб. заработал папа, 22,5 руб. заработала мама.

Задача 3 . При остывании хлеб теряет до 4% своей массы в результате испарения воды. Сколько килограммов испарится при остывании 12 тонн хлеба.

Решение

Переведем 12 тонн в килограммы. В одной тонне тысяча килограмм, а в 12 тоннах в 12 раз больше:

1000 × 12 = 12 000 кг

Теперь найдем 4% от 12000. Полученный результат и будет ответом к задаче:

12 000 × 0,04 = 480 кг

Ответ : при остывании 12 тонн хлеба испарится 480 килограмм.

Задача 4 . Яблоки при сушке теряют 84% своей массы. Сколько получится сушенных яблок из 300 кг свежих?

Найдем 84% от 300 кг

300: 100 × 84 = 252 кг

300 кг свежих яблок в результате сушки потеряют 252 кг своей массы. Чтобы ответить на вопрос сколько получится сушенных яблок, нужно из 300 вычесть 252

300 − 252 = 48 кг

Ответ : из 300 кг свежих яблок получится 48 кг сушенных.

Задача 5 . В семенах сои содержится 20% масла. Сколько масла содержится в 700 кг сои?

Решение

Найдем 20% от 700 кг

700 × 0,20 = 140 кг

Ответ : в 700 кг сои содержится 140 кг масла

Задача 6 . Гречневая крупа содержит 10% белков, 2,5% жиров и 60% углеводов. Сколько этих продуктов содержится в 14,4 ц гречневой крупы?

Решение

Переведем 14,4 центнера в килограммы. В одном центнере 100 килограмм, в 14,4 центнерах в 14,4 раз больше

100 × 14,4 = 1440 кг

Найдем 10%, 2,5% и 60% от 1440 кг

1440 × 0,10 = 144 (кг белков)

1440 × 0,025 = 36 (кг жиров)

1440 × 0,60 = 864 (кг углеводов)

Ответ : в 14,4 ц гречневой крупы содержится 144 кг белков, 36 кг жиров, 864 кг углеводов.

Задача 7 . Для лесопитомника школьники собрали 60 кг семян дуба, акации, липы и клена. Желуди составляли 60%, семена клена 15%, семена липы 20% всех семян, а остальное составляли семена акации. Сколько килограммов семян акации было собрано школьниками?

Решение

Примем за 100% семена дуба, акации, липы и клена. Вычтем из этих 100% проценты, выражающие семена дуба, липы и клена. Так мы узнаем сколько процентов составляют семена акации:

100% − (60% + 15% + 20%) = 100% − 95% = 5%

Теперь находим семена акации:

60 × 0,05 = 3 кг

Ответ : школьниками было собрано 3 кг семян акации.

Проверка :

60 × 0,60 = 36

60 × 0,15 = 9

60 × 0,20 = 12

60 × 0,05 = 3

36 + 9 + 12 + 3 = 60

60 = 60

Задача 8 . Купил человек продукты. Молоко стоит 60 рублей, что составляет 48% от стоимости всех покупок. Определить общую сумму денег, потраченных на продукты.

Решение

Это задача на нахождение числа по его проценту, то есть по его известной части. Такую задачу можно решать двумя способами. Первый заключается в том, чтобы выразить известное число процентов в виде десятичной дроби и найти неизвестное число по этой дроби

Выразим 48% в виде десятичной дроби

48% : 100 = 0,48

Зная, что 0,48 составляет 60 рублей, мы можем определить сумму всех покупок. Для этого нужно найти неизвестное число по десятичной дроби:

60: 0,48 = 125 рублей

Значит, общая сумма денег, затраченных на продукты составляет 125 рублей.

Второй способ заключается в том, чтобы сначала узнать сколько денег приходится на один процент, затем полученный результат умножить на 100

48% это 60 рублей. Если мы разделим 60 рублей на 48, то узнаем сколько рублей приходится на 1%

60: 48% = 1,25 рублей

На 1% приходится 1,25 рублей. Всего процентов 100. Если мы умножим 1,25 рублей на 100, получим общую сумму денег, затраченных на продукты

1,25 × 100 = 125 рублей

Задача 9 . Из свежих слив выходит 35% сушенных. Сколько надо взять свежих слив, чтобы получить 140 кг сушенных? Сколько получится сушенных слив из 600 кг свежих?

Решение

Выразим 35% в виде десятичной дроби и найдем неизвестное число по этой дроби:

35% = 0,35

140: 0,35 = 400 кг

Чтобы получить 140 кг сушенных слив, нужно взять 400 кг свежих.

Ответим на второй вопрос задачи — сколько получится сушенных слив из 600 кг свежих? Если из свежих слив выходит 35% сушенных, то достаточно найти эти 35% от 600 кг свежих слив

600 × 0,35 = 210 кг

Ответ : чтобы получить 140 кг сушенных слив, нужно взять 400 кг свежих. Из 600 кг свежих слив получится 210 кг сушенных.

Задача 10 . Усвоение жиров организмом человека составляет 95%. За месяц ученик употребил 1,2 кг жиров. Сколько жиров может быть усвоено его организмом?

Решение

Переведем 1,2 кг в граммы

1,2 × 1000 = 1200 г

Найдем 95% от 1200 г

1200 × 0,95 = 1140 г

Ответ : 1140 г жиров может быть усвоено организмом ученика.

Выражение чисел в процентах

Процент, как было сказано ранее, можно представить в виде десятичной дроби. Для этого достаточно разделить число этих процентов на 100. Например, представим 12% в виде десятичной дроби:

Замечание. Мы сейчас не находим процент от чего-то, а просто записываем его в виде десятичной дроби .

Но возможен и обратный процесс. Десятичная дробь может быть представлена в виде процента. Для этого нужно умножить эту дробь на 100 и поставить знак процента (%)

Представим десятичную дробь 0,12 в виде процентов

0,12 × 100 = 12%

Это действие называют выражением числа в процентах или выражением чисел в сотых долях .

Умножение и деление являются обратными операциями. К примеру, если 2 × 5 = 10, то 10: 5 = 2

Точно так же деление можно записать в обратном порядке. Если 10: 5 = 2, то 2 × 5 = 10:

Тоже самое происходит, когда мы выражаем десятичную дробь в виде процентов. Так, 12% были выражены в виде десятичной дроби следующим образом: 12: 100 = 0,12 но потом эти же 12% были «возвращены» с помощью умножения, записав выражение 0,12 × 100 = 12%.

Аналогично можно выразить в процентах любые другие числа, в том числе и целые. Например, выразим в процентах число 3. Умножим данное число на 100 и к полученному результату добавим знак процента:

3 × 100 = 300%

Большие проценты вида 300% поначалу могут сбивать с толку, поскольку человек привык считать 100% максимальной долей. Из дополнительных сведений о дробях мы знаем, что один целый объект можно обозначать через единицу. К примеру, если имеется целый не разрезанный торт, то его можно обозначить через 1

Этот же торт можно обозначить как 100% торта. В этом случае и единица и 100% будут обозначать один и тот же целый торт:

Разрежем торт пополам. В этом случае единица обратится в десятичное число 0,5 (поскольку это половина единицы), а 100% обратятся в 50% (поскольку 50 это половина от сотни)

Вернем обратно целый торт, единицу и 100%

Изобразим ещё два таких торта с такими же обозначениями:

Если один торт является единицей, то три торта являются тремя единицами. Каждый торт является целым стопроцентным. Если сложить эти три сотни получится 300%.

Поэтому при переводе целых чисел в проценты, мы умножаем эти числа на 100.

Задача 2 . Выразить в процентах число 5

5 × 100 = 500%

Задача 3 . Выразить в процентах число 7

7 × 100 = 700%

Задача 4 . Выразить в процентах число 7,5

7,5 × 100 = 750%

Задача 5 . Выразить в процентах число 0,5

0,5 × 100 = 50%

Задача 6 . Выразить в процентах число 0,9

0,9 × 100 = 90%

Пример 7 . Выразить в процентах число 1,5

1,5 × 100 = 150%

Пример 8 . Выразить в процентах число 2,8

2,8 × 100 = 280%

Задача 9 . Джордж идет со школы домой. Первые пятнадцать минут он прошел 0,75 пути. В остальное время он прошел оставшиеся 0,25 пути. Выразите в процентах части пути, пройденные Джорджом.

Решение

0,75 × 100 = 75%

0,25 × 100 = 25%

Задача 10 . Джона угостили половиной яблока. Выразите эту половину в процентах.

Решение

Половина яблока записывается в виде дроби 0,5. Чтобы выразить эту дробь в процентах, умножим её на 100 и к полученному результату добавим знак процента

0,5 × 100 = 50%

Аналоги в виде дробей

Величина, выраженная в процентах, имеет свой аналог в виде обычной дроби. Так, аналогом для 50% является дробь . Пятьдесят процентов также можно назвать словом «половина».

Аналогом для 25% является дробь . Двадцать пять процентов также можно назвать словом «четверть».

Аналогом для 20% является дробь . Двадцать процентов также можно назвать словами «пятая часть».

Аналогом для 40% является дробь .

Аналогом для 60% является дробь

Пример 1 . Пять сантиметров это 50% от дециметра или или же просто половина. Во всех случаях речь идет об одной и той же величине — пяти сантиметрах из десяти

Пример 2 . Два с половиной сантиметра это 25% от дециметра или или же просто четверть

Пример 3 . Два сантиметра это 20% от дециметра или

Пример 4 . Четыре сантиметра это 40% от дециметра или

Пример 5 . Шесть сантиметров это 60% от дециметра или

Уменьшение и увеличение процентов

При увеличении или уменьшении величины, выраженной в процентах употребляется предлог «на».

Примеры :

• Увеличить на 50% — означает увеличить величину в 1,5 раза;
• Увеличить на 100% — означает увеличить величину в 2 раза;
• Увеличить на 200% — означает увеличить в 3 раза;
• Уменьшить на 50% — означает уменьшить величину в 2 раза;
• Уменьшить на 80% — означает уменьшить в 5 раз.

Пример 1 . Десять сантиметров увеличили на 50%. Сколько сантиметров получилось?

Чтобы решать подобные задачи, нужно исходную величину принимать за 100%. Исходная величина это 10 см. 50% от них составляют 5 см

Изначальные 10 см увеличили на 50% (на 5 см), значит получилось 10+5 см, то есть 15 см

Аналогом же увеличения десяти сантиметров на 50% является множитель 1,5. Если умножить на него 10 см получится 15 см

10 × 1,5 = 15 см

Поэтому выражения «увеличить на 50%» и «увеличить в 1,5 раза» говорят об одном и том же.

Пример 2 . Пять сантиметров увеличили на 100%. Сколько сантиметров получилось?

Примем исходные пять сантиметров за 100%. Сто процентов от этих пяти сантиметров будут сами 5 см. Если увеличить 5 см на эти же 5 см, то получится 10 см

Аналогом же увеличения пяти сантиметров на 100% является множитель 2. Если умножить на него 5 см получится 10 см

5 × 2 = 10 см

Поэтому выражения «увеличить на 100%» и «увеличить в 2 раза» говорят об одном и том же.

Пример 3 . Пять сантиметров увеличили на 200%. Сколько сантиметров получилось?

Примем исходные пять сантиметров за 100%. Двести процентов это два раза по сто процентов. То есть 200% от 5 см будут составлять 10 см (по 5 см на каждые 100%). Если увеличить 5 см на эти 10 см, то получится 15 см

Аналогом же увеличения пяти сантиметров на 200% является множитель 3. Если умножить на него 5 см получится 15 см

5 × 3 = 15 см

Поэтому выражения «увеличить на 200%» и «увеличить в 3 раза» говорят об одном и том же.

Пример 4 . Десять сантиметров уменьшили на 50%. Сколько сантиметров осталось?

Примем исходные 10 см за 100%. Пятьдесят процентов от 10 см составляют 5 см. Если уменьшить 10 см на эти 5 см, останется 5 см

Аналогом же уменьшения десяти сантиметров на 50% является делитель 2. Если разделить на него 10 см, то получится 5 см

10: 2 = 5 см

Поэтому выражения «уменьшить на 50%» и «уменьшить в 2 раза» говорят об одном и том же.

Пример 5 . Десять сантиметров уменьшили на 80%. Сколько сантиметров осталось?

Примем исходные 10 см за 100%. Восемьдесят процентов от 10 см составляют 8 см. Если уменьшить 10 см на эти 8 см, останется 2 см

Аналогом же уменьшения десяти сантиметров на 80% является делитель 5. Если разделить на него 10 см, то получится 2 см

10: 5 = 2 см

Поэтому выражения «уменьшить на 80%» и «уменьшить в 5 раз» говорят об одном и том же.

При решении задач на уменьшение и увеличение процентов, можно умножать/делить величину на указанный в задаче множитель.

Задача 1 . Насколько процентов изменилась величина, если она увеличилась в 1,5 раза?

Величину о которой говорится в задаче можно обозначить как 100%. Далее умножить эти 100% на множитель 1,5

100% × 1,5 = 150%

Теперь из полученных 150% вычтем изначальные 100% и получим ответ к задаче:

150% − 100% = 50%

Задача 2 . Насколько процентов изменилась величина, если она уменьшилась в 4 раза?

В этот раз будет происходить уменьшение величины, поэтому будем выполнять деление. Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 4

Из изначальных 100% вычтем полученные 25% и получим ответ к задаче:

100% − 25% = 75%

Значит, при уменьшении величины в 4 раза она уменьшилась на 75%.

Задача 3 . Насколько процентов изменилась величина, если она уменьшилась в 5 раз?

Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 5

Из изначальных 100% вычтем полученные 20% и получим ответ к задаче:

100% − 20% = 80%

Значит, при уменьшении величины в 5 раз она уменьшилась на 80%.

Задача 4 . Насколько процентов изменилась величина, если она уменьшилась в 10 раз?

Величину о которой говорится в задаче обозначим как 100%. Далее разделим эти 100% на делитель 10

Из изначальных 100% вычтем полученные 10% и получим ответ к задаче:

100% − 10% = 90%

Значит, при уменьшении величины в 10 раз она уменьшилась на 90%.

Задача на нахождение процентного соотношения

Чтобы выразить что-либо в процентном соотношении, сначала нужно записать дробь, показывающую какую часть первое число составляет от второго, затем выполнить деление в этой дроби и полученный результат выразить в процентах.

Например, пусть имеется пять яблок. При этом два яблока являются красными, три — зелеными. Выразим красные и зеленые яблоки в процентном соотношении.

Сначала нужно узнать какую часть составляют красные яблоки. Всего яблок пять, а красных два. Значит, два из пяти или две пятых составляют красные яблоки:

Зеленых же яблок три. Значит, три из пяти или три пятых составляют зеленые яблоки:

Имеем две дроби и . Выполним деление в этих дробях

Получили десятичные дроби 0,4 и 0,6. Теперь выразим в процентах эти десятичные дроби:

0,4 × 100 = 40%

0,6 × 100 = 60%

Значит, 40% составляют красные яблоки, 60% — зеленые.

А все пять яблок составляют 40%+60%, то есть 100%

Задача 2 . Двум сыновьям мама дала 200 рублей. Младшему брату мама дала 80 рублей, а старшему 120 рублей. Выразите в процентном соотношении деньги, данные каждому брату.

Решение

Младший брат получил 80 рублей из 200 рублей. Записываем дробь восемьдесят двухсотых:

Старший брат получил 120 рублей из 200 рублей. Записываем дробь сто двадцать двухсотых:

Имеем дроби и . Выполним деление в этих дробях

Выразим в процентах полученные результаты:

0,4 × 100 = 40%

0,6 × 100 = 60%

Значит, 40% денег получил младший брат, а 60% — старший.

Некоторые дроби, показывающие какую часть первое число составляет от второго, можно сокращать.

Так дроби и можно было бы сократить. От этого ответ к задаче не изменился бы:

Задача 3 . Бюджет семьи составляет 75 тыс. рублей в месяц. Из них 52,5 тыс. руб. — деньги, заработанные папой. 22,5 тыс. руб. — деньги, заработанные мамой. Выразите в процентах деньги, заработанные папой и мамой.

Решение

Данная задача, как и предыдущая, является задачей на нахождение процентного соотношения.

Выразим в процентах деньги, заработанные папой. Он заработал 52,5 тыс. рублей из 75 тыс. рублей

Выполним деление в этой дроби:

0,7 × 100 = 70%

Значит, папа заработал 70% денег. Далее нетрудно догадаться, что остальные 30% денег заработала мама. Ведь 75 тыс. рублей это все 100% денег. Для уверенности сделаем проверку. Мама заработала 22,5 тыс. руб. из 75 тыс. руб. Записываем дробь, выполняем деление и выражаем в процентах полученный результат:

Задача 4 . Школьник тренируется делать подтягивания на перекладине. В прошлом месяце он мог делать 8 подтягиваний за подход. В этом месяце он может делать 10 подтягиваний за подход. На сколько процентов он увеличил количество подтягиваний?

Решение

Узнаем на сколько больше подтягиваний школьник делает в текущем месяце, чем в прошлом

Узнаем какую часть два подтягивания составляют от восьми подтягиваний. Для этого найдем отношение 2 к 8

Выполним деление в этой дроби

Выразим полученный результат в процентах:

0,25 × 100 = 25%

Значит, школьник увеличил количество подтягиваний на 25%.

Эту задачу можно решить и вторым, более быстрым методом — узнать во сколько раз 10 подтягиваний больше, чем 8 подтягиваний и полученный результат выразить в процентах.

Чтобы узнать во сколько раз десять подтягиваний больше восьми подтягиваний, нужно найти отношение 10 к 8

Выполним деление в получившейся дроби

Выразим полученный результат в процентах:

1,25 × 100 = 125%

Показатель подтягиваний в текущем месяце составляет 125%. Данное высказывание нужно понимать именно как «составляет 125%» , а не как «показатель увеличился на 125%» . Это два разных высказывания, выражающих различные количества.

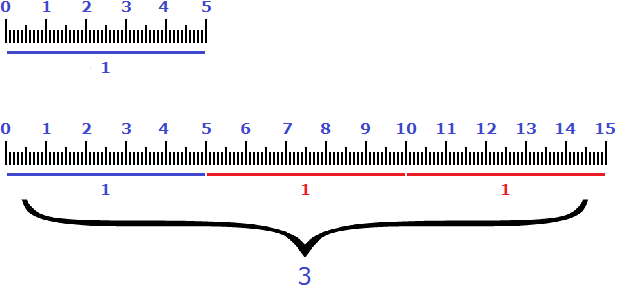
Высказывание «составляет 125%» нужно понимать как «восемь подтягиваний, которые составляют 100% плюс два подтягивания, которые составляют 25% от восьми подтягиваний». Графически это выглядит следующим образом:

А высказывание «увеличился на 125%» нужно понимать как «к текущим восьми подтягиваниях, которые составляли 100% добавились еще 100% (еще 8 подтягиваний) плюс еще 25% (2 подтягивания)». Итого получается 18 подтягиваний

100% + 100% + 25% = 8 + 8 + 2 = 18 подтягиваний

Графически это высказывание выглядит следующим образом:

Всего же получается 225%. Если найти 225% от восьми подтягиваний, мы получим 18 подтягиваний

8 × 2,25 = 18

Задача 5 . В прошлом месяце зарплата составляла 19,2 тыс. руб. В текущем месяце она составила 20,16 тыс. руб. На сколько процентов повысилась зарплата?

Эту задачу как и предыдущую можно решать двумя способами. Первый заключается в том, чтобы сначала узнать на сколько рублей увеличилась зарплата. Далее узнать какую часть эта прибавка составляет от зарплаты прошлого месяца

Узнаем на сколько рублей повысилась зарплата:

20,16 − 19,2 = 0,96 тыс. руб.

Узнаем какую часть 0,96 тыс. руб. составляет от 19,2. Для этого найдем отношение 0,96 к 19,2

Выполним деление в получившейся дроби. По пути вспомним, :

Выразим полученный результат в процентах:

0,05 × 100 = 5%

Значит, зарплата повысилась на 5%.

Решим задачу вторым способом. Узнаем во сколько раз 20,16 тыс. руб. больше, чем 19,2 тыс. руб. Для этого найдем отношение 20,16 к 19,2

Выполним деление в получившейся дроби:

Выразим полученный результат в процентах:

1,05 × 100 = 105%

Зарплата составляет 105%. То есть сюда входят 100%, которые составляли 19,2 тыс. руб., плюс 5% которые составляют 0,96 тыс. руб.

100% + 5% = 19,2 + 0,96

Задача 6 . Цена ноутбука в этом месяце повысилась на 5%. Какова его цена, если в прошлом месяце он стоил 18,3 тыс. рублей?

Решение

Найдем 5% от 18,3:

18,3 × 0,05 = 0,915

Прибавим эти 5% к 18,3:

18,3 + 0,915 = 19,215 тыс. руб.

Ответ : цена ноутбука составляет 19,215 тыс. руб.

Задача 7 . Цена ноутбука в этом месяце снизилась на 10%. Какова его цена, если в прошлом месяце он стоил 16,3 тыс. рублей?

Решение

Найдем 10% от 16,3:

16,3 × 0,10 = 1,63

Вычтем эти 10% из 16,3:

16,3 − 1,63 = 14, 67 (тыс. рублей)

Подобные задачи можно записывать кратко:

16,3 − (16,3 × 0,10) = 14,67 (тыс. рублей)

Ответ : цена ноутбука составляет 14,67 тыс. рублей.

Задача 8 . В прошлом месяце цена ноутбука составляла 21 тыс. рублей. В этом месяце цена повысилась до 22,05 тыс. рублей. На сколько процентов повысилась цена?

Решение

Определим насколько рублей повысилась цена

22,05 − 21 = 1,05 (тыс. руб)

Узнаем какую часть 1,05 тыс. руб. составляет от 21 тыс. руб.

Выразим полученный результат в процентах

0,05 × 100 = 5%

Ответ : цена ноутбука повысилась на 5%

Задача 8 . Рабочий должен был изготовить по плану 600 деталей, а он изготовил 900 деталей. На сколько процентов он выполнил план?

Решение

Узнаем во сколько раз 900 деталей больше, чем 600 деталей. Для этого найдем отношение 900 к 600

Значение данной дроби равно 1,5. Выразим это значение в процентах:

1,5 × 100 = 150%

Значит, рабочий выполнил план на 150%. То есть выполнил его на все 100%, изготовив 600 деталей. Затем изготовил еще 300 деталей, что составляет 50% от изначального плана.

Ответ : рабочий выполнил план на 150%.

Сравнение величин в процентах

Мы уже много раз сравнивали величины различными способами. Первым нашим инструментом была разность. Так, к примеру чтобы сравнить 5 рублей и 3 рубля, мы записывали разность 5−3. Получив ответ 2, можно было сказать, что «пять рублей больше трех рублей на два рубля».

Получаемый в результате вычитания ответ в повседневной жизни называют не «разностью», а «разницей».

Так, разница между пятью и тремя рубля составляет два рубля.

Следующим инструментом, которым мы воспользовались для сравнения величин, было отношение. Отношение позволяло нам узнать во сколько раз первое число больше второго (или сколько раз первое число содержит второе).

Так, к примеру десять яблок больше двух яблок в пять раз. Или по другому, десять яблок содержит два яблока пять раз. Данное сравнение можно записать с помощью отношения

Но величины можно сравнить и в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах.

Для сравнения величин в процентах, одну из них нужно обозначить как 100%, а вторую исходя из условий задачи.

Например, узнаем на сколько процентов десять яблок больше, чем восемь яблок.

За 100% нужно обозначить ту величину с которой мы что-либо сравниваем. Мы сравниваем 10 яблок с 8 яблоками. Значит, за 100% обозначаем 8 яблок:

Теперь наша задача сравнить на сколько процентов 10 яблок больше, чем эти 8 яблок. 10 яблок это 8+2 яблока. Значит, добавив к восьми яблокам ещё два яблока, мы увеличим 100% еще на какое-то число процентов. Чтобы узнать на какое именно, определим сколько процентов от восьми яблок составляют два яблока

Добавив эти 25% к восьми яблокам, мы получим 10 яблок. А 10 яблок это 8+2, то есть 100% и еще 25%. Итого получаем 125%

Значит, десять яблок больше восьми яблок на 25%.

Теперь решим обратную задачу. Узнаем насколько процентов восемь яблок меньше, чем десять яблок. Сразу напрашивается ответ, что восемь яблок меньше на 25%. Однако это не так.

Мы сравниваем восемь яблок с десятью яблоками. Мы договорились, что за 100% будем брать то, с чем сравниваем. Поэтому в этот раз за 100% берем 10 яблок:

Восемь яблок это 10−2, то есть уменьшив 10 яблок на 2 яблока, мы уменьшим их на какое-то число процентов. Чтобы узнать на какое именно, определим сколько процентов от десяти яблок составляют два яблока

Отняв эти 20% от десяти яблок, мы получим 8 яблок. А 8 яблок это 10−2, то есть 100% и минус 20%. Итого получаем 80%

Значит, восемь яблок меньше десяти яблок на 20%.

Задача 2 . На сколько процентов 5000 рублей больше, чем 4000 рублей?

Решение

Примем 4000 рублей за 100%. 5 тысяч больше 4 тысяч на 1 тысячу. Значит, увеличив четыре тысячи на одну тысячу, мы увеличим четыре тысячи на какое-то количество процентов. Узнаем на какое именно. Для этого определим какую часть одна тысяча составляет от четырех тысяч:

Выразим полученный результат в процентах:

0,25 × 100 = 25%

1000 рублей от 4000 рублей составляют 25%. Если прибавить эти 25% к 4000, то получится 5000 рублей. Значит, 5000 рублей на 25% больше, чем 4000 рублей

Задача 3 . На сколько процентов 4000 рублей меньше, чем 5000 рублей?

В этот раз сравниваем 4000 с 5000. Примем 5000 за 100%. Пять тысяч больше четырех тысяч на одну тысячу рублей. Узнаем какую часть одна тысяча составляет от пяти тысяч

Тысяча от пяти тысяч составляет 20%. Если вычесть эти 20% от 5000 рублей, то получим 4000 рублей.

Значит, 4000 рублей меньше 5000 рублей на 20%

Задачи на концентрацию, сплавы и смеси

Допустим, возникло желание приготовить какой-нибудь сок. У нас в распоряжении имеется вода и малиновый сироп

Нальем 200 мл воды в стакан:

Добавим 50 мл малинового сиропа и размешаем полученную жидкость. В результате у нас получится 250 мл малинового сока (200 мл воды + 50 мл сиропа = 250 мл сока)

Какую часть от получившегося сока составляет малиновый сироп?

Малиновый сироп составляет сока. Вычислим это отношение, получим число 0,20 . Это число показывает количество растворённого сиропа в получившемся соке. Назовём это число концентрацией сиропа .

Концентрацией растворённого вещества называют отношение количества растворённого вещества или его массы к объему раствора.

Концентрация обычно выражается в процентах. Давайте выразим концентрацию сиропа в процентах:

0,20 × 100 = 20%

Таким образом, концентрация сиропа в малиновом соке составляет 20%.

Вещества в растворе могут быть неоднородными. Например, смешаем 3 л воды и 200 г соли.

Масса 1 л воды составляет 1 кг. Тогда масса 3 л воды будет составлять 3 кг. Переведем 3 кг в граммы, получим 3 кг = 3000 г.

Теперь в 3000 г воды опустим 200 г соли и смешаем полученную жидкость. В результате получится соленный раствор, общая масса которого будет составлять 3000+200, то есть 3200 г. Найдем концентрацию соли в полученном растворе. Для этого найдём отношение массы растворенной соли к массе раствора

Значит, при смешивании 3 л воды и 200 г соли получится 6,25%-й раствор соли.

Аналогично может быть определено количество вещества в сплаве или в смеси. Например, сплав содержит олово массой 210 г, и серебро массой 90 г. Тогда масса сплава будет составлять 210+90, то есть 300 г. Олова в сплаве будет содержаться , а серебра . В процентном соотношении олова будет 70% , а серебра 30%

При смешивании двух растворов получается новый раствор, состоящий из первого и второго растворов. У нового раствора концентрация вещества может быть другой. Полезным навыком является умение решать задачи на концентрацию, сплавы и смеси. В общем итоге смысл таких задач заключается в отслеживании изменений, которые происходят при смешивании растворов различной концентрации.

Смешаем два малиновых сока. Первый сок объемом 250 мл содержит 12,8% малинового сиропа. А второй сок объемом 300 мл содержит 15% малинового сиропа. Сольем эти два сока в большой стакан и смешаем. В результате получим новый сок объемом 550 мл.

Теперь определим концентрацию сиропа в полученном соке. Первый слитый сок объемом 250 мл содержал 12,8% сиропа. А 12,8% от 250 мл это 32 мл. Значит, первый сок содержал 32 мл сиропа.

Второй слитый сок объемом 300 мл содержал 15% сиропа. А 15% от 300 мл это 45 мл. Значит, второй сок содержал 45 мл сиропа.

Сложим количества сиропов:

32 мл + 45 мл = 77 мл

Эти 77 мл сиропа содержатся в новом соке, объем которого составляет 550 мл. Определим концентрацию сиропа в этом соке. Для этого найдём отношение 77 мл растворённого сиропа к объему сока 550 мл:

Значит, при смешивании 12,8%-го малинового сока объемом 250 мл и 15%‍-го малинового сока объемом 300 мл, получается 14%-й малиновый сок объемом 550 мл.

Задача 1 . Имеются 3 раствора морской соли в воде: первый раствор содержит 10% соли, второй содержит 15% соли и третий — 20% соли. Смешали 130 мл первого раствора, 200 мл второго раствора и 170 мл третьего раствора. Определите сколько процентов составляет морская соль в полученном растворе.

Решение

Определим объем полученного раствора:

130 мл + 200 мл + 170 мл = 500 мл

Поскольку в первом растворе было 130 × 0,10 = 13 мл морской соли, во втором растворе 200 × 0,15 = 30 мл морской соли, а в третьем — 170 × 0,20 = 34 мл морской соли, то в полученном растворе будет содержаться 13 + 30 + 34 = 77 мл морской соли.

Определим концентрацию морской соли в полученном растворе. Для этого найдём отношение 77 мл морской соли к объему раствора 500 мл

Значит, в полученном растворе содержится 15,4% морской соли.

Задача 2 . Сколько граммов воды надо добавить к 50 г раствора, содержащего 8% соли, чтобы получить 5%-й раствор?

Решение

Заметим, что если к имеющемуся раствору добавить воды, то количество соли в нём не изменится. Изменится только её процентное содержание, поскольку добавление воды в раствор приведёт к изменению его массы.

Нам нужно добавить такое количество воды при котором восемь процентов соли стали бы пятью процентами.

Определим сколько граммов соли содержится в 50 г раствора. Для этого найдем 8% от 50

50 г × 0,08 = 4 г

8% от 50 г составляют 4 г. Другими словами, на восемь частей из ста приходятся 4 грамма соли. Давайте сделаем так, чтобы эти 4 грамма приходились не на восемь частей, а на пять частей, то есть на 5%

4 грамма — 5%

Теперь зная, что на 5% раствора приходятся 4 грамма, мы можем найти массу всего раствора. Для этого нужно :

4 г: 5 = 0,8 г
0,8 г × 100 = 80 г

80 граммов раствора это масса при которой 4 грамма соли будут приходиться на 5% раствора. А для получения этих 80 граммов, нужно к изначальным 50 граммам добавить 30 граммов воды.

Значит, для получения 5%-го раствора соли, нужно к имеющемуся раствору добавить 30 г воды.

Задача 2 . Виноград содержит 91% влаги, а изюм – 7%. Сколько килограммов винограда требуется для получения 21 килограмма изюма?

Решение

Виноград состоит из влаги и чистого вещества. Если в свежем винограде содержится 91% влаги, то на остальные 9% будет приходиться чистое вещество этого винограда:

Изюм же содержит 93% чистого вещества и 7% влаги:

Заметим, что в процессе превращения винограда в изюм, исчезает только влага этого винограда. Чистое вещество остаётся без изменения. После того, как виноград превратится в изюм, в получившемся изюме будет 7% влаги и 93% чистого вещества.

Определим сколько чистого вещества содержится в 21 кг изюма. Для этого найдем 93% от 21 кг

21 кг × 0,93 = 19,53 кг

Теперь вернемся к первому рисунку. Наша задача состояла в том, чтобы определить сколько винограда нужно взять для получения 21 кг изюма. Чистое вещество массой 19,53 кг будет приходиться на 9% винограда:

Теперь зная, что 9% чистого вещества составляют 19,53 кг, мы можем определить сколько винограда требуется для получения 21 кг изюма. Для этого нужно найти число по его проценту:

19,53 кг: 9 = 2,17 кг
2,17 кг × 100 = 217 кг

Значит, для получения 21 кг изюма нужно взять 217 кг винограда.

Задача 3 . В сплаве олова и меди медь составляет 85%. Сколько надо взять сплава, чтобы в нём содержалось 4,5 кг олова?

Решение

Если в сплаве медь составляет 85%, то на остальные 15% будет приходиться олово:

Спрашивается сколько надо взять сплава, чтобы в нем содержалось 4,5 олова. Поскольку олова в сплаве содержится 15%, то 4,5 кг олова и будут приходиться на эти 15%.

А зная, что 4,5 кг сплава составляют 15% мы можем определить массу всего сплава. Для этого нужно найти число по его проценту:

4,5 кг: 15 = 0,3 кг
0,3 кг × 100 = 30 кг

Значит, сплава нужно взять 30 кг, чтобы в нём содержалось 4,5 кг олова.

Задача 4 . Смешали некоторое количество 12%-го раствора соляной кислоты с таким же количеством 20%-го раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.

Решение

Изобразим на рисунке первый раствор в виде прямой линии и выделим на нём 12%

Поскольку количество растворов одинаково, рядом можно изобразить такой же рисунок, иллюстрирующий второй раствор с содержанием соляной кислоты 20%

У нас получилось двести частей раствора (100% + 100%) , тридцать две части из которых составляют соляную кислоту (12% + 20%)

Определим какую часть 32 части составляют от 200 частей

Значит, при смешивании 12%-го раствора соляной кислоты с таким же количеством 20%-го раствора этой же кислоты получится 16%-й раствор соляной кислоты.

Для проверки представим, что масса первого раствора была 2 кг. Масса второго раствора так же будет составлять 2 кг. Тогда при смешивании этих растворов получится 4 кг раствора. В первом растворе соляной кислоты было 2 × 0,12 = 0,24 кг, а во втором — 2 × 0,20 = 0,40 кг . Тогда в новом растворе соляной кислоты будет 0,24 + 0,40 = 0,64 кг . Концентрация соляной кислоты составит 16%

Задачи для самостоятельного решения

на , мы найдем 60% от числа

Теперь увеличим число на найденные 60%, т.е. на число

Ответ: новое значение равно

Задача 12. Ответьте на следующие вопросы:

1) Потратили 80 % суммы. Сколько процентов этой суммы осталось?
2) Мужчины составляют 75 % всех работников завода. Сколько процентов работников завода составляют женщины?
3) Девочки составляют 40 % класса. Сколько процентов класса составляют мальчики?

А Решение

Воспользуемся переменной. Пусть P это исходное число о котором говорится в задаче. Примем это исходное число P за 100%

Уменьшим это исходное число P на 50%

Теперь новое число составляет 50% от исходного числа. Узнаем во сколько раз исходное число P больше нового числа. Для этого найдем отношение 100% к 50%

Исходное число в два раза больше нового. Это видно даже по рисунку. А чтобы сделать новое число равным исходному, его нужно увеличить в два раза. А увеличить число в два раза означает увеличить его на 100%.

Значит, новое число, которое составляет половину от исходного числа, нужно увеличить на 100%.

Рассматривая новое число, его также принимают за 100%. Так, на приведенном рисунке новое число является половиной от исходного числа и подписано как 50%. По отношению к исходному числу новое число является половиной. Но если рассматривать его отдельно от исходного, его нужно принимать за 100%.

Поэтому на рисунке, новое число которое изображается линией, сначала было обозначено как 50%. Но затем это число мы обозначили как 100%.

Ответ: чтобы получить исходное число, новое число надо увеличить на 100%.

Задача 16. В прошлом месяце в городе произошло 15 ДТП.
В этом месяце этот показатель снизился до 6. На сколько процентов снизилось количество ДТП?

Решение

В прошлом месяце было 15 ДТП. В этом месяце 6. Значит, количество ДТП снизилось на 9.
Примем 15 ДТП за 100%. Снизив 15 ДТП на 9, мы снизим их на какое-то число процентов. Чтобы узнать на какое именно, узнаем какую часть 9 ДТП составляет от 15 ДТП

Ответ: концентрация получившегося раствора составляет 12%.

Задача 18. Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 19% раствора этого же вещества. Найдите концентрацию получившегося раствора.

Решение

Масса обоих растворов одинакова. Каждый раствор можно принять за 100%. После сложения растворов получится 200% раствора. В первом растворе было 11% вещества, а во втором 19% вещества. Тогда в получившемся 200%-м растворе будет 11% + 19% = 30% вещества.

Определим концентрацию получившегося растворе. Для этого узнаем какую часть тридцать частей вещества составляют от двухсот частей вещества:

1,10. Значит, цена за первый месяц станет 1,10 .

За второй месяц цена также повысилась на 10% . Прибавим к нынешней цене 1,10 десять процентов от этой цены, получим 1,10 + 0,10 × 1,10 . Эта сумма равна выражению 1,21 . Значит, цена за второй месяц станет 1,21 .

За третий месяц цена также повысилась на 10% . Прибавим к нынешней цене 1,21 десять процентов от этой цены, получим 1,21 + 0,10 × 1,21. Эта сумма равна выражению 1,331 . Тогда цена за третий месяц станет 1,331 .

Вычислим разницу между новой и старой ценой. Если изначальная цена была равна 1 , то повысилась она на 1,331 − 1 = 0,331 . Выразим этот результат в процентах, получим 0,331 × 100 = 33,1%

Ответ: за 3 месяца цены на продукты питания повысились на 33,1%.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках