Vektör. Temel özellikler

Tanım Sıralı bir koleksiyona (x 1, x 2, ..., x n) n gerçek sayı denir n-boyutlu vektör, ve x i (i = 1, ..., n) sayıları bileşenler veya koordinatlar,

Örnek. Örneğin, belirli bir otomobil fabrikasının vardiya başına 50 araba, 100 kamyon, 10 otobüs, 50 takım araba yedek parça ve 150 takım kamyon ve otobüs üretmesi gerekiyorsa, bu fabrikanın üretim programı şu şekilde yazılabilir: beş bileşene sahip bir vektörün (50, 100 , 10, 50, 150) formu.

Notasyon. Vektörler, kalın küçük harflerle veya üstte bir çubuk veya ok bulunan harflerle gösterilir, örneğin, a veya . iki vektör denir eşit aynı sayıda bileşene sahiplerse ve karşılık gelen bileşenleri eşitse.

Vektör bileşenleri değiştirilemez, örneğin (3, 2, 5, 0, 1) ve (2, 3, 5, 0, 1) farklı vektörlerdir.
Vektörler üzerinde işlemler.Ürüne görex= (x 1, x 2, ..., x n) λ gerçel sayısına göre λ vektörü denir x= (λ x 1, λ x 2, ..., λ x n).

Toplamx= (x 1, x 2, ..., xn) ve y= (y 1, y 2, ..., y n) vektörü olarak adlandırılır x + y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

Vektörlerin uzayı. n-boyutlu vektör uzayı r n, gerçek sayılarla çarpma ve toplama işlemlerinin tanımlandığı tüm n boyutlu vektörlerin kümesi olarak tanımlanır.

Ekonomik illüstrasyon. n-boyutlu vektör uzayının ekonomik gösterimi: mal alanı (mal). Altında emtia belli bir yerde belli bir zamanda satışa çıkan bazı mal veya hizmetleri anlayacağız. Elinizde sonlu sayıda öğe olduğunu varsayalım, n; tüketici tarafından satın alınan her birinin miktarları bir dizi mal ile karakterize edilir.

x= (x 1, x 2, ..., xn),

burada x i, tüketici tarafından satın alınan i-inci malın miktarını gösterir. Tüm malların keyfi bölünebilme özelliğine sahip olduğunu varsayacağız, böylece her birinin negatif olmayan herhangi bir miktarı satın alınabilir. O zaman tüm olası mal kümeleri, mal uzayının vektörleridir C = ( x= (x 1, x 2, ..., x n) x ben ≥ 0, ben = 1, ..., n).

Doğrusal bağımsızlık. sistem e 1 , e 2 , ... , e m n boyutlu vektörler denir lineer bağımlıλ 1, λ 2, ..., λ m sayıları varsa, bunlardan en az biri sıfırdan farklı olacak şekilde λ 1 e 1 + λm e m = 0; aksi takdirde, bu vektör sistemine denir Doğrusal bağımsız, yani, belirtilen eşitlik yalnızca tüm λ 1 = λ 2 = ... = λ m = 0 olduğunda mümkündür. Vektörlerin doğrusal bağımlılığının geometrik anlamı r 3 yönlendirilmiş segmentler olarak yorumlanarak aşağıdaki teoremleri açıklayınız.

Teorem 1. Bir vektörden oluşan bir sistem, ancak ve ancak bu vektör sıfır ise lineer bağımlıdır.

Teorem 2. İki vektörün lineer bağımlı olması için lineer (paralel) olmaları gerekli ve yeterlidir.

teorem 3 ... Üç vektörün lineer bağımlı olabilmesi için aynı düzlemde olmaları (aynı düzlemde olmaları) gerekli ve yeterlidir.

Vektörlerin sol ve sağ üçlüleri. Üç düzlemsel olmayan vektör a, b, c aranan sağ gözlemci, ortak kökenlerinden vektörlerin uçlarını geçerse a, b, c gösterilen sırada, saat yönünde görünüyor. Aksi halde a, b, c -sol üçlü... Vektörlerin tüm sağ (veya sol) üçlülerine denir eşit olarak odaklı.

Temel ve koordinatlar. Troyka e 1, e 2 , e 3 eş düzlemli olmayan vektör r 3 denir temel, ve vektörlerin kendileri e 1, e 2 , e 3 - temel... herhangi bir vektör a temel vektörler cinsinden benzersiz bir şekilde genişletilebilir, yani şu şekilde temsil edilir

a= x 1 e 1 + x 2 e 2 + x 3 e 3, (1.1)

açılımında (1.1) x 1, x 2, x 3 sayılarına denir koordinatlara temelde e 1, e 2 , e 3 ve belirtilir a(x 1, x 2, x 3).

Ortonormal taban. vektörler ise e 1, e 2 , e 3 çift diktir ve her birinin uzunluğu bire eşittir, o zaman taban denir ortonormal, ve koordinatlar x 1, x 2, x 3 - dikdörtgen. Ortonormal tabanın temel vektörleri ile gösterilecektir. ben, j, k.

uzayda olduğunu varsayacağız r 3 Kartezyen dikdörtgen koordinatlarının doğru sistemi seçilir (0, ben, j, k}.

Vektör ürün.vektör ürüna vektör başına B vektör denir C, aşağıdaki üç koşul tarafından belirlenir:

1. Vektör uzunluğu C vektörler üzerine kurulmuş bir paralelkenarın alanına sayısal olarak eşittir a ve B, yani
C= | bir || b | günah ( a^B).

2. Vektör C vektörlerin her birine dik a ve B.

3. Vektörler a, B ve C belirtilen sırada alınan bir sağ üçlü oluşturur.

vektör ürün için C notasyon tanıtıldı c =[ab] veya
c = bir × B.

vektörler ise a ve B doğrusal, sonra günah ( bir ^ b) = 0 ve [ ab] = 0, özellikle, [ aa] = 0. Birim vektörlerin vektör ürünleri: [ ij]=k, [jk] = ben, [ki]=J.

vektörler ise a ve B temelinde verilen ben, j, k koordinatlar a(a 1, 2, a 3), B(b 1, b 2, b 3), sonra

Karışık iş. İki vektörün çapraz çarpımı ise a ve Büçüncü vektörle çarpılan skaler C, o zaman üç vektörün böyle bir ürününe denir karışık iş ve sembolü ile gösterilir a M.Ö.

vektörler ise bir, b ve C temelde ben, j, k koordinatları tarafından verilen
a(a 1, 2, a 3), B(b 1, b 2, b 3), C(c 1, c 2, c 3), sonra

.

Karışık ürünün basit bir geometrik yorumu vardır - bu üç vektör üzerine inşa edilmiş bir paralel borunun hacmine mutlak değerde eşit bir skalerdir.

Vektörler bir sağ üçlü oluşturuyorsa, bunların karışık çarpımı, belirtilen hacme eşit pozitif bir sayıdır; eğer üç a, b, c - sol, o zaman bir bc<0 и V = - bir bc, bu nedenle V = | bir b c |.

Birinci bölümdeki problemlerde karşılaşılan vektörlerin koordinatlarının sağ ortonormal tabana göre verildiği varsayılmıştır. Birim vektörden vektöre eş yönlü a, sembolü ile gösterilir aÖ. sembol r=OM M noktasının yarıçap vektörü ile gösterilir, semboller a, AB veya |a |, |AB | vektör modülleri a ve AB.

Örnek 1.2. Vektörler arasındaki açıyı bulun a= 2m+4n ve B= m-n, nerede m ve n - birim vektörler ve arasındaki açı m ve n 120 p'ye eşittir.

Çözüm... elimizde: çünkü φ = ab/ ab, ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2milyon=
= 2 - 4 + 2cos120 o = - 2 + 2 (-0,5) = -3; bir = ; a 2 = (2m+4n) (2m+4n) =
= 4m 2 +16milyon+16n 2 = 4 + 16 (-0,5) + 16 = 12, yani a =. b = ; B 2 =
= (m-n)(m-n) = m 2 -2milyon+n 2 = 1-2 (-0,5) +1 = 3, yani b =. Son olarak, elimizde: cos φ == -1/2, φ = 120 o.

Örnek 1.3. vektörleri bilmek AB(-3, -2.6) ve M.Ö(-2,4,4), ABC üçgeninin AD yüksekliğinin uzunluğunu hesaplayın.

Çözüm... ABC üçgeninin alanını S ile göstererek, şunu elde ederiz:
S = 1/2 M.Ö. O zaman AD = 2S / BC, BC = = = 6,
S = 1/2 | AB ×klima |. AC = AB + M.Ö., yani vektör AC koordinatları var
.

TANIM

Vektör(lat. " vektör"-" yatak ") - uzayda veya bir düzlemde düz bir çizginin yönlendirilmiş bir parçası.

Grafiksel olarak, bir vektör, belirli bir uzunlukta yönlendirilmiş bir çizgi parçası olarak tasvir edilir. Başı bir noktada ve sonu bir noktada olan bir vektör (Şekil 1) olarak gösterilir. Ayrıca, bir vektör, örneğin küçük bir harfle gösterilebilir.

Uzayda bir koordinat sistemi belirtilirse, vektör bir dizi koordinat tarafından benzersiz bir şekilde belirtilebilir. Yani vektör, büyüklüğü (uzunluğu), yönü ve uygulama noktası (vektörün başlangıcı) olan bir nesne olarak anlaşılır.

Vektör hesabının başlangıcı, 1831'de Alman matematikçi, mekanik, fizikçi, astronom ve araştırmacı Johann Karl Friedrich Gauss'un (1777-1855) eserlerinde ortaya çıktı. Vektörlerle işlemler üzerine makaleler İrlandalı matematikçi, mekanik ve teorik fizikçi Sir William Rowan Hamilton (1805-1865) tarafından kuaterniyon hesabı çerçevesinde yayınlandı. Bilim adamı "vektör" terimini önerdi ve vektörler üzerinde bazı işlemleri tanımladı. Vektör hesabı, İngiliz fizikçi, matematikçi ve mekanik James Clerk Maxwell'in (1831-1879) elektromanyetizma üzerindeki çalışmaları sayesinde daha da geliştirildi. 1880'lerde Amerikalı fizikçi, fizik kimyager, matematikçi ve mekanik Josiah Willard Gibbs (1839-1903) tarafından "Elements of Vector Analysis" kitabı yayınlandı. Modern vektör analizi, 1903 yılında kendi kendini yetiştirmiş İngiliz bilim adamı, mühendis, matematikçi ve fizikçi Oliver Heaviside (1850-1925) tarafından tanımlanmıştır.

TANIM

Uzunluk veya vektör modülü vektörü tanımlayan yönlendirilmiş parçanın uzunluğudur. Olarak belirtilir.

Temel vektör türleri

sıfır vektör başlangıç ​​noktası ve bitiş noktası çakışan bir vektördür. Sıfır vektörünün uzunluğu sıfırdır.

Bir doğruya paralel olan veya bir doğru üzerinde bulunan vektörlere denir. doğrusal(incir. 2).

birlikte yönetilen eğer yönleri aynıysa.

Şekil 2'de bunlar vektörler ve. Vektörlerin eş yönlülüğü şu şekilde gösterilir:

İki eşdoğrusal vektör denir zıt yönlü yönleri ters ise.

Şekil 3'te bunlar vektörler ve. Tanım:.

VEKTÖRLER... HAREKETLERÜSTÜNDEVEKTÖRLER. SKALAR,

VEKTÖR, VEKTÖRLERİN KARIŞIK ÜRÜNÜ.

1. VEKTÖRLER, VEKTÖRLER ÜZERİNDEKİ EYLEMLER.

Temel tanımlar.

Tanım 1. Seçilen birim sistemindeki sayısal değeri ile tam olarak karakterize edilen bir niceliğe denir. skaler veya skaler .

(Vücut ağırlığı, hacim, süre vb.)

Tanım 2. Sayısal bir değer ve yön ile karakterize edilen bir niceliğe denir. vektör veya vektör .

(Deplasman, güç, hız vb.)

Tanımlamalar: veya,.

Geometrik bir vektör, yönlü bir çizgidir.

Bir vektör için - bir nokta A- başlangıç ​​noktası V- vektörün sonu.

Tanım 3.Modül vektör AB doğru parçasının uzunluğudur.

Tanım 4. Modülü sıfıra eşit olan vektöre denir. sıfır , ile belirtilir.

Tanım 5. Paralel doğrular veya bir doğru üzerinde bulunan vektörlere denir. doğrusal ... İki doğrusal vektör aynı yöne sahipse, bunlara denir. birlikte yönetilen .

Tanım 6.İki vektör kabul edilir eşit , Eğer onlar birlikte yönetilen ve mutlak değerde eşittir.

Vektörler üzerinde eylemler.

1) Vektörlerin eklenmesi.

tanım 6.Toplam iki vektör ve uygulamalarının ortak noktasından başlayarak bu vektörler üzerine kurulan paralelkenarın köşegenidir. (paralelkenar kuralı).

1.

tanım 7.Üç vektörün toplamına, bu vektörler üzerine kurulan paralelyüzün köşegeni denir. (kutu kuralı).

tanım sekiz. Eğer A, V, İLE BİRLİKTE - keyfi noktalar, ardından + = (üçgen kuralı).

incir. 2

Ekleme özellikleri.

1 Ö . + = + (transpozisyon yasası).

2 Ö . + (+) = (+) + = (+) + (kombinasyon yasası).

3 Ö . + (– ) + .

2) Vektörlerin çıkarılması.

tanım dokuz. Altında fark vektörler ve anlama vektörü = - öyle ki + = .

Paralelkenarda, bu başka diyagonal SD (bkz. Şekil 1).

3) Bir vektörü bir sayı ile çarpmak.

tanım on. Ürüne göre skaler başına vektörler k vektör denir

= k = k ,

uzun ka , ve yönü:

1. vektörün yönü ile çakışıyorsa k > 0;

2. Vektörün yönünün tersi ise, k < 0;

3. keyfi olarak k = 0.

Bir vektörü bir sayı ile çarpmanın özellikleri.

1 Ö . (k + ben ) = k + ben .

k ( + ) = k + k .

2 Ö . k (ben ) = (kl ) .

3 Ö . 1  = , (–1)  = – , 0  = .

Vektör özellikleri.

tanım on bir.İki vektör ve denir doğrusal üzerinde yer alırlarsa paralel çizgiler veya bir düz çizgi.

Boş bir vektör, herhangi bir vektörle eşdoğrusaldır.

Teorem 1. Sıfır olmayan iki vektör ve doğrusal,  orantılı olduklarında, yani.

= k , k bir skalerdir.

tanım 12.Üç vektör, denir aynı düzlemde bir düzleme paralellerse veya içinde yatıyorlarsa.

Teorem 2.Üç sıfır olmayan vektör, aynı düzlemde,  bunlardan biri diğer ikisinin lineer bir kombinasyonu olduğunda, yani.

= k + ben , k , ben - skaler.

Vektörün eksene izdüşümü.

Teorem 3. Bir vektörün bir eksene izdüşümü (yönlendirilmiş düz çizgi) ben vektörün uzunluğunun ürününe ve vektörün yönü ile eksen yönü arasındaki açının kosinüsüne eşittir, yani. = a  C işletim sistemi  ,  = ( , ben).

2. VEKTÖR KOORDİNATLARI

tanım 13. Koordinat eksenlerinde vektör projeksiyonları Ah, kuruluş birimi, Oz arandı vektör koordinatları. Tanım:  a x , a y , a z .

Vektör uzunluğu:

Örnek: Vektörün uzunluğunu hesaplayın.

Çözüm:

Noktalar arasındaki mesafe ve formülle hesaplanır: .

Örnek: M (2,3, -1) ve K (4,5,2) noktaları arasındaki mesafeyi bulun.

Koordinat biçiminde vektörler üzerindeki eylemler.

Verilen vektörler =  a x , a y , a z ve =  B x , B y , B z .

1. (  )= a x  B x , a y  B y , a z  B z .

2.  =   a x ,  a y ,  a z, nerede  bir skalerdir.

Vektörlerin nokta çarpımı.

Tanım:İki vektörün nokta çarpımı altında ve

bu vektörlerin uzunluklarının, aralarındaki açının kosinüsü ile çarpımına eşit bir sayı olarak anlaşılır, yani. = , vektörler ve arasındaki açıdır.

Nokta ürün özellikleri:

1.  =

2. ( + ) =

3.

4.

5. , skaler nerede.

6.iki vektör diktir (ortogonal), eğer .

7.if ve sadece eğer .

Koordinat biçimindeki nokta çarpımı: , Nerede ve .

Örnek: Vektörlerin nokta çarpımını bulun ve

Çözüm:

Vektör tutan vektörler.

Tanım: İki vektörün vektör çarpımı, aşağıdakiler için bir vektör olarak anlaşılır:

Modül, bu vektörler üzerine inşa edilen paralelkenarın alanına eşittir, yani. , vektörler arasındaki açı ve

Bu vektör, çarpılmakta olan vektörlere diktir, yani.

Vektörler eşdoğrusal değilse, o zaman sağ vektör üçlüsünü oluştururlar.

Vektör ürün özellikleri:

(1) Faktörlerin sırası değiştirildiğinde, vektör çarpımı modülünü koruyarak işaretini tersine değiştirir, yani.

2 .Vektör karesi sıfır vektörüne eşittir, yani.

3 Skaler faktör vektör ürününün işaretinin dışına taşınabilir, yani.

4 Herhangi üç vektör için eşitlik

5 İki vektörün doğrusallığı için gerekli ve yeterli bir koşul ve:

Koordinat biçiminde vektör ürünü.

Vektörlerin koordinatları ve , daha sonra çapraz ürünleri aşağıdaki formülle bulunur:

.

Daha sonra bir vektör ürününün tanımından, vektörler üzerine kurulu bir paralelkenarın alanının aşağıdaki formülle hesaplandığını takip eder:

Örnek: Köşeleri (1; -1; 2), (5; -6; 2), (1; 3; -1) olan bir üçgenin alanını hesaplayın.

Çözüm: .

Daha sonra ABC üçgeninin alanı aşağıdaki gibi hesaplanacaktır:

,

Vektörlerin karışık çarpımı.

Tanım: Vektörlerin karışık (vektör-skaler) çarpımı, aşağıdaki formülle belirlenen bir sayıdır: .

Karışık çalışma özellikleri:

1. Karışık ürün, faktörlerinin döngüsel permütasyonu altında değişmez, yani. .

2. İki bitişik faktörün permütasyonu üzerine, karışık ürün işaretini tersine değiştirir, yani. ...

3 Üç vektörün eş düzlemliliği için gerekli ve yeterli bir koşul : =0.

4 Üç vektörün karışık ürünü, bu vektörler üzerinde inşa edilen paralelyüzün hacmine eşittir, bu vektörler sağ üçlü oluşturuyorsa artı işaretiyle, sol üçlü oluşturuyorsa eksi işaretiyle alınır, yani. .

biliniyorsa koordinatlar vektörler , daha sonra karma iş şu formülle bulunur:

Örnek: Vektörlerin karışık çarpımını hesaplayın.

Çözüm:

3. Vektör sisteminin temeli.

Tanım. Bir vektör sistemi, aynı uzaya ait birkaç vektör olarak anlaşılır. r.

Yorum Yap. Sistem sonlu sayıda vektörden oluşuyorsa, bunlar farklı indekslerle aynı harfle gösterilir.

Örnek.

Tanım. Formun herhangi bir vektörü = vektörlerin lineer kombinasyonu olarak adlandırılır. Sayılar lineer kombinasyonun katsayılarıdır.

Örnek. .

Tanım... Vektör, vektörlerin doğrusal bir birleşimiyse , o zaman vektörün vektörler cinsinden doğrusal olarak ifade edildiği söylenir. .

Tanım. vektör sistemi denir Doğrusal bağımsız sistemin vektörlerinden hiçbiri diğer vektörlerin lineer bir kombinasyonu gibi olamazsa. Aksi takdirde, sistem lineer bağımlı olarak adlandırılır.

Örnek... vektör sistemi vektörden beri lineer bağımlı .

Temelin belirlenmesi. Bir vektör sistemi aşağıdaki durumlarda bir temel oluşturur:

1) lineer bağımsızdır,

2) herhangi bir uzay vektörü, onun içinden doğrusal olarak ifade edilir.

Örnek 1. Uzay temeli:.

2. vektörler sisteminde vektörler temeldir: vektörler cinsinden doğrusal olarak ifade edilir.

Yorum Yap. Belirli bir vektör sisteminin temelini bulmak için yapmanız gerekenler:

1) vektörlerin koordinatlarını matrise yazın,

2) matrisi üçgen bir forma getirmek için temel dönüşümleri kullanmak,

3) matrisin sıfır olmayan satırları sistemin temeli olacaktır,

4) tabandaki vektörlerin sayısı matrisin rankına eşittir.

için görevler olacak bağımsız karar hangi cevapları görebilirsiniz.

vektör kavramı

Vektörler ve üzerlerindeki işlemler hakkında her şeyi öğrenmeden önce, basit bir problemi çözmeye başlayın. Girişimciliğinizin bir vektörü ve yenilikçi yeteneklerinizin bir vektörü vardır. Girişimcilik vektörü sizi Hedef 1'e ve yenilikçi yeteneklerin vektörü Hedef 2'ye götürür. Oyunun kuralları öyledir ki, bu iki vektörün yönünde aynı anda hareket edemezsiniz ve aynı anda iki hedefe ulaşamazsınız. Vektörler etkileşime girer veya matematiksel olarak vektörler üzerinde bazı işlemler yapılır. Bu işlemin sonucu, sizi Hedef 3'e götüren "Sonuç" vektörüdür.

Şimdi söyle bana: "İşletme" ve "Yenilikçi yetenekler" vektörleri üzerindeki hangi işlemin sonucu "Sonuç" vektörüdür? Hemen söyleyemiyorsanız, cesaretiniz kırılmasın. Bu derste ilerledikçe, bu soruyu cevaplayabileceksiniz.

Yukarıda zaten gördüğümüz gibi, vektör mutlaka bir noktadan gider. A bir noktaya kadar düz bir çizgide B... Bu nedenle, her vektörün yalnızca sayısal bir değeri - uzunluk değil, aynı zamanda fiziksel ve geometrik - yönlülük vardır. Bu, bir vektörün ilk ve en basit tanımına götürür. Yani vektör, bir noktadan giden yönlendirilmiş bir doğru parçasıdır. A diyeceğim şey şu ki B... Aşağıdaki gibi belirlenmiştir:.

Ve farklı başlamak için vektör işlemleri , bir vektör tanımıyla daha tanışmamız gerekiyor.

Vektör, bir başlangıç ​​noktasından varmak istediğiniz noktanın bir tür temsilidir. Örneğin, üç boyutlu bir vektör genellikle şu şekilde yazılır: (x, y, z) . Oldukça basit, bu sayılar bir noktaya ulaşmak için üç farklı yönde ne kadar yol kat edilmesi gerektiğini gösterir.

Bir vektör verilsin. nerede x = 3 (sağ el, sağı gösterir) y = 1 (sol el ileriyi gösterir) z = 5 (noktanın altında yukarı çıkan bir merdiven var). Bu verilere göre sağ elin gösterdiği yönde 3 mt, sol elin gösterdiği istikamette 1 mt. yürüyerek bir nokta bulacaksın ve ardından bir merdiven seni bekliyor ve 5 mt tırmanarak nihayet olacaksın. kendini son noktada bul.

Diğer tüm terimler, vektörler üzerinde çeşitli işlemler, yani pratik problemleri çözmek için gerekli olan yukarıdaki açıklamanın iyileştirmeleridir. Tipik vektör problemleri üzerinde durarak bu daha katı tanımları gözden geçirelim.

Fiziksel örnekler vektör nicelikleri, uzayda hareket eden bir maddesel noktanın yer değiştirmesi, bu noktanın hızı ve ivmesi ve buna etki eden kuvvet olabilir.

geometrik vektörşeklinde iki boyutlu ve üç boyutlu uzayda sunulan yönlü segment... Bu, başlangıç ​​ve bitiş arasında ayrım yapan bir segmenttir.

Eğer A vektörün başlangıcıdır ve B- sonu, daha sonra vektör bir sembol veya bir küçük harf ile gösterilir. Şekilde vektörün sonu bir okla gösterilmiştir (Şekil 1)

Uzunluk(veya modül) bir geometrik vektörün, onu oluşturan parçanın uzunluğudur.

iki vektör denir eşit , paralel transfer yoluyla hizalanabiliyorlarsa (yönler örtüşüyorsa), yani. paralellerse, aynı yöne bakın ve eşit uzunluklara sahipler.

Fizikte, genellikle kabul edilir bağlantılı vektörler uygulama noktası, uzunluk ve yön tarafından verilir. Vektörün uygulama noktası önemli değilse, uzayda herhangi bir noktaya uzunluk ve yön korunarak aktarılabilir. Bu durumda vektöre denir. Bedava... Sadece dikkate almayı kabul edeceğiz ücretsiz vektörler.

Geometrik vektörler üzerinde doğrusal işlemler

Bir vektörü bir sayı ile çarpma

vektörün çarpımı numaraya göre bir vektörden zamanla germe (at) veya sıkıştırma (at) ile elde edilen bir vektör olarak adlandırılır ve vektörün yönü, eğer korunur ve eğer ise tam tersine değişir. (İncir. 2)

Tanımdan, vektörler ve = her zaman bir veya paralel doğrular üzerinde yer alır. Böyle vektörlere denir doğrusal... (Bu vektörlerin paralel olduğunu da söyleyebilirsiniz, ancak vektör cebirinde "eşdoğrusal" demek adettendir.) Tersi de doğrudur: eğer vektörler ve eşdoğrusal iseler, o zaman bunlar bağıntı ile ilişkilidir.

Bu nedenle eşitlik (1) iki vektör için eşdoğrusallık koşulunu ifade eder.

Vektörlerin toplanması ve çıkarılması

Vektörleri eklerken şunu bilmeniz gerekir. toplam vektörler ve başlangıcı vektörün başlangıcına denk gelen ve sonu - vektörün başlangıcının vektörün sonuna eklenmesi şartıyla vektörün sonu ile çakışan bir vektör olarak adlandırılır. (Şekil 3)

Bu tanım herhangi bir sonlu sayıda vektöre dağıtılabilir. Yer verilsin nücretsiz vektörler. Birkaç vektör eklerken, kapanış vektörü, başlangıcı ilk vektörün başlangıcıyla ve bitiş - son vektörün sonuyla çakışan toplamları olarak alınır. Yani, vektörün başlangıcını vektörün sonuna, vektörün başlangıcını vektörün sonuna vb. eklerseniz. ve son olarak, vektörün sonuna - vektörün başlangıcına, sonra bu vektörlerin toplamı kapanış vektörüdür başlangıcı ilk vektörün başlangıcı ile çakışan ve sonu - son vektörün sonu ile. (Şek. 4)

Terimlere vektörün bileşenleri denir ve formüle edilen kural şudur: çokgen kuralı... Bu çokgen düz olmayabilir.

Bir vektörü -1 ile çarptığınızda zıt vektörü elde edersiniz. Vektörler ve aynı uzunluk ve zıt yönlere sahiptir. Onların toplamı verir sıfır vektör kimin uzunluğu sıfırdır. Sıfır vektörünün yönü tanımsızdır.

Vektör cebirinde, çıkarma işlemini ayrı ayrı ele almaya gerek yoktur: bir vektörden bir vektörü çıkarmak, vektöre zıt vektörü eklemek anlamına gelir, yani.

Örnek 1.İfadeyi basitleştirin:

.

,

yani vektörler polinomlarla aynı şekilde toplanabilir ve sayılarla çarpılabilir (özellikle ifadeleri basitleştirme görevleri). Genellikle, vektörlerin çarpımlarını hesaplamadan önce, vektörlerle doğrusal olarak benzer ifadeleri basitleştirme ihtiyacı ortaya çıkar.

Örnek 2. Vektörler ve ABCD paralelkenarının köşegenleri olarak işlev görür (Şekil 4a). Bu paralelkenarın kenarları olan ve her iki vektör cinsinden ifade edin.

Çözüm. Paralelkenar köşegenlerinin kesişme noktası her köşegeni ikiye böler. Problem ifadesinde gerekli olan vektörlerin uzunluklarını, ya istenilenlerle bir üçgen oluşturan vektörlerin toplamının yarısı, ya da farkların yarısı (köşegen olarak görev yapan vektörün yönüne bağlı olarak) olarak buluruz. ikinci durumda, eksi işaretiyle alınan toplamın yarısı. Sonuç, problem ifadesinde gerekli olan vektörlerdir:

Bu dersin başındaki Girişimcilik ve Yenilikçi Yetenek vektörleriyle ilgili soruyu artık doğru yanıtladığınıza inanmak için her türlü neden var. Doğru cevap: Bu vektörler üzerinde toplama işlemi yapılmaktadır.

Vektör problemlerini kendiniz çözün ve ardından çözümleri görün

Vektörlerin toplamının uzunluğu nasıl bulunur?

Bu görev, trigonometrik özelliklerin kullanımını içerdiğinden vektör işlemlerinde özel bir yer tutar. Diyelim ki aşağıdaki gibi bir görevle karşılaştınız:

Vektörlerin uzunlukları verildiğinde ve bu vektörlerin toplamının uzunluğu. Bu vektörler arasındaki farkın uzunluğunu bulun.

Bu ve diğerleri için çözümler benzer görevler ve bunların nasıl çözüleceğine dair bir açıklama - derste " Vektör toplama: vektör toplam uzunluk ve kosinüs teoremi ".

Ve bu tür sorunların çözümünü adresinden kontrol edebilirsiniz. Çevrimiçi hesap makinesi "Bir üçgenin bilinmeyen tarafı (vektör toplama ve kosinüs teoremi)" .

Vektörlerin ürünleri nerede?

Vektörden vektöre ürünler doğrusal işlemler değildir ve ayrı olarak değerlendirilir. Ve Vektörlerin ve Vektörlerin Nokta Çarpımı ve Vektörlerin Karışık Çarpımı öğreticilerimiz var.

Bir vektörün bir eksene yansıması

Vektörün eksene izdüşümü, vektör ile eksen arasındaki açının kosinüsü ile yansıtılan vektörün uzunluğunun ürününe eşittir:

Bildiğiniz gibi, noktanın izdüşümü A düz bir çizgide (düzlem), bu noktadan düz bir çizgiye (düzlem) bırakılan dikeyin tabanıdır.

İsteğe bağlı bir vektör olsun (Şekil 5) ve başlangıcının izdüşümleri olsun (noktalar A) ve bitiş (puan B) eksen başına ben... (Bir noktanın izdüşümünü oluşturmak için A) noktadan geçen düz bir çizgi üzerinde A düz çizgiye dik düzlem. Doğrunun ve düzlemin kesişimi, gerekli izdüşümünü tanımlayacaktır.

vektör bileşeni l ekseninde bu eksende yatan, başlangıcı başlangıcın izdüşümü ile çakışan ve sonu - vektörün sonunun izdüşümü ile çakışan bir vektör olarak adlandırılır.

Vektörün eksene izdüşümü ben numarayı aradı

,

bileşenlerin yönü eksen yönü ile çakışıyorsa, artı işareti ile alınan bu eksen üzerindeki bileşen vektörünün uzunluğuna eşittir ben, ve bu yönler zıt ise eksi işareti ile.

Eksen üzerindeki vektör izdüşümlerinin temel özellikleri:

1. Eşit vektörlerin aynı eksen üzerindeki izdüşümleri birbirine eşittir.

2. Bir vektörü bir sayı ile çarparken, izdüşümü aynı sayı ile çarpılır.

3. Vektörlerin toplamının herhangi bir eksen üzerindeki izdüşümü, aynı eksendeki vektörlerin toplamlarının izdüşümlerinin toplamına eşittir.

4. Vektörün eksene izdüşümü, vektör ile eksen arasındaki açının kosinüsü ile yansıtılan vektörün uzunluğunun ürününe eşittir:

.

Çözüm. Vektörleri bir eksene yansıt ben yukarıdaki teorik arka planda tanımlandığı gibi. Şekil 5a'dan, vektörlerin toplamının izdüşümü vektörlerin izdüşümlerinin toplamına eşit olduğu açıktır. Bu projeksiyonları hesaplıyoruz:

Vektörlerin toplamının son izdüşümünü bulun:

Bir vektörün uzayda dikdörtgen bir Kartezyen koordinat sistemi ile ilişkisi

ile tanışma ilgili derste uzayda dikdörtgen bir Kartezyen koordinat sistemi yer aldı, yeni bir pencerede açılması arzu edilir.

Sıralı bir koordinat sisteminde 0xyz eksen Öküz aranan apsis, eksen 0 yıl – y ekseni ve eksen 0z – eksen uygulaması.

keyfi bir nokta ile m vektör ilişkilendirdiğimiz uzay

aranan yarıçap vektörü puan m ve koordinat eksenlerinin her birine yansıtın. Karşılık gelen projeksiyonların değerlerini gösterelim:

sayılar x, y, z arandı M noktasının koordinatları, sırasıyla apsis, ordinat ve başvurmak, ve sıralı bir sayı noktası olarak yazılır: M (x; y; z)(şek. 6).

Yönü eksenin yönü ile çakışan birim uzunluktaki vektöre denir. birim vektör(veya ortom) eksen. ile belirtelim

Buna göre koordinat eksenlerinin birim vektörleri Öküz, Oy, Öz

Teorem. Herhangi bir vektör, koordinat eksenlerinin birim vektörleri boyunca genişletilebilir:

(2)

Eşitlik (2), vektörün koordinat eksenleri boyunca genişlemesi olarak adlandırılır. Bu genişlemenin katsayıları, vektörün koordinat eksenleri üzerindeki izdüşümleridir. Böylece vektörün koordinat eksenleri boyunca genişleme katsayıları (2) vektörün koordinatlarıdır.

Uzayda belirli bir koordinat sistemi seçildikten sonra, vektör ve koordinatlarının üçlüsü birbirini benzersiz olarak belirler, böylece vektör formda yazılabilir.

Vektörün (2) ve (3) biçimindeki temsilleri aynıdır.

Koordinatlardaki vektörler için eşdoğrusallık koşulu

Daha önce de belirttiğimiz gibi, vektörler bağıntı ile ilişkiliyse eşdoğrusal olarak adlandırılır.

vektörler olsun ... Bu vektörler, vektörlerin koordinatları bağıntı ile ilişkiliyse eşdoğrusaldır.

,

yani vektörlerin koordinatları orantılıdır.

Örnek 6. Verilen vektörler ... Bu vektörler doğrusal mı?

Çözüm. Bu vektörlerin koordinatlarının oranını bulalım:

.

Vektörlerin koordinatları orantılıdır, bu nedenle vektörler eşdoğrusaldır veya aynı olan paraleldir.

Vektör uzunluğu ve yön kosinüsleri

Koordinat eksenlerinin karşılıklı dikliği nedeniyle vektörün uzunluğu

vektörler üzerine inşa edilmiş dikdörtgen bir paralelyüzün köşegen uzunluğuna eşittir

ve eşitlik ile ifade edilir

(4)

Vektör tamamen iki nokta (başlangıç ​​ve bitiş) belirtilerek tanımlanır, böylece vektörün koordinatları bu noktaların koordinatları cinsinden ifade edilebilir.

Verilen bir koordinat sisteminde vektörün orijini şu noktada olsun:

ve son noktada

eşitlikten

Bunu takip eder

veya koordinat biçiminde

Buradan, vektörün koordinatları, aynı adı taşıyan vektörün sonu ve başlangıcının koordinatlarının farklılıklarına eşittir. ... Formül (4) bu durumda formu alır

Vektörün yönü ile belirlenir yön kosinüsleri ... Bunlar vektörün eksenlerle oluşturduğu açıların kosinüsleridir. Öküz, Oy ve Öz... Bu açıları sırasıyla gösterelim. α , β ve γ ... Daha sonra bu açıların kosinüsleri formüllerle bulunabilir.

Bir vektörün yönlü kosinüsleri de bu vektörün birim vektörünün koordinatlarıdır ve dolayısıyla vektör vektörü

.

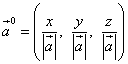
Vektörün uzunluğunun bir birime eşit olduğu göz önüne alındığında, yani

,

yön kosinüsleri için aşağıdaki eşitliği elde ederiz:

Örnek 7. Bir vektörün uzunluğunu bulun x = (3; 0; 4).

Çözüm. Vektörün uzunluğu

Örnek 8. Puan verilir:

Bu noktalar üzerine kurulan üçgenin ikizkenar olup olmadığını öğrenin.

Çözüm. Vektörün (6) uzunluğu formülünü kullanarak, kenarların uzunluklarını bulur ve aralarında iki eşit olup olmadığını belirleriz:

İki eşit kenar bulundu, bu nedenle üçüncü kenarın uzunluğunu aramaya gerek yok ve verilen üçgen ikizkenar.

Örnek 9. Bir vektörün uzunluğunu ve yönünün kosinüslerini bulun: .

Çözüm. Vektör koordinatları verilir:

.

Vektörün uzunluğu kare kök vektörün koordinatlarının karelerinin toplamından:

.

Yön kosinüslerini bulun:

Vektör problemini kendiniz çözün ve ardından çözümü görün

Koordinat formunda belirtilen vektörler üzerinde işlemler

İki vektör verilsin ve bunların izdüşümleriyle verilmiş olsun:

Bu vektörler üzerindeki eylemleri gösterelim.

Oluşturulma Tarihi: 2009-04-11 15:25:51
Son düzenleme: 2012-02-08 09:19:45

Uzun zamandır bu makaleyi yazmak istemiyordum - materyali nasıl sunacağımı düşünüyordum. Ayrıca resim çizmeniz gerekiyor. Ama görüyorsunuz, bugün yıldızlar başarıyla oluştu ve vektörlerle ilgili bir yazı olacak. Bununla birlikte, bu sadece kaba bir taslak. Gelecekte, bu makaleyi birkaç ayrı makaleye böleceğim - yeterince materyal var. Ayrıca makale yavaş yavaş gelişecek: Üzerinde değişiklikler yapacağım. bir oturuşta tüm yönleri ortaya koymak mümkün olmayacaktır.

Vektörler, skaler değerler kullanılarak tanımlanması zor olan nicelikleri tanımlamak için on dokuzuncu yüzyılda matematikle tanıştırıldı.

Vektörler, bilgisayar oyunlarının geliştirilmesinde yaygın olarak kullanılmaktadır. Sadece geleneksel olarak değil - güç veya hız gibi nicelikleri tanımlamak için değil, aynı zamanda vektörlerle hiçbir ilgisi olmayan alanlarda da kullanılırlar: renk depolamak, gölgeler oluşturmak.

Skaler ve vektörler

Öncelikle, size skalerin ne olduğunu ve bir vektörden nasıl farklı olduğunu hatırlatayım.

Skaler değerler bazı miktarları saklar: kütle, hacim. Yani, yalnızca bir sayı ile karakterize edilen bir varlıktır (örneğin, bir şeyin miktarı).

Bir vektör, skalerden farklı olarak iki değer kullanılarak tanımlanır: büyüklük ve yön.

Vektörler ve koordinatlar arasındaki önemli bir fark: vektörler belirli bir konuma bağlı değildir! Bir kez daha, bir vektördeki ana şey uzunluk ve yöndür.

Bir vektör, Latin alfabesinin kalın bir harfiyle gösterilir. Örneğin: a, B, v.

İlk şekilde, vektörün düzlemde nasıl tanımlandığını görebilirsiniz.

uzayda vektörler

Uzayda vektörler koordinatlar kullanılarak ifade edilebilir. Ama önce bir konsept tanıtmanız gerekiyor:

Nokta yarıçapı vektörü

Uzayda bir M (2,1) noktası alın. Bir noktanın yarıçap vektörü, orijinde başlayan ve noktada biten bir vektördür.

Burada bir vektörden başka bir şeyimiz yok OM... Vektör başlangıç ​​koordinatları (0,0), bitiş koordinatları (2,1). Bu vektörü şu şekilde gösteriyoruz: a.

Bu durumda vektör aşağıdaki gibi yazılabilir. a = <2, 1>... Bu vektörün koordinat formudur. a.

Bir vektörün koordinatlarına, eksenlere göre bileşenleri denir. Örneğin, 2 bir vektör bileşenidir a x ekseni hakkında.

Nokta koordinatlarının ne olduğuna bir kez daha bakalım. Bir noktanın koordinatı (örneğin, x), bir noktanın bir eksene izdüşümüdür, yani. dikin tabanı bir noktadan bir eksene düştü. Örneğimizde 2.

Ama ilk resme geri dönelim. Burada A ve B olmak üzere iki noktamız var. Noktaların koordinatları (1,1) ve (3,3) olsun. Vektör v bu durumda aşağıdaki gibi gösterilebilir v = <3-1, 3-1>... Üç boyutlu uzayda iki noktada bulunan bir vektör şöyle görünecektir:

v =

Bence burada zorluk yok.

Bir vektörü bir skaler ile çarpma

Bir vektör skaler değerlerle çarpılabilir:

k v = =

Bu, vektörün her bir bileşeniyle skaler değeri çarpar.

k> 1 ise vektör artacak, k birden küçük ama sıfırdan büyükse vektörün uzunluğu azalacaktır. k sıfırdan küçükse, vektör yön değiştirecektir.

Birim vektörler

Birim vektörler, uzunlukları bire eşit olan vektörlerdir. Koordinatlı vektöre dikkat edin<1,1,1>bire eşit olmayacak! Vektörün uzunluğunu bulma metinde aşağıda açıklanmıştır.

Sözde birim vektörler vardır - bunlar koordinat eksenleriyle aynı doğrultuda olan birim vektörlerdir. ben- x ekseninin birim vektörü, J- y ekseninin birim vektörü, k z ekseninin birim vektörüdür.

nerede ben = <1,0,0>, J = <0,1,0>, k = <0,0,1>.

Artık bir vektörün bir skaler ile çarpımının ne olduğunu ve birim vektörlerin ne olduğunu biliyoruz. şimdi yazabiliriz v vektör biçiminde.

v= vx ben+ v y J+ v z k, burada v x, v y, v z vektörün karşılık gelen bileşenleridir

Vektör ilavesi

Önceki formülü tam olarak anlamak için vektör toplamanın nasıl çalıştığını anlamanız gerekir.

Burada her şey basit. İki vektör alın v1 = ve v 2 =

v1 + v2 =

Sadece iki vektörün karşılık gelen bileşenlerini ekliyoruz.

Fark aynı şekilde hesaplanır.

Bu matematiksel formla ilgilidir. Tamlık için, vektörlerin toplama ve çıkarma işlemlerinin grafiksel olarak nasıl görüneceğini düşünmeye değer.

İki vektör eklemek için a+B... Vektörün başlangıcını eşleştirmeniz gerekir B ve vektörün sonu a... Ardından, vektörün başlangıcı arasında a ve vektörün sonu B yeni bir vektör çizin. Netlik için ikinci şekle bakın ("a" harfi).

Vektörleri çıkarmak için, iki vektörün başlangıcını birleştirmeniz ve ikinci vektörün sonundan birincinin sonuna kadar yeni bir vektör çizmeniz gerekir. İkinci resim ("b" harfi) nasıl göründüğünü gösterir.

Vektör uzunluğu ve yönü

Önce uzunluğa bakalım.

Uzunluk, vektörün yön hariç sayısal değeridir.

Uzunluk, formülle belirlenir (üç boyutlu bir vektör için):

vektör bileşenlerinin karelerinin toplamının karekökü.

Tanıdık bir formül, değil mi? Genel olarak, bu bir segmentin uzunluğu için formüldür.

Vektörün yönü, vektör ile koordinat eksenleri arasında oluşan açıların yön kosinüsleri ile belirlenir. Kosinüs yönünü bulmak için karşılık gelen bileşenler ve uzunluk kullanılır (resim daha sonra olacaktır).

Programlarda vektörleri temsil etme

Programlarda vektörleri temsil etmenin çeşitli yolları vardır. Hem verimli olmayan sıradan değişkenler yardımıyla hem de diziler, sınıflar ve yapılar yardımıyla.

Float vektörü3 = (1,2,3); // vektör depolamak için dizi struct vektör3 // vektörleri depolamak için yapı (float x, y, z;);

Vektörleri depolamak için en büyük olanaklar sınıflar tarafından sağlanır. Sınıflarda sadece vektörün kendisini (değişkenler) değil, aynı zamanda vektör işlemlerini (fonksiyonları) da tanımlayabiliriz.

Vektörlerin nokta çarpımı

İki tür vektör çarpması vardır: vektör ve skaler.

Nokta çarpımının ayırt edici bir özelliği, sonucun her zaman bir skaler değer olacağıdır, yani. sayı.

Burada şu noktaya dikkat etmekte fayda var. Bu işlemin sonucu sıfırsa, iki vektör diktir - aralarındaki açı 90 derecedir. Sonuç sıfırdan büyükse, açı 90 dereceden küçüktür. Sonuç sıfırdan küçükse, açı 90 dereceden büyüktür.

Bu işlem aşağıdaki formülle temsil edilir:

a · B= bir x * b x + bir y * b y + bir z * b z

Nokta ürün, iki vektörün karşılık gelen bileşenlerinin ürünlerinin toplamıdır. Onlar. İki vektörün x "s'sini alın, çarpın, sonra bunları y" s'nin çarpımı ile ekleyin, vb.

Vektörlerin vektör çarpımı

İki vektörün vektör çarpımı, bu vektörlere dik bir vektörle sonuçlanacaktır.

a x B =

Bu formülü henüz ayrıntılı olarak tartışmayacağız. Ayrıca, ezberlemesi oldukça zor. Belirleyicileri tanıdıktan sonra bu noktaya geri döneceğiz.

Genel gelişim için, elde edilen vektörün uzunluğunun, vektörler üzerine inşa edilen paralelkenarın alanına eşit olduğunu bilmek faydalıdır. a ve B.

vektör normalleştirme

Normalleştirilmiş bir vektör, uzunluğu bir olan bir vektördür.

Normalleştirilmiş vektörü bulma formülü aşağıdaki gibidir - vektörün tüm bileşenleri uzunluğuna bölünmelidir:

v n = v/ |v | =

son söz

Muhtemelen görmüş olduğunuz gibi, vektörleri anlamak zor değildir. Bir dizi vektör işlemini ele aldık.

"Matematik" bölümünün sonraki makalelerinde matrisleri, determinantları, sistemleri tartışacağız. lineer denklemler... Bunların hepsi teori.

Bundan sonra matris dönüşümlerine bakacağız. İşte o zaman bilgisayar oyunları yaratmada matematiğin ne kadar önemli olduğunu anlayacaksınız. Bu konu sadece önceki tüm konular için bir uygulama haline gelecektir.