Касательная плоскость. Теоретический материал Уравнение касательной плоскости

Скачать с Depositfiles

4. ТЕОРИЯ ПОВЕРХНОСТЕЙ.

4.1 УРАВНЕНИЯ ПОВЕРХНОСТЕЙ.

Поверхность в трёхмерном пространстве может быть задана:

1) неявно: F ( x , y , z ) =0 (4.1)

2) явно: z = f ( x , y ) (4.2)

3) параметрически: (4.3)

или:
(4.3’)

где скалярные аргументы
иногда называют криволинейными координатами. Например, сферу
удобно задавать в сферических координатах:
.

4.2 КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ.

Если линия лежит на поверхности (4.1), то координаты её точек удовлетворяют уравнению поверхности:

Дифференцируя это тождество, получим:

(4.4)

или
(4.4 ’ )

в каждой точке кривой на поверхности. Таким образом, вектор градиента в неособых точках поверхности (в которых функция (4.5) дифференцируема и
) перпендикулярен касательным векторам к любым линиям на поверхности, т.е может быть использован в качестве вектора нормали для составления уравнения касательной плоскости в точке М 0 (x 0 , y 0 , z 0 ) поверхности

(4.6)

и в качестве направляющего вектора в уравнении нормали:

(4.7)

В случае явного (4.2) задания поверхности уравнения касательной плоскости и нормали соответственно примут вид:

(4.8)

и
(4.9)

При параметрическом представлении поверхности (4.3) векторы
лежат в касательной плоскости и уравнение касательной плоскости может быть записано в виде:

(4.10)

а в качестве направляющего вектора нормали может быть принято их векторное произведение:

и уравнение нормали может быть записано в виде:

(4.11)

где
— значения параметров соответствующие точке М 0 .

В дальнейшем мы ограничимся рассмотрением лишь таких точек поверхности, где векторы

не равны нулю и не параллельны.

Пример 4.1 Составить уравнения касательной плоскости и нормали в точке М 0 (1,1,2) к поверхности параболоида вращения
.

Решение: Так как уравнение параболоида задано в явном виде, то согласно (4.8) и (4.9) нужно найти
в точке М 0 :

, а в точке М 0
. Тогда уравнение касательной плоскости в точке М 0 примет вид:

2(x -1)+2(y -1)-(z -2)=0 или 2 x +2 y – z ‑ 2=0, а уравнение нормали
.

Пример 4.2 Составить уравнения касательной плоскости и нормали в произвольной точке геликоида
, .

Решение. Здесь ,

Уравнение касательной плоскости:

или

Уравнения нормали:

.

4.3 ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.

Если поверхность задается уравнением

то кривая
на ней может быть задана уравнением
(4.12)

Дифференциал радиус-вектора
вдоль кривой, отвечающий смещению из точки М 0 в близлежащую точку М, равен

(4.13)

Так как
— дифференциал дуги кривой, отвечающий тому же смещению), то

(4.14)

где .

Выражение в правой части (4.14) называется первой квадратичной формой поверхности и играет в теории поверхностей огромную роль.

Интегрирую дифференциал ds в пределах от t 0 (соответствует точке М 0 ) до t (соответствует точке М), получим длину соответствующего отрезка кривой

(4.15)

Зная первую квадратичную форму поверхности, можно находить не только длины, но и углы между кривыми.

Если du , dv — дифференциалы криволинейных координат, отвечающие бесконечно малому смещению по одной кривой, а
— по другой, то с учетом (4.13):

(4.16)

С помощью формулы

(4.17)

первая квадратичная форма дает возможность вычислить площадь области
поверхности.

Пример 4.3 На геликоиде , найти длину винтовой линии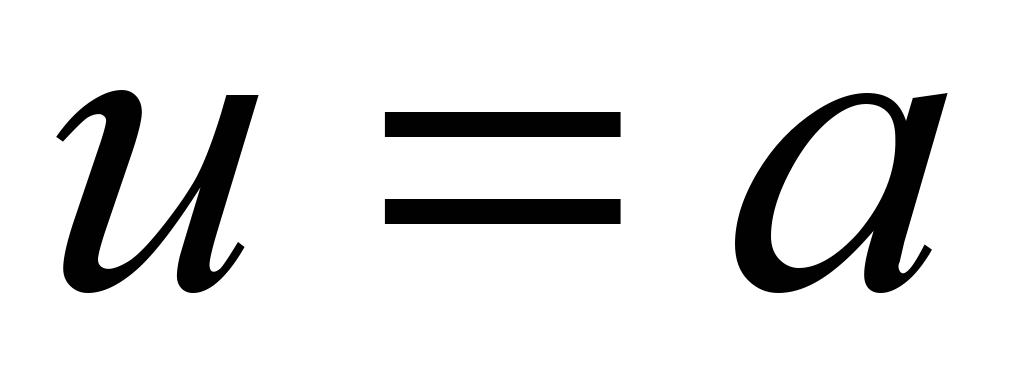
между двумя точками .

Решение. Поскольку на винтовой линии
, то . Найдём в точке
первую квадратичную форму. Обозначив и v = t , получим уравнение данной винтовой линии в виде . Квадратичная форма:

= ‑ первая квадратичная форма.

Здесь . В формуле (4.15) в данном случае
и длина дуги:

=

4.4 ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.

Обозначим
‑ единичный вектор нормали к поверхности
:

(4.18) . (4.23)

Линия на поверхности называется линией кривизны, если ее направление в каждой точке является главным направлением.

4.6 ПОНЯТИЕ О ГЕОДЕЗИЧЕСКИХ ЛИНИЯХ НА ПОВЕРХНОСТИ.

Определение 4.1 . Кривая на поверхности называется геодезической, если ее главная нормаль в каждой точке, где кривизна отлична от нуля, совпадает с нормалью к поверхности.

Через каждую точку поверхности в любом направлении проходит, и при том только одна геодезическая. На сфере, например, геодезическими являются большие круги.

Параметризация поверхности называется полугеодезической, если одно семейство координатных линий состоит из геодезических, а второе ему ортогонально. Например, на сфере меридианы (геодезические) и параллели.

Геодезическая на достаточно малом отрезке является кратчайшей среди всех близких к ней кривых, соединяющих те же точки.

Уравнение нормальной плоскости

1.

4.

Касательная плоскость и нормаль к поверхности

Пусть дана некоторая поверхность, A — фиксированная точка поверхности и B — переменная точка поверхности,

(рис. 1).

Ненулевой вектор

→

n

называется нормальным вектором к поверхности в точке A , если

lim B → A j = π 2 .

Точка поверхности F (x , y , z) = 0 называется обыкновенной , если в этой точке

1. частные производные F " x , F " y , F " z непрерывны;
2. (F " x )2 + (F " y )2 + (F " z )2 ≠ 0 .

При нарушении хотя бы одного из этих условий точка поверхности называется особой точкой поверхности .

Теорема 1. Если M (x 0 , y 0 , z 0 ) — обыкновенная точка поверхности F (x , y , z) = 0 , то вектор

→ n = grad F (x 0 , y 0 , z 0 ) = F " x (x 0 , y 0 , z 0 ) → i + F " y (x 0 , y 0 , z 0 ) → j + F " z (x 0 , y 0 , z 0 ) → k

(1)

является нормальным к этой поверхности в точке M (x 0 , y 0 , z 0 ) .

Доказательство приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова ``Курс высшей математики: Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения. М.: Изд-во МЭИ, 2002 (стр. 128).

Нормалью к поверхности в некоторой ее точке называется прямая, направляющий вектор которой является нормальным к поверхности в этой точке и которая проходит через эту точку.

Канонические уравнения нормали можно представить в виде

x − x 0 F " x (x 0 , y 0 , z 0 ) = y − y 0 F " y (x 0 , y 0 , z 0 ) = z − z 0 F " z (x 0 , y 0 , z 0 ) .

(2)

Касательной плоскостью к поверхности в некоторой точке называется плоскость, которая проходит через эту точку перпендикулярно нормали к поверхности в этой точке.

Из этого определения следует, что уравнение касательной плоскости имеет вид:

(3)

Если точка поверхности является особой, то в этой точке нормальный к поверхности вектор может не существовать, и, следовательно, поверхность может не иметь нормали и касательной плоскости.

Геометрический смысл полного дифференциала функции двух переменных

Пусть функция z = f (x , y) дифференцируема в точке a (x 0 , y 0 ) . Ее графиком является поверхность

f (x , y) − z = 0.

Положим z 0 = f (x 0 , y 0 ) . Тогда точка A (x 0 , y 0 , z 0 ) принадлежит поверхности.

Частные производные функции F (x , y , z) = f (x , y) − z суть

F " x = f " x , F " y = f " y , F " z = − 1

и в точке A (x 0 , y 0 , z 0 )

1. они непрерывны;
2. F "2 x + F "2 y + F "2 z = f "2 x + f "2 y + 1 ≠ 0 .

Следовательно, A — обыкновенная точка поверхности F (x , y , z) и в этой точке существует касательная плоскость к поверхности. Согласно (3), уравнение касательной плоскости имеет вид:

f " x (x 0 , y 0 ) (x − x 0 ) + f " y (x 0 , y 0 ) (y − y 0 ) − (z − z 0 ) = 0.

Вертикальное смещение точки на касательной плоскости при переходе из точки a (x 0 , y 0 ) в произвольную точку p (x , y) есть B Q (рис. 2). Соответствующее приращение аппликаты есть

(z − z 0 ) = f " x (x 0 , y 0 ) (x − x 0 ) + f " y (x 0 , y 0 ) (y − y 0 )

Здесь в правой части стоит дифференциалd z функции z = f (x , y) в точке a (x 0 , x 0 ). Следовательно,
d f (x 0 , y 0 ). есть приращение аппликаты точки плоскости касательной к графику функции f (x , y) в точке (x 0 , y 0 , z 0 = f (x 0 , y 0 )).

Из определения дифференциала следует, что расстояние между точкой P на графике функции и точкой Q на касательной плоскости есть бесконечно малая более высокого порядка, чем расстояние от точки p до точки a .

Определение. Точка , лежащая на поверхности второго порядка, заданной относительно ОДСК общим уравнением (1) называется неособой, если среди трёх чисел: есть хотя бы одно, не равное нулю.

Таким образом, точка , лежащая на поверхности второго порядка, является не особой тогда и только тогда, когда она является её центром, иначе, когда поверхность коническая, а точка - вершина этой поверхности.

Определение. Касательной прямой к поверхности второго порядка в данной на ней не особой точке называется прямая, проходящая через эту точку, пересекающая поверхность второго порядка в дву-кратной точке или являющаяся прямолинейной образующей поверхности.

Теорема 3. Касательные прямые к поверхности второго порядка в данной на ней не особой точке лежат в одной плоскости, называемой касательной плоскостью к поверхности в рассматриваемой точке. Уравнение касательной плоскости имеет

Доказательство. Пусть , , параметрические уравнения прямой, проходящей через неособую точку по-верхности второго порядка, заданной уравнением (1). Подставляя в уравнение (1) , , вместо , , , получим:

Так как точка лежит на поверхности (1), то и из уравнения (3) находим (это значение соответствует точке ). Для того, чтобы точка пересечения прямой с поверхностью (1) была двойной, или чтобы прямая целиком лежала на поверхности, необходимо и достаточно, чтобы выполнялось равенство:

Если при этом:

То точка пересечения прямой линии с поверхностью (1) двойная. А если:

То прямая целиком лежит на поверхности (1).

Из соотношений (4) и , , следует, что координаты , , любой точки , лежащей на любой касательной к поверхности (1) удовлетворяют уравнению:

Обратно, если координаты какой-нибудь точки , отличной от , удовлетворяют этому уравнению, то координаты , , вектора , удовлетворяют соотношению (4), а это значит, что прямая - касательная к рассматриваемой поверхности.

Так как точка - неособая точка поверхности (1), то среди чисел , , есть по крайней мере одно, не равное нулю; значит уравнение (5) есть уравнение первой степени относительно . Это и есть уравнение плоскости, касательной к поверхности (1) в данной на ней не особой точке .

Исходя из канонических уравнений поверхностей второго порядка легко составить уравнения касательных плоскостей к эллипсоиду, гиперболоиду и т.д. в данной на них точке .

1). Касательная плоскость к эллипсоиду:

2). Касательная плоскость к одно и двуполостному гиперболоидам:

3). Касательная плоскость к эллиптическому и гиперболическому параболоидам:

§ 161.Пересечение касательной плоскости с поверхностью второго порядка.

Примем неособую точку поверхности второго порядка за начало координат ОДСК, оси и расположим в плоскости касательной к поверхности в точке . Тогда в общем уравнении поверхности (1) свободный член равен нулю: , а уравнение плос-кости, касающейся поверхности в начале координат, должно иметь вид: .

Но уравнение плоскости, проходящей через начало координат имеет вид: .

И, так как это уравнение должно быть эквивалентно уравнению , то , , .

Итак, в выбранной системе координат уравнение поверхности (1) должно иметь вид:

Обратно, если , то уравнение (6) является уравнением поверхности, проходящей через начало координат , а плоскость - касательная плоскость к этой поверхности в точке . Уравнение линии, по которой касательная плоскость к поверхности в точке пересекает поверхность (6) имеет вид:

Если . Это инвариант в теории инвариантов для линий второго порядка. Уравнение (7)

Это же линия второго порядка. По виду этой линии инвариант , поэтому:

При здесь две мнимые пересекающиеся прямые.

При - две действительные пересекающиеся прямые.

Если , но хотя бы один из коэффициентов , , не равен нулю, то линия пересечения (7) - две совпадающие прямые.

Наконец, если , то плоскость

входит в состав данной поверхности, а сама поверхность распадается, следовательно, на пару плоскостей

§ 162.Эллиптические, гиперболические или параболические точки поверхности второго порядка.

1. Пусть касательная плоскость к поверхности второго порядка в точке пересекает её по двум мни-мым пересекающимся прямым. В этом случае точка называется эллиптической точкой поверхности.

2. Пусть касательная плоскость к поверхности второго порядка в точке пересекает её по двум действительным прямым, пересекающимся в точке касания. В этом случае точка называется гиперболической точкой поверхности.

3. Пусть касательная плоскость к поверхности второго порядка в точке пересекает её по двум совпадающим прямым. В этом случае точка называется параболической точкой поверхности.

Теорема 4. Пусть поверхность второго порядка относительно ОДСК задана уравнением (1) и данное уравнение (1) является уравнением действительной нераспадающейся поверхностью второго порядка. Тогда, если ; то все точки поверхности эллиптические.

Доказательство. Введём новую систему координат , выбирая за начало координат любую неособую точку данной поверхности и располагая оси и в плоскости, касательной к поверхности в точке . Уравнение (1) в новой системе координат преобразуется к виду:

Где . Вычислим инвариант для этого уравнения .

Так как при переходе от одной ОДСК к другой ОДСК знак не меняется, то знаки и противоположны, поэтому, если , то ; и, как следует из классификации (см. § 161) касательная плоскость к поверхности в точке пересекает поверхность по двум мнимым пересекающимся прямым, т.е. - эллиптическая точка.

2) Однополостный гиперболоид и гиперболический параболоид состоят из гиперболических точек.

3) Действительный конус второго порядка (вершина исключается), эллиптический (действительный), гиперболический и параболический цилиндры состоят из параболических точек.

Параболический цилиндр .

Чтобы определить расположение параболического цилиндра, достаточно знать:

1) плоскость симметрии, параллельную образующим цилиндра;

2) касательную плоскость к цилиндру, перпендикулярную к этой плоскости симметрии;

3) вектор, перпендикулярный к этой касательной плоскости и направленный в сторону вогнутости цилиндра.

В случае, если общее уравнение определяет параболический цилиндр, оно может быть переписано в виде:

Подберем m так, чтобы плоскости

были бы взаимно перпендикулярными:

При этом значении m плоскость

будет плоскостью симметрии, параллельной образующим цилиндра.

Плоскость

будет касательной плоскостью к цилиндру, перпендикулярной к указанной плоскости симметрии, а вектор

будет перпендикулярен к найденной касательной плоскости и направлен в сторону вогнутости цилиндра.

Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.
Рассмотрим поверхность σ , заданную уравнением z = f(x,y) , где f(x,y) – дифференцируемая функция, и пусть M 0 (x 0 ,y 0 ,z 0) – фиксированная точка на поверхности σ , т.е. z 0 = f(x 0 ,y 0). Назначение . Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности . Решение оформляется в формате Word . Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис .

Правила ввода функций :

Правила ввода функций :

1. Все переменные выражаются через x,y,z

Касательной плоскостью к поверхности σ в её точке М 0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М 0 .
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0) имеет вид:

z – z 0 = f’ x (x 0 ,y 0)(x – x 0) + f’ y (x 0 ,y 0)(y – y 0)

Вектор называется вектором нормали к поверхности σ в точке М 0 . Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М 0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0), где z 0 = f(x 0 ,y 0), имеют вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M 0 (0;1).
Решение . Запишем уравнения касательной в общем виде: z - z 0 = f" x (x 0 ,y 0 ,z 0)(x - x 0) + f" y (x 0 ,y 0 ,z 0)(y - y 0)
По условию задачи x 0 = 0 , y 0 = 1 , тогда z 0 = 5
Найдем частные производные функции z = x^3+5*y:
f" x (x,y) = (x 3 +5 y)" x = 3 x 2
f" x (x,y) = (x 3 +5 y)" y = 5
В точке М 0 (0,1) значения частных производных:
f" x (0;1) = 0
f" y (0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z - 5 = 0(x - 0) + 5(y - 1) или -5 y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M 0 (1;0;1).
Решение . Находим частные производные функции . Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М 0 (1,0,1) значения частных производных:
f" x (1;0;1) = -3 / 16
f" y (1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z - 1 = -3 / 16 (x - 1) + 0(y - 0) или 3 / 16 x+z- 19 / 16 = 0

Пример . Поверхность σ задана уравнением z = y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М 0 (x 0 , y 0 , z 0), принадлежащей ей, если x 0 = –1, y 0 = 2.
Найдем частные производные функции z = f (x , y ) = y/x + xy – 5x 3:
f x ’(x , y ) = (y/x + xy – 5x 3)’ x = – y/x 2 + y – 15x 2 ;
f y ’ (x , y ) = (y/x + xy – 5x 3)’ y = 1/x + x .
Точка М 0 (x 0 , y 0 , z 0) принадлежит поверхности σ , поэтому можно вычислить z 0 , подставив заданные x 0 = –1 и y 0 = 2 в уравнение поверхности:

z = y/x + xy – 5x 3

z 0 = 2/(-1) + (–1) 2 – 5 (–1) 3 = 1.
В точке М 0 (–1, 2, 1) значения частных производных:
f x ’(М 0) = –1/(-1) 2 + 2 – 15(–1) 2 = –15; f y ’(М 0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М 0:
z – 1= –15(x + 1) – 2(y – 2) z – 1= –15x – 15 – 2y + 4 15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М 0: .
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали: .

Пример №1 . Дана функция z=f(x,y) и две точки А(х 0 , y 0) и В(х 1 ,y 1). Требуется: 1) вычислить значение z 1 функции в точке В; 2) вычислить приближенное значение z 1 функции в точке В исходя из значения z 0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x 0 ,y 0 ,z 0).
Решение.
Запишем уравнения касательной в общем виде:
z - z 0 = f" x (x 0 ,y 0 ,z 0)(x - x 0) + f" y (x 0 ,y 0 ,z 0)(y - y 0)
По условию задачи x 0 = 1, y 0 = 2, тогда z 0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f" x (x,y) = (x 2 +3 x y +y 2)" x = 2 x+3 y 3
f" x (x,y) = (x 2 +3 x y +y 2)" y = 9 x y 2
В точке М 0 (1,2) значения частных производных:
f" x (1;2) = 26
f" y (1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0:
z - 25 = 26(x - 1) + 36(y - 2)
или
-26 x-36 y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).

Касательные плоскости играют большую роль в геометрии. Построение касательных плоскостей в практическом отношении имеет важное значение, так как наличие их позволяет определить направление нормали к поверхности в точке касания. Эта задача находит широкое применение в инженерной практике. К помощи касательных плоскостей обращаются также для построения очерков геометрических фигур, ограниченных замкнутыми поверхностями. В теоретическом плане плоскости, касательные к поверхности, используются в дифференциальной геометрии при изучении свойств поверхности в районе точки касания.

Основные понятия и определения

Плоскость, касательную к поверхности, следует рассматривать как предельное положение секущей плоскости (по аналогии с прямой, касательной к кривой, которая также определяется как предельное положение секущей).

Плоскость, касательная к поверхности в заданной на поверхности точке, есть множество всех прямых - касательных, проведенных к поверхности через заданную точку.

В дифференциальной геометрии доказывается, что псе касательные к поверхности, проведенные в обыкновенной точке, компланарны (принадлежат одной плоскости).

Выясним, как проводится прямая, касательная к поверхности. Касательная t к поверхности β в заданной на поверхности точке М (рис. 203) представляет предельное положение секущей l j , пересекающей поверхность в двух точках (ММ 1 , ММ 2 , ..., ММ n), когда точки пересечения совпадают (М ≡ М n , l n ≡ l M). Очевидно {M 1 , М 2 , ..., М n } ∈ g, так как g ⊂ β. Из сказанного выше вытекает следующее определение: касательной к поверхности называется прямая, касательная к какой-либо кривой, принадлежащей поверхности .

Так как плоскость определяется двумя пересекающимися прямыми, то для задания плоскости, касательной к поверхности в заданной точке, достаточно провести через эту точку две произвольные линии, принадлежащие поверхности (желательно простые по форме), и к каждой из них построить касательные в точке пересечения этих линий. Построенные касательные однозначно определяют касательную плоскость. Наглядное представление о проведении плоскости α, касательной к поверхности β в заданной точке М, дает рис. 204. На этом рисунке показана также нормаль n к поверхности β.

Нормлью к поверхности в заданной точке называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

Линию пересечении поверхности плоскостью, проходящей через нормаль, называют нормальным сечением поверхности. В зависимости от вида поверхности касательная плоскость может иметь, с поверхностью как одну, так и множество точек (линию). Линия касания может быть в то же время и линией пересечения поверхности с плоскостью.

Возможны также случаи, когда на поверхности имеются точки, на которых невозможно провести касательную к поверхности; такие точки называют особыми. В качестве примера особых точек можно привести точки, принадлежащие ребру возврата торсовой поверхности, или точку пересечения меридиана поверхности вращения с ее осью, если меридиан и ось пересекаются не под прямым углом.

Виды касания зависят от характера кривизны поверхности.

Кривизна поверхности

Вопросы кривизны поверхности были исследованы французским математиком Ф. Дюпеном (1784- 1873), который предложил наглядный способ изображения изменения кривизны нормальных сечений поверхности.

Для этого в плоскости, касательной к рассматриваемой поверхности в точке М (рис. 205, 206), на касательных к нормальным сечениям по обе стороны от данной точки откладываются отрезки, равные корням квадратным из величин соответствующих радиусов кривизны этих сечений. Множество точек - концов отрезков задают кривую, называемую индикатрисой Дюпена . Алгоритм построения индикатрисы Дюпена (рис. 205) можно записать:

1. M ∈ α, M ∈ β ∧ α β;

2. = √(R l 1), = √(R l 2),..., = √(R l n)

где R - радиус кривизны.

(A 1 ∪ А 2 ∪ ... ∪ А n) - индикатриса Дюпена.

Если индикатриса Дюпена поверхности - эллипс, то точка М называется эллиптической, а поверхность - поверхностью с эллиптическими точками (рис. 206). В этом случае касательная плоскость имеет с поверхностью только одну общую точку, а все линии, принадлежащие поверхности и пересекающиеся в рассматриваемой точке, расположены по одну сторону от касательной плоскости. Примером поверхностей с эллиптическими точками могут служить: параболоид вращения, эллипсоид вращения, сфера (в этом случае индикатриса Дюпена - окружность и др.).

При проведении касательной плоскости к торсовой поверхности плоскость будет касаться этой поверхности по прямой образующей. Точки этой прямой называются параболическими, а поверхность - поверхностью с параболическими точками . Индикатриса Дюпена в этом случае - две параллельные прямые (рис. 207*).

На рис. 208 показана поверхность, состоящая из точек, в кото

* Кривая второго порядка - парабола - при определенных условиях может распадаться на две действительные параллельные прямые, две мнимые параллельные прямые, две совпадающие прямые. На рис. 207 мы имеем дело с двумя действительными параллельными прямыми.

рых касательная плоскость пересекает поверхность. Такая поверхность называется гиперболической , а принадлежащие ей точки - гиперболическими точками. Индикатриса Дюпена в данном случае - гипербола.

Поверхность, все точки которой являются гиперболическими, имеет форму седла (косая плоскость, однополостный гиперболоид, вогнутые поверхности вращения и др.).

Одна поверхность может иметь точки разных видов, например, у торсовой поверхности (рис. 209) точка М эллиптическая; точка N - параболическая; точка К - гиперболическая.

В курсе дифференциальной геометрии доказывается, что нормальные сечения, в которых величины кривизны K j = 1/ R j (где R j радиус кривизны рассматриваемого сечения) имеют экстремальные значения, расположены в двух взаимно перпендикулярных плоскостях.

Такие кривизны К 1 = 1/R max . К 2 = 1/R min называются главными, а значения Н = (К 1 + К 2)/2 и К = К 1 К 2 - соответственно средней кривизной поверхности и полной (гауссовой) кривизной поверхности в рассматриваемой точке. Для эллиптических точек К > 0, гиперболических К

Задание плоскости касательной к поверхности на эпюре Монжа

Ниже на конкретных примерах покажем построение плоскости, касательной к поверхности с эллиптическими (пример 1), параболическими (пример 2) и гиперболическими (пример 3) точками.

ПРИМЕР 1. Построить плоскость α, касательную к поверхности вращения β, с эллиптическими точками. Рассмотрим два варианта решения этой задачи, а) точка М ∈ β и б) точка М ∉ β

Вариант а (рис. 210).

Касательная плоскость определяется двумя касательными t 1 и t 2 , проведенными в точке М к параллели и меридиану поверхности β.

Проекции касательной t 1 к параллели h поверхности β будут t" 1 ⊥ (S"M") и t" 1 || оси х. Горизонтальная проекция касательной t" 2 к меридиану d поверхности β, проходящему через точку М, совпадет с горизонтальной проекцией меридиана. Чтобы найти фронтальную проекцию касательной t" 2 , меридиональную плоскость γ(γ ∋ М) путем вращения вокруг оси поверхности β переводим в положение γ 1 , параллельное плоскости π 2 . В этом случае точка М → M 1 (М" 1 , М" 1).Проекция касательной t" 2 rarr; t" 2 1 определяется (M" 1 S"). Если мы теперь возвратим плоскость γ 1 в первоначальное положение, то точка S" останется на месте (как принадлежащая оси вращения), а М" 1 → М" и фронтальная проекция касательной t" 2 определится (M"S")

Две пересекающиеся в точке М ∈ β касательные t 1 и t 2 определяют плоскость α, касательную к поверхности β.

Вариант б (рис. 211)

Для построения плоскости, касательной к поверхности проходящей через точку, не принадлежащую поверхности, нужно исходить из следующих соображений: через точку вне поверхности, состоящей из эллиптических точек, можно провести множество плоскостей, касательных к поверхности. Огибающей этих поверхностей будет некоторая коническая поверхность. Поэтому, если нет дополнительных указаний, то задача имеет множество решений и в таком случае сводится к проведению конической поверхности γ, касательной к данной поверхности β.

На рис. 211 показано построение конической поверхности γ, касательной к сфере β. Любая плоскость α, касательная к конической поверхности γ, будет касательной к поверхности β.

Для построения проекций поверхности γ из точек М" и М" проводим касательные к окружностям h" и f" - проекциям сферы. Отмечаем точки касания 1 (1" и 1"), 2 (2" и 2"), 3 (3" и 3") и 4 (4" и 4"). Горизонтальная проекция окружности - линия касания конической поверхности и сферы спроецируется в [ 1"2"] Для нахождения точек эллипса, в который эта окружность спроецируется на фронтальную плоскость проекций, воспользуемся параллелями сферы.

На рис. 211 таким способом определены фронтальные проекции точек Е и F (Е" и F"). Имея коническую поверхность γ, строим к ней касательную плоскость α. Характер и последовательность графичес-

ких построений, которые необходимо для этого выполнить, приведены в следующем примере.

ПРИМЕР 2 Построить плоскость α, касательную к поверхности β с параболическими точками

Как в примере 1 рассмотрим два варианта решения.а) точка N ∈ β; б) точка N ∉ β

Вариант а (рис 212) .

Коническая поверхность относится к поверхностям с параболическими точками (см. рис. 207.) Плоскость, касательная к конической поверхности, касается ее по прямолинейной образующёи.Для ее построения необходимо:

1) через данную точку N провести образующую SN (S"N" и S"N") ;

2) отметить точку пересечения образующей (SN) с направляющей d: (SN) ∩ d = А;

3) провеет и к асательную t к d в точке А.

Образующая (SA) и пересекающая ее касательная t определяютплоскостъ α , касательную к конической поверхности β в данной точке N*.

Для проведения плоскости α, касательной к конической поверхности β и проходящей через точку N, не принадле

* Так как поверхность β состоит из параболических точек (кроме вершины S), то касательная к ней плоскость α будет иметь общую с ней не одну точку N, а прямую (SN).

жащую заданной поверхности, необходимо:

1) через данную точку N и вершину S конической поверхности β провести прямую а (а" и а") ;

2) определить горизонтальный след этой прямой Н a ;

3) через Н a провести касательные t" 1 и t" 2 кривой h 0β - горизонтальному следу конической поверхности;

4) точки касания А (А" и А") и В (В" и В") соединить с вершиной конической поверхности S (S" и S").

Пересекающиеся прямые t 1 , (AS) и t 2 , (BS) определяют искомые касательные плоскости α 1 и α 2

ПРИМЕР 3. Построить плоскость α, касательную к поверхности β с гиперболическими точками.

Точка К (рис. 214) находится на поверхности глобоида (внутренняя поверхность кольца).

Для определения положения касательной плоскости α необходимо:

1) провести через точку К параллель поверхности β h(h", h") ;

2) через точку К" провести касательную t" 1 (t" 1 ≡ h") ;

3) для определения направлений проекций касательной к меридиональному сечению необходимо провести через точку К и ось поверхности плоскость γ, горизонтальная проекция t" 2 совпадет с h 0γ ; для построения фронтальной проекции касательной t" 2 предварительно переведем плоскость γ путем вращения ее вокруг оси поверхности вращения в положение γ 1 || π 2 . В этом случае меридиональное сечение плоскостью γ совместится с левой очерковой дугой фронтальной проекции - полуокружностью g".

Точка К (К", К"), принадлежащая кривой меридионального сечения, переместится в положение K 1 (К" 1 , К" 1). Через К" 1 проводим фронтальную проекцию касательной t" 2 1 , в совмещенном с плоскостью γ 1 || π 2 положении и отмечаем точку ее пересечения с фронтальной проекцией оси вращения S" 1 . Возвращаем плоскость γ 1 в исходное положение, точка К" 1 → К" (точка S" 1 ≡ S"). Фронтальная проекция касательной t" 2 определится точками К" и S".

Касательные t 1 и t 2 определяют искомую касательную плоскость α, которая пересекает поверхность β по кривой l .

ПРИМЕР 4. Построить плоскость α, касательную к поверхности β в точке К. Точка К находится на поверхности однополостного гиперболоида вращения (рис. 215).

Эту задачу можно решить, придерживаясь алгоритма, использованного в предыдущем примере, но учитывая, что поверхность однополостного гиперболоида вращения является линейчатой поверхностью, которая имеет два семейства прямолинейных образующих, причем каждая из образующих одного семейства пересекает все образующие другого семейства (см. § 32, рис. 138). Через каждую точку этой поверхности можно провести две пересекающиеся прямые - образующие, которые будут одновременно касательными к поверхности однополостного гиперболоида вращения.

Эти касательные определяют касательную плоскость, т е. плоскость, касательная к поверхности однополостного гиперболоида вращения,пересекает эту поверхность по двум прямым g 1 и g 2 . Для построения проекций этих прямых достаточно ит горизонтальной проекции точки К пронести касательные t" 1 и t" 2 к горизон-

тальной проекции окружности d" 2 - горла поверхности однополостного гиперболоида вращения; определить точки 1" и 2 , в которых t" 1 и t" 2 пересекают одну ит направляющих поверхности d 1 . По 1" и 2" находим 1" и 2" , которые совместно с К" определяют фронтальные проекции искомых прямых.