Vektor. Asosiy xususiyatlar

Ta'rif Tartiblangan to'plam (x 1, x 2, ..., x n) n ta haqiqiy son deyiladi n o'lchovli vektor, va x i (i = 1, ..., n) raqamlari komponentlar yoki koordinatalar,

Misol. Agar, masalan, ma’lum bir avtomobil zavodi smenada 50 ta yengil avtomobil, 100 ta yuk avtomobili, 10 ta avtobus, yengil avtomobillar uchun 50 komplekt ehtiyot qismlar, yuk mashinalari va avtobuslar uchun 150 komplekt ishlab chiqarishi kerak bo‘lsa, ushbu zavodning ishlab chiqarish dasturini quyidagi shaklda yozish mumkin. besh komponentli vektor (50, 100, 10, 50, 150) shakli.

Belgilash. Vektorlar qalin kichik harflar yoki tepada chiziq yoki o'q bo'lgan harflar bilan belgilanadi, masalan, a yoki . Ikki vektor deyiladi teng agar ular bir xil miqdordagi komponentlarga ega bo'lsa va ularga mos keladigan komponentlar teng bo'lsa.

Vektor komponentlarini almashtirib bo'lmaydi, masalan, (3, 2, 5, 0, 1) va (2, 3, 5, 0, 1) turli vektorlardir.
Vektorlar ustida amallar. Mahsulot bo'yichax= (x 1, x 2, ..., x n) l haqiqiy songa l vektor deyiladi. x= (l x 1, l x 2, ..., l x n).

summasix= (x 1, x 2, ..., x n) va y= (y 1, y 2, ..., y n) vektor deyiladi x + y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

Vektorlar fazosi. N-o'lchovli vektor fazosi R n haqiqiy sonlarga ko'paytirish va qo'shish amallari aniqlangan barcha n o'lchovli vektorlar to'plami sifatida aniqlanadi.

Iqtisodiy illyustratsiya. n o'lchovli vektor fazosining iqtisodiy tasviri: tovarlar maydoni (tovarlar). ostida tovar biz ma'lum bir joyda ma'lum bir vaqtda sotuvga chiqarilgan ba'zi bir tovar yoki xizmatni tushunamiz. Deylik, qo‘lda cheklangan miqdordagi buyumlar bor, n; ularning har birining iste'molchi tomonidan sotib olingan miqdori tovarlar to'plami bilan tavsiflanadi

x= (x 1, x 2, ..., x n),

Bu erda x i iste'molchi tomonidan sotib olingan i-tovar miqdorini bildiradi. Faraz qilamizki, barcha tovarlar o'zboshimchalik bilan bo'linish xususiyatiga ega, shuning uchun ularning har birining har qanday salbiy bo'lmagan miqdorini sotib olish mumkin. U holda barcha mumkin bo'lgan tovar to'plamlari tovarlar makonining vektorlari C = ( x= (x 1, x 2, ..., x n) x i ≥ 0, i = 1, ..., n).

Chiziqli mustaqillik. Tizim e 1 , e 2 , ... , e m n o'lchovli vektorlar deyiladi chiziqli bog'liq agar l 1, l 2, ..., l m raqamlari bo‘lsa, ulardan hech bo‘lmaganda bittasi nolga teng bo‘lib, l 1 bo‘lsin. e 1 + l m e m = 0; aks holda bu vektorlar sistemasi deyiladi chiziqli mustaqil, ya'ni barcha l 1 = l 2 = ... = l m = 0 bo'lgandagina ko'rsatilgan tenglik mumkin bo'ladi. Vektorlarning chiziqli bog'liqligining geometrik ma'nosi R 3, yo'naltirilgan segmentlar sifatida izohlanadi, quyidagi teoremalarni tushuntiring.

Teorema 1. Bitta vektordan tashkil topgan tizim, agar bu vektor nolga teng bo'lsa, chiziqli bog'liqdir.

Teorema 2. Ikki vektor chiziqli bog'liq bo'lishi uchun ularning kollinear (parallel) bo'lishi zarur va etarli.

Teorema 3 ... Uch vektor chiziqli bog'liq bo'lishi uchun ularning koplanar (bir tekislikda yotishi) zarur va etarli.

Vektorlarning chap va o'ng uchliklari. Uchta tekis bo'lmagan vektor a, b, c chaqirdi to'g'ri agar ularning umumiy kelib chiqishidan kuzatuvchi vektorlarning uchlarini kesib o'tsa a, b, c ko'rsatilgan tartibda, u soat yo'nalishi bo'yicha ko'rinadi. Aks holda a, b, c -chap uchlik... Vektorlarning barcha o'ng (yoki chap) uchliklari deyiladi teng yo'naltirilgan.

Bazis va koordinatalar. Troyka e 1, e 2 , e 3 ta koplanar bo'lmagan vektor R 3 deyiladi asos, va vektorlarning o'zlari e 1, e 2 , e 3 - Asosiy... Har qanday vektor a bazis vektorlari bo'yicha yagona kengaytirilishi mumkin, ya'ni shaklda ifodalanadi

a= x 1 e 1 + x 2 e 2 + x 3 e 3, (1.1)

(1.1) kengayishdagi x 1, x 2, x 3 raqamlari chaqiriladi koordinatalara asosda e 1, e 2 , e 3 va belgilangan a(x 1, x 2, x 3).

Ortonormal asos. Agar vektorlar e 1, e 2 , e 3 juft perpendikulyar va ularning har birining uzunligi bittaga teng bo'lsa, asos deyiladi. ortonormal, va koordinatalari x 1, x 2, x 3 - to'rtburchaklar. Ortonormal bazisning bazis vektorlari bilan belgilanadi i, j, k.

Biz buni kosmosda taxmin qilamiz R 3 dekart to'rtburchaklar koordinatalarining to'g'ri tizimi tanlangan (0, i, j, k}.

Vektor mahsuloti.Vektor mahsulotia vektor uchun b vektor deyiladi c, bu quyidagi uchta shart bilan belgilanadi:

1. Vektor uzunligi c vektorlar ustiga qurilgan parallelogramm maydoniga son jihatdan teng a va b, ya'ni
c= | a || b | gunoh ( a^b).

2. Vektor c vektorlarning har biriga perpendikulyar a va b.

3. Vektorlar a, b va c ko'rsatilgan tartibda olingan o'ng uchlik hosil qiladi.

Vektor mahsulot uchun c yozuv kiritiladi c =[ab] yoki
c = a × b.

Agar vektorlar a va b to'g'ri, keyin gunoh ( a ^ b) = 0 va [ ab] = 0, xususan, [ aa] = 0. Birlik vektorlarning vektor mahsuloti: [ ij]=k, [jk] = i, [ki]=j.

Agar vektorlar a va b asosda berilgan i, j, k koordinatalar a(a 1, a 2, a 3), b(b 1, b 2, b 3), keyin

Aralash ish. Ikki vektorning o'zaro ko'paytmasi bo'lsa a va b skalyar uchinchi vektorga ko'paytiriladi c, u holda uchta vektorning bunday mahsuloti deyiladi aralash ish va belgisi bilan belgilanadi a b c.

Agar vektorlar a, b va c asosda i, j, k ularning koordinatalari bilan berilgan
a(a 1, a 2, a 3), b(b 1, b 2, b 3), c(c 1, c 2, c 3), keyin

.

Aralash mahsulot oddiy geometrik talqinga ega - bu mutlaq qiymatda ushbu uchta vektorga qurilgan parallelepiped hajmiga teng skalardir.

Agar vektorlar o'ng tomonli uchlikni tashkil qilsa, u holda ularning aralash mahsuloti ko'rsatilgan hajmga teng ijobiy sondir; agar uchta a, b, c - keyin chapga a b c<0 и V = - a b c, shuning uchun V = | a b c |.

Birinchi bobning masalalarida uchragan vektorlarning koordinatalari to'g'ri ortonormal bazisga nisbatan berilgan deb faraz qilinadi. Vektorga koordinatsiyali birlik vektor a, belgisi bilan belgilanadi a O. Belgi r=OM M nuqtaning radius vektori, a, AB yoki belgilari bilan belgilanadi |a |, |AB | vektor modullari a va AB.

Misol 1.2. Vektorlar orasidagi burchakni toping a= 2m+4n va b= m-n, qayerda m va n - birlik vektorlari va orasidagi burchak m va n 120 p ga teng.

Yechim... Bizda: cos ph = ab/ ab, ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4 + 2cos120 o = - 2 + 2 (-0,5) = -3; a = ; a 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4 + 16 (-0,5) + 16 = 12, shuning uchun a =. b = ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 = 1-2 (-0,5) +1 = 3, shuning uchun b =. Nihoyat, bizda: cos ph == -1/2, ph = 120 o.

1.3-misol. Vektorlarni bilish AB(-3, -2.6) va Miloddan avvalgi(-2,4,4), ABC uchburchakning AD balandligi uzunligini hisoblang.

Yechim... ABC uchburchakning S dan S gacha bo'lgan maydonini belgilab, biz quyidagilarni olamiz:
S = miloddan avvalgi 1/2. Keyin AD = 2S / BC, BC = = = 6,
S = 1/2 | AB ×AC |. AC = AB + BC, shuning uchun vektor AC koordinatalariga ega
.

TA’RIF

Vektor(latdan." vektor"-" rulman ") - kosmosdagi yoki tekislikdagi to'g'ri chiziqning yo'naltirilgan segmenti.

Grafik jihatdan vektor ma'lum uzunlikdagi yo'naltirilgan chiziq segmenti sifatida tasvirlangan. Boshi nuqtada, oxiri esa nuqtada bo'lgan vektor quyidagicha belgilanadi (1-rasm). Shuningdek, vektorni bitta kichik harf bilan belgilash mumkin, masalan,.

Agar koordinatalar tizimi fazoda ko'rsatilgan bo'lsa, u holda vektor uning koordinatalari to'plami bilan yagona aniqlanishi mumkin. Ya'ni vektor deganda kattaligi (uzunligi), yo'nalishi va qo'llanish nuqtasi (vektorning boshlanishi) bo'lgan ob'ekt tushuniladi.

Vektor hisobining boshlanishi 1831 yilda nemis matematigi, mexaniki, fizigi, astronomi va geodezik Iogann Karl Fridrix Gauss (1777-1855) asarlarida paydo bo'ldi. Vektorlar bilan amallar bo'yicha ishlar irland matematigi, mexanik va nazariy fizigi ser Uilyam Rouen Hamilton (1805-1865) tomonidan o'zining kvaternion hisobi doirasida nashr etilgan. Olim "vektor" atamasini taklif qildi va vektorlar ustidagi ba'zi amallarni tavsiflab berdi. Vektor hisobi ingliz fizigi, matematigi va mexaniki Jeyms Klerk Maksvell (1831-1879) tomonidan elektromagnetizm bo'yicha olib borilgan ishlar tufayli yanada rivojlangan. 1880-yillarda amerikalik fizik, fizik-kimyogar, matematik va mexanik Jozia Uillard Gibbs (1839-1903) tomonidan “Vektor tahlilining elementlari” kitobi nashr etilgan. Zamonaviy vektor tahlili 1903 yilda ingliz mustaqil olimi, muhandisi, matematigi va fizigi Oliver Xevisayd (1850-1925) tomonidan tasvirlangan.

TA’RIF

Uzunlik yoki vektor moduli vektorni aniqlaydigan yo'naltirilgan segmentning uzunligi. Sifatida ko'rsatilgan.

Vektorlarning asosiy turlari

Nol vektor boshlang'ich nuqtasi va tugash nuqtasi mos keladigan vektordir. Nol vektorning uzunligi nolga teng.

Bir to'g'ri chiziqqa parallel yoki bitta to'g'ri chiziqda yotgan vektorlar deyiladi kollinear(2-rasm).

hamkorlikda boshqargan agar ularning yo'nalishlari bir xil bo'lsa.

2-rasmda bu vektorlar va. Vektorlarning birgalikdagi yo'nalishi quyidagicha ifodalanadi:.

Ikki kollinear vektor deyiladi qarama-qarshi yo'naltirilgan agar ularning yo'nalishlari qarama-qarshi bo'lsa.

3-rasmda bu vektorlar va. Belgilanishi:.

VEKTORLAR... HARAKATLARYUQORIDAVEKTORLAR. SKALAR,

VEKTOR, VEKTORLARNING ARAŞMA MAHSULOTI.

1. VEKTORLAR, VEKTORLARGA HARAKATLAR.

Asosiy ta'riflar.

Ta'rif 1. Tanlangan birliklar tizimidagi son qiymati bilan to'liq xarakterlanadigan miqdor deyiladi skaler yoki skaler .

(tana vazni, hajmi, vaqti va boshqalar)

Ta'rif 2. Raqamli qiymat va yo'nalish bilan tavsiflangan miqdor deyiladi vektor yoki vektor .

(Silinish, kuch, tezlik va boshqalar)

Belgilar:, yoki,.

Geometrik vektor yo'nalishli chiziqdir.

Vektor uchun - nuqta A- boshlanish, nuqta V- vektorning oxiri.

Ta'rif 3.Modul vektor - AB segmentining uzunligi.

Ta'rif 4. Moduli nolga teng bo'lgan vektor deyiladi nol , tomonidan ko'rsatilgan.

Ta'rif 5. Parallel chiziqlarda yoki bir chiziqda joylashgan vektorlar deyiladi kollinear ... Agar ikkita kollinear vektor bir xil yo'nalishga ega bo'lsa, ular deyiladi hamkorlikda boshqargan .

Ta'rif 6. Ikki vektor hisobga olinadi teng , agar ular hamkorlikda boshqargan va mutlaq qiymatida tengdir.

Vektorlar ustida amallar.

1) Vektorlarni qo'shish.

Def. 6.summasi ikkita vektor va bu vektorlar ustida qurilgan parallelogrammaning diagonali, ularni qo'llashning umumiy nuqtasidan boshlab. (paralelogramma qoidasi).

1-rasm.

Def. 7. Uch vektor yig'indisi,, bu vektorlar ustiga qurilgan parallelepipedning diagonali deyiladi (quti qoidasi).

Def. sakkiz. Agar A, V, BILAN - ixtiyoriy nuqtalar, keyin + = (uchburchak qoidasi).

2-rasm

Qo'shish xususiyatlari.

1 O . + = + (transpozitsiyaviy qonun).

2 O . + (+) = (+) + = (+) + (birlashma qonuni).

3 O . + (– ) + .

2) Vektorlarni ayirish.

Def. 9. ostida farq vektorlar va vektorni tushunish = - shunday + = .

Paralelogrammada bu boshqa diagonal SD (1-rasmga qarang).

3) vektorni songa ko'paytirish.

Def. 10. Mahsulot bo'yicha skalar boshiga vektorlar k vektor deyiladi

= k = k ,

uzoq ka , va qaysi yo'nalish:

1.if vektor yo'nalishiga to'g'ri keladi k > 0;

2.Vektor yo'nalishiga qarama-qarshi, agar k < 0;

3. o‘zboshimchalik bilan, agar k = 0.

Vektorni songa ko'paytirish xossalari.

1 O . (k + l ) = k + l .

k ( + ) = k + k .

2 o . k (l ) = (kl ) .

3 o . 1  = , (–1)  = – , 0  = .

Vektor xossalari.

Def. o'n bir. Ikki vektor va deyiladi kollinear agar ular joylashgan bo'lsa parallel chiziqlar yoki da bitta to'g'ri chiziq.

Null vektor har qanday vektorga kollineardir.

Teorema 1. Ikki nolga teng bo'lmagan vektor va kollinear,  ular proportsional bo'lganda, ya'ni.

= k , k Skayar hisoblanadi.

Def. 12. Uch vektor,, deyiladi koplanar agar ular qandaydir tekislikka parallel bo'lsa yoki unda yotsa.

Teorema 2. Nolga teng bo'lmagan uchta vektor,, tekislik,  ulardan biri qolgan ikkitasining chiziqli birikmasi bo'lsa, ya'ni.

= k + l , k , l - skalyarlar.

Vektorning o'qga proyeksiyasi.

Teorema 3. Vektorning o'qga proyeksiyasi (yo'naltirilgan to'g'ri chiziq) l vektor uzunligi va vektor yo'nalishi va eksa yo'nalishi orasidagi burchakning kosinusining mahsulotiga teng, ya'ni. = a  c os  ,  = ( , l).

2. VEKTOR KOORDINATLARI

Def. o'n uch. Koordinata o'qlaridagi vektor proyeksiyalari Oh, OU, Oz deyiladi vektor koordinatalari. Belgilanishi:  a x , a y , a z .

Vektor uzunligi:

Misol: Vektor uzunligini hisoblang.

Yechim:

Nuqtalar orasidagi masofa va formula bo'yicha hisoblanadi: .

Misol: M (2,3, -1) va K (4,5,2) nuqtalar orasidagi masofani toping.

Koordinata shaklidagi vektorlar ustida amallar.

Berilgan vektorlar =  a x , a y , a z va =  b x , b y , b z .

1. (  )= a x  b x , a y  b y , a z  b z .

2.  =   a x ,  a y ,  a z, qayerda  Skayar hisoblanadi.

Vektorlarning nuqta mahsuloti.

Ta'rifi: Ikki vektorning nuqta mahsuloti ostida va

bu vektorlar uzunliklarining kosinuslari orasidagi burchak kosinusiga teng bo'lgan raqam tushuniladi, ya'ni. = , vektorlar orasidagi burchak va.

Nuqta mahsulotining xususiyatlari:

1.  =

2. ( + ) =

3.

4.

5. , skalyarlar qayerda.

6.ikki vektor perpendikulyar (ortogonal) bo'lsa .

7.agar va faqat agar .

Koordinata shaklidagi nuqta mahsuloti: , qayerda va .

Misol: vektorlarning nuqta mahsulotini toping

Yechim:

Vektor tutuvchi vektorlar.

Ta'rif: Ikki vektorning vektor mahsuloti deganda vektor tushuniladi, buning uchun:

Modul ushbu vektorlarda qurilgan parallelogramm maydoniga teng, ya'ni. , bu erda vektorlar orasidagi burchak va

Bu vektor ko'paytirilayotgan vektorlarga perpendikulyar, ya'ni.

Agar vektorlar kollinear bo'lmasa, ular vektorlarning to'g'ri uchligini hosil qiladi.

Vektor mahsulot xususiyatlari:

(1) Omillar tartibini o'zgartirganda, vektor mahsuloti modulni saqlab, o'z belgisini teskari tomonga o'zgartiradi, ya'ni.

2 .Vektor kvadrati nol vektorga teng, ya'ni.

3 Skayar omil vektor mahsulotining belgisidan tashqariga ko'chirilishi mumkin, ya'ni.

4 Har qanday uchta vektor uchun tenglik

5 Ikki vektorning kollinearligi uchun zarur va etarli shart va:

Koordinata shaklida vektor mahsuloti.

Agar vektorlarning koordinatalari va , u holda ularning o‘zaro ko‘paytmasi quyidagi formula bo‘yicha topiladi:

.

Keyin vektor mahsulotining ta'rifidan kelib chiqadiki, vektorlar ustiga qurilgan parallelogrammning maydoni quyidagi formula bo'yicha hisoblanadi:

Misol: Cho'qqilari (1; -1; 2), (5; -6; 2), (1; 3; -1) bo'lgan uchburchakning maydonini hisoblang.

Yechim: .

Keyin ABC uchburchagining maydoni quyidagicha hisoblanadi:

,

Vektorlarning aralash mahsuloti.

Ta'rifi: Vektorlarning aralash (vektor-skalar) mahsuloti quyidagi formula bo'yicha aniqlangan sondir: .

Aralash ishning xususiyatlari:

1. Aralash mahsulot uning omillarining tsiklik almashinuvi ostida o'zgarmaydi, ya'ni. .

2. Ikki qo'shni omilni almashtirishda aralash mahsulot o'z belgisini teskarisiga o'zgartiradi, ya'ni. ...

3 Uch vektorning mutanosibligi uchun zarur va etarli shart : =0.

4 Uch vektorning aralash mahsuloti bu vektorlar ustida qurilgan parallelepipedning hajmiga teng bo'lib, agar bu vektorlar o'ng uchlikni tashkil qilsa, ortiqcha belgisi bilan olinadi va agar ular chap uchlikni hosil qilsa, minus belgisi bilan olinadi, ya'ni. .

Agar ma'lum bo'lsa koordinatalar vektorlar , u holda aralash ish quyidagi formula bo'yicha topiladi:

Misol: Vektorlarning aralash mahsulotini hisoblang.

Yechim:

3. Vektorlar sistemasining asosi.

Ta'rif. Vektorlar sistemasi deganda bir fazoga mansub bir nechta vektor tushuniladi R.

Izoh. Agar tizim cheklangan miqdordagi vektorlardan iborat bo'lsa, u holda ular turli indeksli bir xil harf bilan belgilanadi.

Misol.

Ta'rif. Formaning har qanday vektori = vektorlarning chiziqli birikmasi deyiladi. Raqamlar chiziqli birikmaning koeffitsientlari.

Misol. .

Ta'rif... Agar vektor vektorlarning chiziqli birikmasi bo'lsa , u holda vektor vektorlar bilan chiziqli ifodalangan deyiladi .

Ta'rif. Vektor sistemasi deyiladi chiziqli mustaqil agar tizim vektorlarining hech biri qolgan vektorlarning chiziqli birikmasi kabi bo'lolmasa. Aks holda, tizim chiziqli bog'liq deb ataladi.

Misol... Vektor tizimi vektordan boshlab chiziqli bog'liq .

Asosni aniqlash. Vektorlar tizimi asos bo'ladi, agar:

1) chiziqli mustaqil,

2) fazoning istalgan vektori u orqali chiziqli ifodalanadi.

1-misol. Kosmik asos:.

2. Vektorlar sistemasida vektorlar asos bo'ladi: vektorlar orqali chiziqli ifodalanadi.

Izoh. Berilgan vektor tizimining asosini topish uchun sizga kerak:

1) vektorlarning koordinatalarini matritsaga yozing;

2) matritsani uchburchak shaklga keltirish uchun elementar transformatsiyalardan foydalanish,

3) matritsaning nolga teng bo'lmagan qatorlari tizimning asosi bo'ladi,

4) bazisdagi vektorlar soni matritsaning darajasiga teng.

uchun vazifalar bo'ladi mustaqil qaror javoblarini ko'rishingiz mumkin.

Vektor tushunchasi

Vektorlar va ular ustida amallar haqida hamma narsani o'rganishdan oldin, oddiy masalani hal qilishni sozlang. Sizning tadbirkorligingiz vektoringiz va innovatsion qobiliyatingiz vektori mavjud. Tadbirkorlik vektori sizni 1-maqsadga, innovatsion qobiliyatlar vektori esa 2-maqsadga olib boradi.O'yin qoidalari shundayki, siz bir vaqtning o'zida bu ikki vektor yo'nalishi bo'yicha harakatlana olmaysiz va bir vaqtning o'zida ikkita maqsadga erisha olmaysiz. Vektorlar o'zaro ta'sir qiladi yoki matematik tilda aytganda, vektorlar ustida qandaydir amallar bajariladi. Ushbu operatsiyaning natijasi sizni 3-maqsadga olib boradigan "Natija" vektoridir.

Endi ayting-chi: "Korxona" va "Innovatsion qobiliyatlar" vektorlari bo'yicha qanday operatsiya natijasi "Natija" vektori? Agar darhol ayta olmasangiz, tushkunlikka tushmang. Ushbu darsni o'tish jarayonida siz ushbu savolga javob bera olasiz.

Yuqorida aytib o'tganimizdek, vektor, albatta, bir nuqtadan ketadi A bir nuqtaga to'g'ri chiziqda B... Shuning uchun har bir vektor nafaqat raqamli qiymatga - uzunlikka, balki jismoniy va geometrik - yo'nalishga ega. Bu vektorning birinchi va eng oddiy ta'rifiga olib keladi. Demak, vektor bu nuqtadan yo'naltirilgan segmentdir A nuqtaga B... U quyidagicha belgilanadi:.

Va boshqacha boshlash uchun vektor operatsiyalari , biz yana bitta vektor ta'rifi bilan tanishishimiz kerak.

Vektor - bu biron bir boshlang'ich nuqtadan erishmoqchi bo'lgan nuqtaning bir turi. Masalan, uch o'lchamli vektor odatda shunday yoziladi (x, y, z) . Oddiy qilib aytganda, bu raqamlar bir nuqtaga borish uchun uch xil yo'nalishda qancha masofani bosib o'tish kerakligini ko'rsatadi.

vektor berilgan bo'lsin. Qayerda x = 3 (o'ng qo'l o'ngga ishora qiladi) y = 1 (chap qo'l oldinga ishora qiladi) z = 5 (nuqta ostida yuqoriga ko'tariladigan zinapoya bor). Ushbu ma'lumotlarga ko'ra, siz o'ng qo'l bilan ko'rsatilgan yo'nalishda 3 metr, keyin chap qo'l bilan ko'rsatilgan yo'nalishda 1 metr yurib, bir nuqtani topasiz, keyin sizni zinapoya kutmoqda va 5 metrga ko'tarilib, siz nihoyat bo'lasiz. O'zingizni oxirgi nuqtada toping.

Boshqa barcha atamalar vektorlar ustida turli operatsiyalar, ya'ni amaliy muammolarni hal qilish uchun zarur bo'lgan yuqoridagi tushuntirishning takomillashtirilishi. Keling, tipik vektor muammolariga to'xtalib, ushbu qat'iy ta'riflarni ko'rib chiqaylik.

Jismoniy misollar vektor kattaliklari fazoda harakatlanuvchi moddiy nuqtaning siljishi, bu nuqtaning tezligi va tezlanishi, shuningdek, unga ta'sir qiluvchi kuch bo'lishi mumkin.

Geometrik vektor shaklida ikki o'lchovli va uch o'lchovli fazoda taqdim etilgan yo'nalishli segment... Bu boshi va oxirini ajratib turadigan segment.

Agar A vektorning boshlanishi, va B- uning oxiri, keyin vektor belgi yoki bitta kichik harf bilan belgilanadi. Rasmda vektorning oxiri o'q bilan ko'rsatilgan (1-rasm).

Uzunlik(yoki modul) geometrik vektorning uni hosil qiluvchi segment uzunligi

Ikki vektor deyiladi teng , agar ular parallel uzatish yo'li bilan (agar yo'nalishlar mos keladigan bo'lsa) hizalanishi mumkin bo'lsa, ya'ni. agar ular parallel bo'lsa, bir xil yo'nalishga ishora qiling va teng uzunliklarga ega.

Fizikada bu ko'pincha ko'rib chiqiladi biriktirilgan vektorlar qo'llash nuqtasi, uzunligi va yo'nalishi bilan berilgan. Agar vektorni qo'llash nuqtasi muhim bo'lmasa, u holda u kosmosning istalgan nuqtasiga uzunligi va yo'nalishini saqlab, o'tkazilishi mumkin. Bunday holda vektor chaqiriladi ozod... Biz faqat ko'rib chiqishga rozi bo'lamiz bepul vektorlar.

Geometrik vektorlar ustida chiziqli amallar

Vektorni raqamga ko'paytirish

Vektor mahsuloti raqami bo'yicha vektordan vaqtlar bo'yicha kengayish (at) yoki siqilish (at) yo'li bilan olingan vektor deyiladi va vektorning yo'nalishi saqlanib qoladi, agar, va aksincha, agar o'zgaradi. (2-rasm)

Ta'rifdan kelib chiqadiki, vektorlar va = har doim bitta yoki parallel chiziqlar ustida joylashgan. Bunday vektorlar deyiladi kollinear... (Bu vektorlarni parallel deb ham aytishingiz mumkin, lekin vektor algebrasida "kollinear" deyish odat tusiga kiradi.) Buning aksi ham to'g'ri: vektorlar va kollinear bo'lsa, ular munosabat bilan bog'lanadi.

Demak, tenglik (1) ikkita vektor uchun kollinearlik shartini ifodalaydi.

Vektorlarni qo'shish va ayirish

Vektorlarni qo'shishda siz buni bilishingiz kerak so'm vektorlar va vektor deb ataladi, uning boshlanishi vektorning boshiga, oxiri esa vektorning oxiriga to'g'ri keladi, agar vektorning boshi vektor oxiriga biriktirilgan bo'lsa. (3-rasm)

Ushbu ta'rif har qanday chekli vektor soniga taqsimlanishi mumkin. Bo'sh joy berilsin n bepul vektorlar. Bir nechta vektorlarni qo'shganda, yopilish vektori ularning yig'indisi sifatida olinadi, uning boshlanishi birinchi vektorning boshiga, oxiri esa oxirgi vektorning oxiriga to'g'ri keladi. Ya'ni vektorning boshini vektor oxiriga, vektorning boshini esa vektor oxiriga biriktirsangiz va hokazo. va, nihoyat, vektorning oxirigacha - vektorning boshi, keyin bu vektorlarning yig'indisi yopish vektoridir. uning boshlanishi birinchi vektorning boshiga, oxiri esa oxirgi vektorning oxiriga to'g'ri keladi. (4-rasm)

Terminlar vektorning komponentlari deb ataladi va tuzilgan qoida ko'pburchak qoidasi... Bu ko'pburchak tekis bo'lmasligi mumkin.

Vektorni -1 ga ko'paytirsangiz, qarama-qarshi vektorni olasiz. vektorlari bir xil uzunlikka va qarama-qarshi yo'nalishga ega. Ularning summasi beradi nol vektor uzunligi nolga teng. Nol vektorning yo'nalishi aniqlanmagan.

Vektor algebrasida ayirish operatsiyasini alohida ko'rib chiqishning hojati yo'q: vektordan vektorni ayirish vektorga qarama-qarshi vektorni qo'shishni anglatadi, ya'ni.

1-misol. Ifodani soddalashtiring:

.

,

ya'ni vektorlarni ko'phadlar kabi raqamlarga qo'shish va ko'paytirish mumkin (xususan, ifodalarni soddalashtirish bo'yicha topshiriqlar ham). Odatda, vektorlar mahsulotini hisoblashdan oldin chiziqli o'xshash ifodalarni vektorlar bilan soddalashtirish zarurati tug'iladi.

2-misol. vektorlari va ABCD parallelogrammaning diagonallari vazifasini bajaradi (4a-rasm). Ushbu parallelogrammning tomonlari bo'lgan ikkala vektor va, ifodasi bilan ifodalang.

Yechim. Paralelogramma diagonallarining kesishish nuqtasi har bir diagonalni yarmiga bo'ladi. Biz muammo bayonida talab qilinadigan vektorlarning uzunliklarini yoki keraklilari bilan uchburchak hosil qiluvchi vektorlar yig‘indisining yarmi yoki farqlarning yarmi (diogonal bo‘lib xizmat qiluvchi vektor yo‘nalishiga qarab) yoki quyidagicha topamiz. ikkinchi holatda, minus belgisi bilan olingan summaning yarmi. Natijada muammo bayonotida talab qilinadigan vektorlar:

Siz ushbu darsning boshida tadbirkorlik va innovatsion qobiliyat vektorlari haqidagi savolga to'g'ri javob berdingiz deb ishonish uchun barcha asoslar mavjud. To'g'ri javob: bu vektorlarda qo'shish amali bajariladi.

Vektorli muammolarni o'zingiz hal qiling va keyin echimlarni ko'ring

Vektorlar yig'indisining uzunligini qanday topish mumkin?

Bu vazifa vektor operatsiyalarida alohida o'rin tutadi, chunki u trigonometrik xususiyatlardan foydalanishni o'z ichiga oladi. Aytaylik, siz quyidagi kabi vazifaga duch keldingiz:

Vektorlarning uzunliklari berilgan va bu vektorlar yig'indisining uzunligi. Ushbu vektorlar orasidagi farq uzunligini toping.

Bu va boshqalar uchun echimlar shunga o'xshash vazifalar va ularni qanday hal qilish haqida tushuntirish - darsda " Vektor qo'shish: vektor yig'indisi uzunligi va kosinus teoremasi ".

Va siz bunday muammolarning echimini tekshirishingiz mumkin Onlayn kalkulyator "Uchburchakning noma'lum tomoni (vektorlarni qo'shish va kosinuslar teoremasi)" .

Vektorlarning hosilalari qayerda?

Vektorli vektorli mahsulotlar chiziqli operatsiyalar emas va alohida ko'rib chiqiladi. Va bizda vektorlarning nuqta mahsuloti va vektorlarning vektorlarning aralash mahsuloti darsliklari mavjud.

Vektorning o'qga proyeksiyasi

Vektorning o'qga proyeksiyasi proyeksiyalangan vektor uzunligining vektor va o'q orasidagi burchak kosinusiga ko'paytmasiga teng:

Ma'lumki, nuqtaning proyeksiyasi A to'g'ri chiziqda (tekislikda) bu nuqtadan to'g'ri chiziqqa (tekislik) tushirilgan perpendikulyar asosdir.

Ixtiyoriy vektor bo'lsin (5-rasm) va uning boshlanishi (nuqtalari) proyeksiyalari bo'lsin. A) va oxiri (nuqtalar B) har bir eksa l... (Nuqtaning proyeksiyasini qurish uchun A) nuqtadan o'tgan to'g'ri chiziqda A to'g'ri chiziqqa perpendikulyar tekislik. Chiziq va tekislikning kesishishi kerakli proyeksiyani aniqlaydi.

Vektor komponenti l o'qi bo'yicha bu o'qda yotuvchi vektor deb ataladi, uning boshlanishi boshlang'ich proyeksiyasiga, oxiri esa vektor oxirining proyeksiyasiga to'g'ri keladi.

Vektorning o'qga proyeksiyasi l raqamga qo'ng'iroq qildi

,

komponentlar yo'nalishi eksa yo'nalishiga to'g'ri keladigan bo'lsa, ortiqcha belgisi bilan olingan ushbu o'qdagi komponent vektorining uzunligiga teng. l, va agar bu yo'nalishlar qarama-qarshi bo'lsa, minus belgisi bilan.

Eksadagi vektor proyeksiyalarining asosiy xossalari:

1. Bir o'qdagi teng vektorlarning proyeksiyalari bir-biriga teng.

2. Vektorni songa ko'paytirishda uning proyeksiyasi bir xil songa ko'paytiriladi.

3. Har qanday o‘qdagi vektorlar yig‘indisining proyeksiyasi bir xil o‘qdagi vektorlar yig‘indilarining proyeksiyalari yig‘indisiga teng.

4. Vektorning o'qga proyeksiyasi proyeksiyalangan vektor uzunligini vektor va o'q orasidagi burchak kosinusiga ko'paytmasiga teng:

.

Yechim. Vektorlarni o'qga loyihalash l yuqoridagi nazariy asosda aniqlanganidek. 5a-rasmdan ko'rinib turibdiki, vektorlar yig'indisining proyeksiyasi vektorlar proyeksiyalarining yig'indisiga teng. Ushbu prognozlarni hisoblaymiz:

Vektorlar yig‘indisining yakuniy proyeksiyasini toping:

Vektorning fazoda to'rtburchak dekart koordinatalar sistemasi bilan aloqasi

Bilan tanishish fazodagi to'rtburchak Dekart koordinatalar tizimi tegishli darsda bo'lib o'tdi, uni yangi oynada ochish ma'qul.

Tartiblangan koordinatalar tizimida 0xyz o'qi ho'kiz chaqirdi abscissa, eksa 0y – y o'qi, va eksa 0z – eksa qo'llaniladi.

Ixtiyoriy nuqta bilan M biz vektor bilan bog'laydigan fazo

chaqirdi radius vektori ball M va uni koordinata o'qlarining har biriga proyeksiyalang. Tegishli proyeksiyalarning qiymatlarini belgilaymiz:

Raqamlar x, y, z deyiladi M nuqtaning koordinatalari, mos ravishda abscissa, ordinata va ariza berish, va raqamlarning tartiblangan nuqtasi sifatida yoziladi: M (x; y; z)(6-rasm).

Yo'nalishi o'qning yo'nalishiga to'g'ri keladigan birlik uzunlikdagi vektor deyiladi birlik vektor(yoki ortom) o'qi. bilan belgilaymiz

Shunga ko'ra, koordinata o'qlarining birlik vektorlari ho'kiz, Oy, Oz

Teorema. Har qanday vektorni koordinata o'qlarining birlik vektorlari bo'ylab kengaytirish mumkin:

(2)

Tenglik (2) vektorning koordinata o'qlari bo'ylab kengayishi deyiladi. Ushbu kengayish koeffitsientlari vektorning koordinata o'qlariga proyeksiyalari hisoblanadi. Shunday qilib, vektorning koordinata o'qlari bo'ylab kengayish koeffitsientlari (2) vektorning koordinatalari.

Kosmosda ma'lum bir koordinatalar tizimini tanlagandan so'ng, vektor va uning koordinatalarining uchligi bir-birini yagona tarzda aniqlaydi, shuning uchun vektorni ko'rinishda yozish mumkin.

(2) va (3) ko'rinishdagi vektorning ko'rinishlari bir xil.

Koordinatadagi vektorlar uchun kollinearlik sharti

Yuqorida aytib o'tganimizdek, vektorlar, agar ular munosabat bilan bog'langan bo'lsa, ular kollinear deyiladi

Vektorlar bo'lsin ... Agar vektorlarning koordinatalari munosabat bilan bog'langan bo'lsa, bu vektorlar kollineardir

,

ya'ni vektorlarning koordinatalari proporsionaldir.

6-misol. Berilgan vektorlar ... Bu vektorlar kollinearmi?

Yechim. Ushbu vektorlarning koordinatalarining nisbatini aniqlaymiz:

.

Vektorlarning koordinatalari proportsionaldir, shuning uchun vektorlar kollinear yoki bir xil bo'lgan paralleldir.

Vektor uzunligi va yo'nalishi kosinuslari

Koordinata o'qlarining o'zaro perpendikulyarligi tufayli vektor uzunligi

vektorlar ustida qurilgan to'rtburchaklar parallelepiped diagonalining uzunligiga teng

va tenglik bilan ifodalanadi

(4)

Vektor ikkita nuqtani (boshi va oxiri) ko'rsatish orqali to'liq aniqlanadi, shuning uchun vektorning koordinatalarini ushbu nuqtalarning koordinatalari bilan ifodalash mumkin.

Berilgan koordinatalar sistemasida vektorning kelib chiqishi nuqtada bo'lsin

va oxiri nuqtada

Tenglikdan

Bunga amal qiladi

yoki koordinatali shaklda

Demak, vektorning koordinatalari vektorning oxiri va boshi bir xil nomdagi koordinatalarning farqiga teng ... Formula (4) bu holda shaklni oladi

Vektorning yo'nalishi bilan belgilanadi yo'nalish kosinuslari ... Bu vektor o'qlar bilan hosil qiladigan burchaklarning kosinuslari ho'kiz, Oy va Oz... Bu burchaklarni navbati bilan belgilaylik α , β va γ ... Keyin bu burchaklarning kosinuslarini formulalar orqali topish mumkin

Vektorning yo'nalishli kosinuslari ham ushbu vektorning birlik vektorining koordinatalari va demak, vektor vektoridir.

.

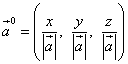
Vektor birligining uzunligi bir birlikka teng ekanligini hisobga olsak, ya'ni

,

yo'nalish kosinuslari uchun quyidagi tenglikni olamiz:

7-misol. Vektor uzunligini toping x = (3; 0; 4).

Yechim. Vektorning uzunligi

8-misol. Ballar beriladi:

Bu nuqtalarda qurilgan uchburchakning teng yonli ekanligini aniqlang.

Yechim. (6) vektor uzunligi formulasidan foydalanib, tomonlarning uzunliklarini topamiz va ular orasida ikkita teng bor yoki yo'qligini aniqlaymiz:

Ikkita teng tomon topildi, shuning uchun uchinchi tomonning uzunligini izlashning hojati yo'q va berilgan uchburchak teng yonlidir.

9-misol. Agar vektor uzunligini va uning yo'nalishi kosinuslarini toping .

Yechim. Vektor koordinatalari berilgan:

.

Vektorning uzunligi kvadrat ildiz vektor koordinatalari kvadratlari yig'indisidan:

.

Yo'nalish kosinuslarini toping:

Vektor muammosini o'zingiz hal qiling va keyin yechimni ko'ring

Koordinata shaklida ko'rsatilgan vektorlar ustida amallar

Ikki vektor berilgan va ularning proyeksiyalari bilan berilgan:

Keling, ushbu vektorlarda amallarni ko'rsatamiz.

Yaratilgan sana: 2009-04-11 15:25:51
Oxirgi tahrir: 2012-02-08 09:19:45

Uzoq vaqt davomida men ushbu maqolani yozishni xohlamadim - materialni qanday taqdim etishni o'ylardim. Bundan tashqari, rasm chizishingiz kerak. Ammo, ko'ryapsizmi, yulduzlar bugungi kunda muvaffaqiyatli shakllangan va vektorlar haqida maqola bo'ladi. Garchi, bu shunchaki qo'pol qoralama. Kelajakda men ushbu maqolani bir nechta alohida maqolalarga ajrataman - etarli material mavjud. Bundan tashqari, maqola asta-sekin yaxshilanadi: men unga o'zgartirishlar kiritaman. bir o‘tirishda barcha jihatlarni ochib bo‘lmaydi.

Vektorlar matematikaga XIX asrda skalyar qiymatlar yordamida tasvirlash qiyin bo‘lgan miqdorlarni tasvirlash uchun kiritilgan.

Vektorlar kompyuter o'yinlarini ishlab chiqishda keng qo'llaniladi. Ular nafaqat an'anaviy ravishda - kuch yoki tezlik kabi miqdorlarni tasvirlash uchun, balki vektorlar bilan hech qanday aloqasi yo'q ko'rinadigan joylarda ham qo'llaniladi: rangni saqlash, soyalarni yaratish.

Skalar va vektorlar

Birinchidan, skalar nima ekanligini va u vektordan qanday farq qilishini eslatib o'taman.

Skalyar qiymatlar ma'lum miqdorni saqlaydi: massa, hajm. Ya'ni, bu faqat bitta raqam (masalan, biror narsaning miqdori) bilan tavsiflangan shaxsdir.

Vektor, skalerdan farqli o'laroq, ikkita qiymat yordamida tavsiflanadi: kattalik va yo'nalish.

Vektorlar va koordinatalar o'rtasidagi muhim farq: vektorlar ma'lum bir joyga bog'lanmagan! Yana bir bor vektordagi asosiy narsa uzunlik va yo'nalishdir.

Vektor lotin alifbosining qalin harfi bilan belgilanadi. Masalan: a, b, v.

Birinchi rasmda vektorning tekislikda qanday belgilanishini ko'rishingiz mumkin.

Kosmosdagi vektorlar

Kosmosda vektorlarni koordinatalar yordamida ifodalash mumkin. Lekin birinchi navbatda siz bitta kontseptsiyani kiritishingiz kerak:

Nuqta radiusi vektori

Fazoda qandaydir M (2,1) nuqtani oling. Nuqtaning radius vektori koordinata boshidan boshlanib, nuqtada tugaydigan vektordir.

Bu erda bizda vektordan boshqa narsa yo'q OM... Vektor boshlanish koordinatalari (0,0), yakuniy koordinatalari (2,1). Bu vektorni quyidagicha belgilaymiz a.

Bu holda vektorni quyidagicha yozish mumkin a = <2, 1>... Bu vektorning koordinata shakli a.

Vektorning koordinatalari o'qlarga nisbatan uning komponentlari deyiladi. Masalan, 2 vektor komponentidir a x o'qi haqida.

Keling, nuqta koordinatalari nima ekanligini yana bir bor ko'rib chiqaylik. Nuqtaning koordinatasi (masalan, x) nuqtaning o'qga proyeksiyasi, ya'ni. perpendikulyarning asosi bir nuqtadan o'qga tushdi. Bizning misolimizda, 2.

Ammo birinchi rasmga qaytaylik. Bu erda ikkita A va B nuqta bor. Nuqtalarning koordinatalari (1,1) va (3,3) bo'lsin. Vektor v bu holda quyidagicha belgilanishi mumkin v = <3-1, 3-1>... Uch o'lchovli fazoda ikki nuqtada joylashgan vektor quyidagicha ko'rinadi:

v =

Menimcha, bu erda hech qanday qiyinchiliklar yo'q.

Vektorni skalerga ko'paytirish

Vektorni skalyar qiymatlarga ko'paytirish mumkin:

k v = =

Bu vektorning har bir komponenti bilan skalyar qiymatni ko'paytiradi.

Agar k> 1 bo'lsa, vektor ortadi, agar k birdan kichik, lekin noldan katta bo'lsa, vektor uzunligi qisqaradi. Agar k noldan kichik bo'lsa, vektor yo'nalishini o'zgartiradi.

Birlik vektorlari

Birlik vektorlari uzunligi birga teng vektorlardir. Koordinatali vektorga e'tibor bering<1,1,1>biriga teng bo'lmaydi! Vektor uzunligini topish quyida matnda tasvirlangan.

Birlik vektorlari deb ataladiganlar mavjud - bular koordinata o'qlari yo'nalishi bo'yicha mos keladigan birlik vektorlari. i- x o'qining birlik vektori, j- y o'qining birlik vektori, k z o'qining birlik vektori.

Qayerda i = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

Endi biz vektorni skalerga ko'paytirish nima ekanligini va birlik vektorlar nima ekanligini bilamiz. Endi biz yozishimiz mumkin v vektor shaklida.

v= v x i+ v y j+ v z k, bu yerda v x, v y, v z vektorning mos keladigan komponentlari

Vektor qo'shilishi

Oldingi formulani to'liq tushunish uchun vektor qo'shish qanday ishlashini tushunishingiz kerak.

Bu erda hamma narsa oddiy. Ikki v1 = vektorini oling va v 2 =

v 1 + v 2 =

Biz faqat ikkita vektorning mos keladigan komponentlarini qo'shmoqdamiz.

Farqi xuddi shu tarzda hisoblab chiqiladi.

Bu matematik shaklga tegishli. To'liqlik uchun vektorlarni qo'shish va ayirish qanday ko'rinishini ko'rib chiqishga arziydi.

Ikki vektor qo'shish uchun a+b... Vektorning boshiga mos kelishingiz kerak b va vektorning oxiri a... Keyin vektorning boshlanishi o'rtasida a va vektorning oxiri b yangi vektor chizish. Aniqlik uchun ikkinchi rasmga qarang ("a" harfi).

Vektorlarni ayirish uchun ikkita vektorning boshlanishini birlashtirib, ikkinchi vektorning oxiridan birinchi vektorning oxirigacha yangi vektor chizishingiz kerak. Ikkinchi rasm ("b" harfi) qanday ko'rinishini ko'rsatadi.

Vektor uzunligi va yo'nalishi

Keling, avval uzunligini ko'rib chiqaylik.

Uzunlik - yo'nalishni hisobga olmaganda, vektorning raqamli qiymati.

Uzunlik formula bo'yicha aniqlanadi (uch o'lchovli vektor uchun):

vektor komponentlari kvadratlari yig'indisining kvadrat ildizi.

Tanish formula, shunday emasmi? Umuman olganda, bu segment uzunligi uchun formuladir

Vektorning yo'nalishi vektor va koordinata o'qlari o'rtasida hosil bo'lgan burchaklarning yo'nalish kosinuslari bilan aniqlanadi. Yo'nalish kosinuslarini topish uchun mos keladigan komponentlar va uzunlikdan foydalaniladi (rasm keyinroq bo'ladi).

Dasturlarda vektorlarni ifodalash

Vektorlarni dasturlarda ifodalashning turli usullari mavjud. Samarali bo'lmagan oddiy o'zgaruvchilar yordamida ham, massivlar, sinflar va tuzilmalar yordamida ham.

Float vektor3 = (1,2,3); // vektor strukturasini saqlash uchun massiv3 // vektorlarni saqlash uchun struktura (float x, y, z;);

Vektorlarni saqlash uchun eng katta imkoniyatlar sinflar tomonidan taqdim etiladi. Darslarda biz faqat vektorning o'zini (o'zgaruvchilari) emas, balki vektor operatsiyalarini (funktsiyalarini) ham tasvirlashimiz mumkin.

Vektorlarning nuqta mahsuloti

Vektorni ko'paytirishning ikki turi mavjud: vektor va skaler.

Nuqta mahsulotining o'ziga xos xususiyati shundaki, natijada har doim skaler qiymat bo'ladi, ya'ni. raqam.

Bu erda quyidagi nuqtaga e'tibor qaratish lozim. Agar ushbu operatsiyaning natijasi nolga teng bo'lsa, u holda ikkita vektor perpendikulyar - ular orasidagi burchak 90 daraja. Natija noldan katta bo'lsa, burchak 90 darajadan past bo'ladi. Agar natija noldan kichik bo'lsa, burchak 90 darajadan kattaroqdir.

Ushbu operatsiya quyidagi formula bilan ifodalanadi:

a · b= a x * b x + a y * b y + a z * b z

Nuqta mahsuloti ikkita vektorning mos keladigan komponentlari ko'paytmalarining yig'indisidir. Bular. Ikki vektorning x "s" ni oling, ularni ko'paytiring, keyin ularni y" s ko'paytmasi bilan qo'shing va hokazo.

Vektorlarning vektor mahsuloti

Ikki vektorning vektor mahsuloti bu vektorlarga perpendikulyar vektor hosil qiladi.

a x b =

Biz bu formulani hali batafsil muhokama qilmaymiz. Qolaversa, eslab qolish juda qiyin. Determinantlar bilan tanishganimizdan so'ng, bu nuqtaga qaytamiz.

Xo'sh, umumiy rivojlanish uchun, natijada olingan vektorning uzunligi vektorlarga qurilgan parallelogrammning maydoniga teng ekanligini bilish foydalidir. a va b.

Vektor normalizatsiyasi

Normallashtirilgan vektor - uzunligi bitta bo'lgan vektor.

Normallashtirilgan vektorni topish formulasi quyidagicha - vektorning barcha komponentlarini uning uzunligiga bo'lish kerak:

v n = v/ | v | =

Keyingi so'z

Ko'rganingizdek, vektorlarni tushunish qiyin emas. Biz bir qancha vektor operatsiyalarini ko'rib chiqdik.

"Matematika" bo'limining keyingi maqolalarida matritsalar, determinantlar, tizimlar haqida gaplashamiz chiziqli tenglamalar... Bu hammasi nazariya.

Shundan so'ng biz matritsalarni o'zgartirishni ko'rib chiqamiz. Aynan o'shanda siz matematika kompyuter o'yinlarini yaratishda qanchalik muhimligini tushunasiz. Bu mavzu avvalgi barcha mavzular uchun amaliyotga aylanadi.