Вектор. Основні властивості

Визначення Упорядковану сукупність (x 1 , x 2 , ... , x n) n дійсних чисел називають n-вимірним вектором, А числа x i (i = 1, ..., n) - компонентами,або координатами,

приклад. Якщо, наприклад, деякий автомобільний завод має випустити у зміну 50 легкових автомобілів, 100 вантажних, 10 автобусів, 50 комплектів запчастин для легкових автомобілів та 150 комплектів для вантажних автомобілів та автобусів, то виробничу програму цього заводу можна записати у вигляді вектора (50, 100 10, 50, 150), що має п'ять компонент.

Позначення. Вектори позначають жирними малими літерами або літерами з рисою або стрілкою вгорі, наприклад, aабо . Два вектори називаються рівнимиякщо вони мають однакову кількість компонентів і їх відповідні компоненти рівні.

Компоненти вектора не можна змінювати місцями, наприклад, (3, 2, 5, 0, 1) та (2, 3, 5, 0, 1) різні вектори.
Операції над векторами.Творомx= (x 1 , x 2 , ... ,x n) на дійсне число називається вектор λ x= (λ x 1, x 2, ..., x n).

Сумоюx= (x 1, x 2, ..., x n) і y= (y 1 , y 2 , ... ,y n) називається вектор x + y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

Векторні простір. N-мірний векторний простір R n визначається як безліч всіх n-мірних векторів, для яких визначено операції множення на дійсні числа та додавання.

Економічна ілюстрація. Економічна ілюстрація n-вимірного векторного простору: простір благ (товарів). Під товаромми розумітимемо деяке благо чи послугу, що надійшли у продаж у певний час у певному місці. Припустимо, що є кінцеве число готівкових товарів n; кількості кожного з них, придбані споживачем, характеризуються набором товарів

x= (x 1, x 2, ..., x n),

де через x i позначається кількість i-го блага, набутого споживачем. Будемо вважати, що всі товари мають властивість довільної ділимості, так що може бути куплено будь-яку невід'ємну кількість кожного з них. Тоді всі можливі набори товарів є векторами простору товарів C = ( x= (x 1, x 2, ..., x n) x i ≥ 0, i = 1, ..., n).

Лінійна незалежність. Система e 1 , e 2 , ... , e m n-вимірних векторів називається лінійно залежноюякщо знайдуться такі числа λ 1 , λ 2 , ... , λ m , з яких хоча б одне відмінно від нуля, що виконується рівність λ 1 e 1 + λ m e m = 0; в іншому випадку дана система векторів називається лінійно незалежною, тобто зазначена рівність можлива лише у випадку, коли всі 1 = 2 = ... = m =0. Геометричний зміст лінійної залежності векторів R 3 , що інтерпретуються як спрямовані відрізки, пояснюють такі теореми.

Теорема 1. Система, що складається з одного вектора, лінійно залежить тоді і тільки тоді, коли цей вектор нульовий.

Теорема 2. Для того щоб два вектори були лінійно залежні, необхідно і достатньо, щоб вони були колінеарні (паралельні).

Теорема 3 . Для того щоб три вектори були лінійно залежні, необхідно і достатньо, щоб вони були компланарні (лежали в одній площині).

Ліва та права трійки векторів. Трійка некомпланарних векторів a, b, cназивається правою, якщо спостерігачеві з їхнього загального початку обхід кінців векторів a, b, cу вказаному порядку здається таким, що відбувається за годинниковою стрілкою. В іншому випадку a, b, c -ліва трійка. Усі праві (або ліві) трійки векторів називаються однаково орієнтованими.

Базис та координати. Трійка e 1, e 2 , e 3 некомпланарних векторів у R 3 називається базисом, а самі вектори e 1, e 2 , e 3 - базисними. Будь-який вектор aможе бути єдиним чином розкладений за базовими векторами, тобто представлений у вигляді

а= x 1 e 1 + x 2 e 2 + x 3 e 3, (1.1)

числа x 1 , x 2 , x 3 у розкладанні (1.1) називаються координатамиaу базисі e 1, e 2 , e 3 і позначаються a(x 1, x 2, x 3).

Ортонормований базис. Якщо вектори e 1, e 2 , e 3 попарно перпендикулярні і довжина кожного з них дорівнює одиниці, то базис називається ортонормованим, а координати x 1 x 2 x 3 - прямокутними.Базисні вектори ортонормованого базису позначатимемо i, j, k.

Припускатимемо, що в просторі R 3 обрана права система декартових прямокутних координат (0, i, j, k}.

Векторний витвір.Векторним творомана вектор bназивається вектор c, який визначається такими трьома умовами:

1. Довжина вектора cчисельно дорівнює площі паралелограма, побудованого на векторах aі b,тобто.
c= |a||b| sin ( a^b).

2. Вектор cперпендикулярний до кожного з векторів aі b.

3. Вектори a, bі c, взяті у вказаному порядку, утворюють праву трійку

Для векторного твору cвводиться позначення c =[ab] або
c = a × b.

Якщо вектори aі bколінеарні, то sin( a^b) = 0 і [ ab] = 0, зокрема, [ aa] = 0. Векторні твори ортів: [ ij]=k, [jk] = i, [ki]=j.

Якщо вектори aі bзадані у базисі i, j, kкоординатами a(a 1 , a 2 , a 3), b(b 1, b 2, b 3), то

Змішаний твір. Якщо векторний твір двох векторів аі bскалярно множиться на третій вектор c,то такий твір трьох векторів називається змішаним творомі позначається символом a b c.

Якщо вектори a, bі cу базисі i, j, kзадані своїми координатами
a(a 1 , a 2 , a 3), b(b 1, b 2, b 3), c(c 1 , c 2 , c 3), то

.

Змішаний твір має просте геометричне тлумачення - це скаляр, по абсолютній величині, рівний об'єму паралелепіпеда, побудованого на трьох даних векторах.

Якщо вектори утворюють праву трійку, їх змішаний твір є число позитивне, рівне зазначеному обсягу; якщо ж трійка a, b, c -ліва, то a b c<0 и V = - a b c, отже V = |a b c|.

Координати векторів, що зустрічаються у задачах першого розділу, передбачаються заданими щодо правого ортонормованого базису. Поодинокий вектор, спрямований вектор а,позначається символом ао. Символом r=ОМпозначається радіус-вектор точки М, символами а, АВ або |а|, |АВ|позначаються модулі векторів аі АВ.

приклад 1.2. Знайдіть кут між векторами a= 2m+4nі b= m-n, де mі n -одиничні вектори та кут між mі nдорівнює 120 о.

Рішення. Маємо: cos φ = ab/ab, ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4+2cos120 o = - 2 + 2(-0.5) = -3; a = ; a 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4+16(-0.5)+16=12, отже a = . b = ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 = 1-2(-0.5)+1 = 3, отже b = . Остаточно маємо: cos = = -1/2, = 120 o .

приклад 1.3.Знаючи вектори AB(-3,-2,6) та BC(-2,4,4), обчисліть довжину висоти AD трикутника ABC.

Рішення. Позначаючи площу трикутника ABC через S, отримаємо:
S = 1/2 BC AD. Тоді AD=2S/BC, BC= = = 6,
S = 1/2 | AB ×AC|. AC=AB+BCотже, вектор ACмає координати
.

ВИЗНАЧЕННЯ

Вектор(Від лат. « vector» – «несучий») – спрямований відрізок прямий у просторі чи площині.

Графічно вектор зображується як спрямованого відрізка прямої певної довжини. Вектор, початок якого в точці , а кінець – у точці , позначається як (рис. 1). Також вектор можна позначати однією маленькою літерою, наприклад .

Якщо просторі задана система координат, то вектор можна однозначно задати набором своїх координат. Тобто під вектором розуміється об'єкт, який має величину (довжину), напрямок та точку застосування (початок вектора).

Початки векторного обчислення з'явилися в роботах 1831 року в роботах німецького математика, механіка, фізика, астронома та геодезиста Йоганна Карла Фрідріха Гауса (1777-1855). Роботи, присвячені операціям із векторами, опублікував ірландський математик, механік та фізик-теоретик, сер Вільям Роуен Гамільтон (1805-1865) у рамках свого кватерніонного обчислення. Вчений запропонував термін «вектор» та описав деякі операції над векторами. Векторне обчислення отримало свій розвиток завдяки роботам з електромагнетизму британського фізика, математика і механіка Джеймса Клерка Максвелла (1831-1879). У 1880-х роках побачила світ книга «Елементи векторного аналізу» американського фізика, фізикохіміка, математика та механіка Джозайя Уілларда Гіббса (1839–1903). Сучасний векторний аналіз був описаний в 1903 в роботах англійського вченого-самоучки, інженера, математика і фізика Олівера Хевісайда (1850-1925).

ВИЗНАЧЕННЯ

Довжиноюабо модулем вектораназивається довжина спрямованого відрізка, що визначає вектор. Позначається як .

Основні види векторів

Нульовим векторомназивається вектор , у якого початкова точка та кінцева точка збігаються. Довжина нульового вектора дорівнює нулю.

Вектори, паралельні одній прямій або лежать на одній прямій, називають колінеарними(Рис. 2).

співспрямованимиякщо їх напрями збігаються.

На малюнку 2 – це вектори та . Сонаправленность векторів позначається так: .

Два колінеарних вектори називаються протилежно спрямованими, якщо їх напрями протилежні.

На малюнку 3 – це вектори та . Позначення: .

ВЕКТОРИ. ДІЇНАДВЕКТОРАМИ. СКАЛЯРНЕ,

ВЕКТОРНИЙ, ЗМІШАНИЙ ТВОР ВЕКТОРІВ.

1. ВЕКТОРИ, ДІЇ НАД ВЕКТОРАМИ.

Основні визначення.

Визначення 1.Величина, що повністю характеризується своїм числовим значенням у вибраній системі одиниць, називається скалярноїабо скаляром .

(Маса тіла, об'єм, час тощо)

Визначення 2.Величина, що характеризується числовим значенням та напрямком, називається векторної або вектором .

(Переміщення, сила, швидкість і т.д.)

Позначення: , або , .

Геометричний вектор – це спрямований відрізок.

Для вектора – точка А- Початок, крапка У- Кінець вектора.

Визначення 3.Модуль вектор – це довжина відрізка AB.

Визначення 4.Вектор, модуль якого дорівнює нулю, називається нульовим , позначається.

Визначення 5.Вектори, розташовані на паралельних прямих або на одній прямій називаються колінеарними . Якщо два колінеарні вектори мають однаковий напрямок, то вони називаються співспрямованими .

Визначення 6.Два вектори вважаються рівними , якщо вони співспрямовані та рівні за модулем.

Події над векторами.

1) Додавання векторів.

Опр. 6.Сумою двох векторів і є діагональ паралелограма, побудованого на цих векторах, що виходить із загальної точки їх застосування (Правило паралелограма).

Рис.1.

Опр. 7.Сумой трьох векторів , , називається діагональ паралелепіпеда, побудованого на цих векторах (Правило паралелепіпеда).

Опр. 8.Якщо А, У, З - довільні точки, то + = (Правило трикутника).

рис.2

Властивості додавання.

1 про . + = + (переміщувальний закон).

2 про . + (+) = (+) + = (+) + (сполучний закон).

3 про . + (– ) + .

2) Віднімання векторів.

Опр. 9.Під різницею векторів і розуміють вектор = – такий, що + = .

У паралелограмі – це інша діагональЦД (див. рис.1).

3) Розмноження вектора на число.

Опр. 10. Твором вектор на скаляр k називається вектор

= k = k ,

має довжину ka , та напрям, якого:

1. збігається з напрямом вектора, якщо k > 0;

2. протилежно напрямку вектора, якщо k < 0;

3. довільно, якщо k = 0.

Властивості множення вектора на число.

1 про . (k + l ) = k + l .

k ( + ) = k + k .

2 o . k (l ) = (kl ) .

3 o . 1  = , (–1)  = – , 0  = .

Властивості векторів.

Опр. 11.Два вектори і називаються колінеарними якщо вони розташовані на паралельних прямихабо на однієї прямої.

Нульовий вектор колінеарен будь-якому вектору.

Теорема 1.Два ненульові вектори та колінеарні,  коли вони пропорційні тобто.

= k , k - Скаляр.

Опр. 12.Три вектори , , називаються компланарними якщо вони паралельні деякій площині або лежать у ній.

Теорема 2.Три ненульові вектори , , компланарні,  коли один із них є лінійною комбінацією двох інших, тобто.

= k + l , k , l - Скаляри.

Вектор проекції на вісь.

Теорема 3.Проекція вектора на вісь (пряма спрямована) lдорівнює добутку довжини вектора на косинус кута між напрямком вектора та напрямком осі, тобто. = a  c os  ,  = ( , l).

2. КООРДИНАТИ ВЕКТОРА

Опр. 13.Проекції вектора на координатні осі Ох, Оу, Оzназиваються координати вектора. Позначення:  a x , a y , a z .

Довжина вектора:

Приклад:Обчислити довжину вектора.

Рішення:

Відстань між точками і обчислюється за такою формулою: .

Приклад:Знайти відстань між точками М (2,3,-1) та К (4,5,2).

Дії над векторами у координатній формі.

Дано вектори = a x , a y , a z і = b x , b y , b z .

1. (  )= a x  b x , a y  b y , a z  b z .

2.  =   a x ,  a y ,  a z, де  - Скаляр.

Скалярський витвір векторів.

Визначення:Під скалярним твором двох векторів та

розуміється число, рівне добутку довжин цих векторів на косинус кута з-поміж них, тобто. = , - Кут між векторами і .

Властивості скалярного твору:

1.  =

2. ( + ) =

3.

4.

5. де - скаляри.

6. два вектори перпендикулярні (ортогональні), якщо .

7. тоді і лише тоді, коли .

Скалярний твір у координатній формі має вигляд: , де і .

Приклад:Знайти скалярний твір векторів та

Рішення:

Вектор проведення векторів.

Визначення: Під векторним твором двох векторів і розуміється вектор, для якого:

Модуль дорівнює площі паралелограма, побудованого даних векторах, тобто. , де кут між векторами та

Цей вектор перпендикулярний векторам, що перемножуються, тобто.

Якщо вектори неколлінеарні, вони утворюють праву трійку векторів.

Властивості векторного твору:

1.При зміні порядку співмножників векторний твір змінює свій знак зворотний, зберігаючи модуль, тобто.

2 .Векторний квадрат дорівнює нуль-вектору, тобто.

3 .Скалярний множник можна виносити за символ векторного твори, тобто.

4 .Для будь-яких трьох векторів справедлива рівність

5 . Необхідна і достатня умова колінеарності двох векторів і:

Векторний твір у координатній формі.

Якщо відомі координати векторів та , то їхній векторний твір знаходиться за формулою:

.

Тоді з визначення векторного твору випливає, що площа паралелограма, побудованого на векторах і обчислюється за формулою:

Приклад:Обчислити площу трикутника з вершинами (1; -1; 2), (5; -6; 2), (1; 3; -1).

Рішення: .

Тоді площа трикутника АВС обчислюватиметься так:

,

Змішане твір векторів.

Визначення:Змішаним (векторно-скалярним) добутком векторів називається число, яке визначається за формулою: .

Властивості змішаного твору:

1. Змішане твір не змінюється за циклічної перестановки його співмножників, тобто. .

2. При перестановці двох сусідніх співмножників змішане твір змінює свій знак протилежний, тобто. .

3 .Необхідна та достатня умова компланарності трьох векторів. : =0.

4 .Змішане твір трьох векторів дорівнює обсягу паралелепіпеда, побудованого цих векторах, взятому зі знаком плюс, якщо ці вектори утворюють праву трійку, і зі знаком мінус, якщо вони утворюють ліву трійку, тобто. .

Якщо відомі координативекторів , той змішаний твір знаходиться за формулою:

Приклад:Обчислити змішане твір векторів.

Рішення:

3. Базис системи векторів.

Визначення.Під системою векторів розуміють кілька векторів, що належать одному і тому ж простору R.

Зауваження.Якщо система складається з кінцевого числа векторів, їх позначають однією і тією ж літерою з різними індексами.

приклад.

Визначення. Будь-який вид вектора = називається лінійною комбінацією векторів. Числа – коефіцієнтами лінійної комбінації.

приклад. .

Визначення. Якщо вектор є лінійною комбінацією векторів , то кажуть, що вектор лінійно виражається через вектори .

Визначення.Система векторів називається лінійно-незалежної, якщо жоден вектор системи не може бути лінійною комбінацією інших векторів. В іншому випадку систему називають лінійно-залежною.

приклад. Система векторів лінійно-залежна, тому що вектор .

Визначення базису.Система векторів утворює базис, якщо:

1) вона лінійно-незалежна,

2) будь-який вектор простору через неї лінійно виражається.

приклад 1.Базис простору: .

2. У системі векторів базисом є вектори: , т.к. лінійно виражається через вектори.

Зауваження.Щоб знайти базис даної системи векторів необхідно:

1) записати координати векторів у матрицю,

2) за допомогою елементарних перетворень привести матрицю до трикутного вигляду,

3) ненульові рядки матриці будуть базисом системи,

4) кількість векторів у базисі дорівнює рангу матриці.

Будуть і завдання для самостійного рішення, до яких можна переглянути відповіді.

Концепція вектор

Перш ніж Ви дізнаєтеся все про вектори та операції над ними, налаштуйтеся на вирішення нескладного завдання. Є вектор вашої підприємливості та вектор ваших інноваційних здібностей. Вектор підприємливості веде Вас до Цілі 1, а вектор інноваційних здібностей - до Цілі 2. Правила гри такі, що Ви не можете рухатися відразу за напрямками цих двох векторів і досягти відразу двох цілей. Вектори взаємодіють, або якщо говорити математичною мовою, над векторами проводиться деяка операція. Результатом цієї операції стає вектор "Результат", який наводить Вас до Цілі 3.

А тепер скажіть: результатом якої операції над векторами "Підприємливість" та "Інноваційні здібності" є вектор "Результат"? Якщо не можете сказати одразу, не сумуйте. У міру вивчення цього уроку Ви зможете відповісти на це запитання.

Як ми вже побачили вище, вектор обов'язково йде від певної точки Aпо прямій до деякої точки B. Отже, кожен вектор має як числове значення - довжину, але й фізичне і геометричне - спрямованість. З цього виводиться перше, найпростіше визначення вектора. Отже, вектор - це спрямований відрізок, що йде від точки Aдо точки B. Позначається він так: .

А щоб приступити до різних операціям із векторами нам потрібно познайомитися з ще одним визначенням вектора.

Вектор - це вид уявлення точки, до якої потрібно дістатися з деякої початкової точки. Наприклад, тривимірний вектор, як правило, записується у вигляді (х, y, z) . Говорячи дуже просто, ці числа означають, як далеко потрібно пройти в трьох різних напрямках, щоб дістатися точки.

Нехай дано вектор. При цьому x = 3 (права рука вказує праворуч), y = 1 (ліва рука вказує вперед), z = 5 (Під точкою стоїть сходи, що ведуть вгору). За цими даними ви знайдете точку, проходячи 3 метри в напрямку, що вказується правою рукою, потім 1 метр в напрямку, що вказується лівою рукою, а далі на Вас чекає сходи і, піднімаючись на 5 метрів, Ви, нарешті, опинитеся в кінцевій точці.

Решта термінів - це уточнення представленого вище пояснення, необхідні різних операцій над векторами, тобто, вирішення практичних завдань. Пройдемося цим суворішим визначенням, зупиняючись на типових завданнях на вектори.

Фізичними прикладамивекторних величин можуть бути зміщення матеріальної точки, що рухається в просторі, швидкість і прискорення цієї точки, а також сила, що діє на неї.

Геометричний векторпредставлений у двовимірному та тривимірному просторі у вигляді спрямованого відрізка. Це відрізок, у якого розрізняють початок та кінець.

Якщо A- Початок вектора, а B- його кінець, то вектор позначається символом або однією малою літерою. На малюнку кінець вектора вказується стрілкою (рис. 1)

Довжиною(або модулем) геометричного вектора називається довжина його відрізка, що породжує

Два вектори називаються рівними , якщо можуть бути поєднані (при збігу напрямів) шляхом паралельного переносу, тобто. якщо вони паралельні, направлені в ту саму сторону і мають рівні довжини.

У фізиці часто розглядаються закріплені вектори, задані точкою програми, довжиною та напрямком. Якщо точка програми вектора не має значення, то її можна переносити, зберігаючи довжину та напрямок у будь-яку точку простору. В цьому випадку вектор називається вільним. Ми домовимося розглядати лише вільні вектори.

Лінійні операції над геометричними векторами

Розмноження вектора на число

Добутком вектора на числоназивається вектор, що виходить з вектора розтягуванням (при ) або стисненням (при ) в раз, причому напрямок вектора зберігається, якщо , і змінюється на протилежне, якщо . (Мал. 2)

З визначення випливає, що вектори = завжди розташовані на одній або на паралельних прямих. Такі вектори називаються колінеарними. (Можна говорити також, що ці вектори паралельні, проте у векторній алгебрі прийнято говорити "колінеарні".) Справедливо і зворотне твердження: якщо вектори і колінеарні, то вони пов'язані ставленням

Отже, рівність (1) висловлює умову колінеарності двох векторів.

Складання та віднімання векторів

При складанні векторів потрібно знати, що сумоювекторів і називається вектор , початок якого збігається з початком вектора , а кінець - з кінцем вектора , за умови, що початок вектора прикладено до кінця вектора . (Мал. 3)

Це визначення може бути розподілене на будь-яке кінцеве число векторів. Нехай у просторі дані nвільних векторів. При додаванні кількох векторів їх суму приймають замикаючий вектор, початок якого збігається з початком першого вектора, а кінець - з кінцем останнього вектора. Тобто, якщо до кінця вектора додати початок вектора, а до кінця вектора - початок вектора і т.д. і, нарешті, до кінця вектора - початок вектора , то сумою цих векторів служить замикаючий вектор початок якого збігається з початком першого вектора, а кінець - з кінцем останнього вектора. (Мал. 4)

Доданки називаються складовими вектора, а сформульоване правило - правилом багатокутника. Цей багатокутник може бути плоским.

При множенні вектора число -1 виходить протилежний вектор . Вектори мають однакові довжини і протилежні напрямки. Їхня сума дає нульовий вектор, Довжина якого дорівнює нулю. Напрямок нульового вектора не визначено.

У векторной алгебрі немає необхідності розглядати окремо операцію віднімання: відняти з вектора вектор означає додати до вектора протилежний вектор, тобто.

приклад 1.Спростити вираз:

.

,

тобто, вектори можна складати і множити числа так само, як і багаточлени (зокрема, також завдання на спрощення виразів). Зазвичай, необхідність спрощувати лінійно подібні вирази з векторами виникає перед обчисленням творів векторів.

приклад 2.Вектори і є діагоналями паралелограма ABCD (рис. 4а). Виразити через вектори , , і , що є сторонами цього паралелограма.

Рішення. Точка перетину діагоналей паралелограма поділяє кожну діагональ навпіл. Довжини необхідних умов завдання векторів знаходимо або як половини сум векторів, що утворюють з шуканими трикутник, або як половини різниць (залежно від напрямку вектора, що служить діагоналлю), або, як в останньому випадку, половини суми, взятої зі знаком мінус. Результат - необхідні завдання вектори:

Є всі підстави вважати, що тепер Ви правильно відповіли на запитання про вектори "Підприємливість" та "Інноваційні здібності" на початку цього уроку. Правильна відповідь: над цими векторами провадиться операція складання.

Вирішити завдання на вектори самостійно, а потім переглянути рішення

Як знайти довжину суми векторів?

Це завдання займає особливе місце в операціях з векторами, оскільки передбачає використання тригонометричних властивостей. Допустимо, Вам трапилося завдання на кшталт наступного:

Дані довжини векторів та довжина суми цих векторів. Знайти довжину різниці цих векторів.

Рішення цієї та інших подібних завданьі пояснення, як їх вирішувати - на уроці " Додавання векторів: довжина суми векторів і теорема косінусів. ".

А перевірити вирішення таких завдань можна на Калькулятор онлайн "Невідома сторона трикутника (складання векторів і теорема косінусів)" .

А де твори векторів?

Твори вектора вектор не є лінійними операціями і розглядаються окремо. І у нас є уроки "Скалярний твір векторів" та "Векторний та змішаний твор векторів".

Вектор проекції на вісь

Проекція вектора на вісь дорівнює добутку довжини вектора, що проектується, на косинус кута між вектором і віссю:

Як відомо, проекцією точки Aна пряму (площину) служить основу перпендикуляра, опущеного з цієї точки на пряму (площину).

Нехай – довільний вектор (Рис. 5), а й – проекції його початку (точки A) та кінця (точки B) на вісь l. (Для побудови проекції точки A) на пряму проводимо через точку Aплощину, перпендикулярну до прямої. Перетин прямої та площини визначить необхідну проекцію.

Складає вектор на осі lназивається такий вектор, що лежить на цій осі, початок якого збігається з проекцією початку, а кінець - з проекцією кінця вектора.

Вектор проекції на вісь lназивається число

,

рівне довжині складового вектора на цій осі, взяте зі знаком плюс, якщо напрямок складової збігається з напрямком осі lі зі знаком мінус, якщо ці напрямки протилежні.

Основні властивості проекцій вектора на вісь:

1. Проекції рівних векторів на ту саму вісь рівні між собою.

2. При множенні вектора на число його проекція множиться на це число.

3. Проекція суми векторів на якусь вісь дорівнює сумі проекцій на цю вісь доданків векторів.

4. Проекція вектора на вісь дорівнює добутку довжини проектованого вектора на косинус кута між вектором і віссю:

.

Рішення. Спроектуємо вектори на вісь lяк визначено у теоретичній довідці вище. З рис.5а очевидно, що проекція суми векторів дорівнює сумі векторних проекцій. Обчислюємо ці проекції:

Знаходимо остаточну проекцію суми векторів:

Зв'язок вектора з прямокутною декартовою системою координат у просторі

Знайомство з прямокутною декартовою системою координат у просторі відбулося у відповідному уроцібажано відкрити його в новому вікні.

Впорядкована система координатних осей 0xyzвісь Oxназивається віссю абсцисвісь 0y – віссю ординат, і вісь 0z – віссю аплікат.

З довільною точкою Мпростору зв'яжемо вектор

званий радіус-векторомкрапки Мта спроектуємо його на кожну з координатних осей. Позначимо величини відповідних проекцій:

Числа x, y, zназиваються координатами точки Мвідповідно абсцисою, ординатоюі аплікати, і записуються як упорядкованої точки чисел: M (x; y; z)(Рис.6).

Вектор одиничної довжини, напрямок якого збігається із напрямком осі, називають одиничним вектором(або ортом) Осі. Позначимо через

Відповідно орти координатних осей Ox, Ой, Oz

Теорема.Будь-який вектор може бути розкладений по орт координатних осей:

(2)

Рівність (2) називається розкладанням вектора за координатними осями. Коефіцієнтами цього розкладання є проекції вектора координатні осі. Таким чином, коефіцієнтами розкладання (2) вектора координатними осями є координати вектора.

Після вибору в просторі певної системи координат вектор і трійка координат однозначно визначають один одного, тому вектор може бути записаний у формі

Подання вектора як (2) і (3) тотожні.

Умова колінеарності векторів у координатах

Як ми вже зазначали, вектори називаються колінеарними, якщо вони пов'язані ставленням

Нехай дані вектори . Ці вектори є колінеарними, якщо координати векторів пов'язані ставленням

,

тобто, координати векторів пропорційні.

Приклад 6.Дано вектори . Чи колінеарні ці вектори?

Рішення. З'ясуємо співвідношення координат даних векторів:

.

Координати векторів пропорційні, отже, вектори колінеарні, або, що те саме, паралельні.

Довжина вектора та напрямні косинуси

Внаслідок взаємної перпендикулярності координатних осей довжина вектора

дорівнює довжині діагоналі прямокутного паралелепіпеда, побудованого на векторах

і виражається рівністю

(4)

Вектор повністю визначається завданням двох точок (початку та кінця), тому координати вектора можна виразити через координати цих точок.

Нехай у заданій системі координат початок вектора знаходиться у точці

а кінець – у точці

З рівності

Випливає, що

або в координатній формі

Отже, координати вектора рівні різницям однойменних координат кінця та початку вектора . Формула (4) у цьому випадку набуде вигляду

Напрямок вектора визначають напрямні косинуси . Це косинуси кутів, які вектор утворює з осями. Ox, Ойі Oz. Позначимо ці кути відповідно α , β і γ . Тоді косинуси цих кутів можна знайти за формулами

Напрямні косинуси вектора є координатами орта цього вектора і, таким чином, орт вектора

.

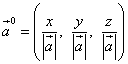
Враховуючи, що довжина векторного орта дорівнює одній одиниці, тобто

,

отримуємо наступну рівність для напрямних косінусів:

Приклад 7.Знайти довжину вектора x = (3; 0; 4).

Рішення. Довжина вектора дорівнює

Приклад 8.Дані точки:

З'ясувати, чи рівнобедрений трикутник, побудований на цих точках.

Рішення. За формулою довжини вектора (6) знайдемо довжини сторін і встановимо, чи є серед них дві рівні:

Дві рівні сторони знайшлися, тому необхідність шукати довжину третьої сторони відпадає, а заданий трикутник є рівнобедреним.

Приклад 9.Знайти довжину вектора та його напрямні косинуси, якщо .

Рішення. Координати вектора:

.

Довжина вектора дорівнює квадратного кореняіз суми квадратів координат вектора:

.

Знаходимо напрямні косинуси:

Вирішити завдання на вектори самостійно, а потім переглянути рішення

Операції над векторами, заданими у координатній формі

Нехай дані два вектори і , задані своїми проекціями:

Вкажемо події над цими векторами.

Дата створення: 2009-04-11 15:25:51
Останній раз внесено зміни: 2012-02-08 09:19:45

Довго я не хотів писати цю статтю – думав як подавати матеріал. Ще й малюнки треба малювати. Проте, мабуть сьогодні успішно склалися зірки і статті про вектори бути. Хоча, це лише чорновий варіант. У майбутньому цю статтю розіб'ю на кілька окремих - матеріалу достатньо. Також, поступово стаття покращуватиметься: вноситиму до неї зміни - т.к. за один раз не вдасться розкрити всі аспекти.

Вектори були введені в математику в XIX столітті, для опису величин, які важко було описувати за допомогою скалярних значень.

Вектори інтенсивно застосовуються розробки комп'ютерних ігор. Застосовуються вони як традиційно - для описи таких величин як сила чи швидкість, а й у областях, які здавалося б не пов'язані з векторами: зберігання кольору, створення тіней.

Скаляри та вектори

Спочатку нагадаю, що таке скаляр, і чим він відрізняється від вектора.

Скалярні значення зберігають якусь величину: маса, об'єм. Тобто це сутність, яка характеризується лише одним числом (наприклад, кількість чогось).

Вектор на відміну від скаляра описується за допомогою двох значень: величина та напрямок.

Важлива відмінність векторів від координат: вектори не прив'язані до конкретного розташування! Ще раз повторюся, головне у векторі – довжина та напрямок.

Вектор позначається жирною літерою латинського алфавіту. Наприклад: a, b, v.

На першому малюнку можна побачити, як вектор позначають на площині.

Вектори в просторі

У просторі вектори можна виражати за допомогою координат. Але насамперед потрібно запровадити одне поняття:

Радіус-вектор точки

Візьмемо у просторі якусь точку M(2,1). Радіус-вектор точки - це вектор, що починається на початку координат і закінчується в точці.

У нас тут ні що інше як вектор OM. Координати початку вектора (0,0), координати кінця (2,1). Позначимо цей вектор як a.

В даному випадку вектор можна записати в такий спосіб a = <2, 1>. Це координатна форма вектора a.

Координати вектора називаються його компонентами щодо осей. Наприклад, 2 - компонета вектора aщодо осі x.

Давайте знову зупинимося на тому, що таке координати точки. Координата точки (наприклад x) – це проекція точки на вісь, тобто. основу перпендикуляра, опущеного з точки на вісь. У прикладі 2.

Але повернемося до першого малюнку. У нас тут дві точки A та B. Нехай координатами точок будуть (1,1) та (3,3). Вектор vу разі можна позначити так v = <3-1, 3-1>. Вектор тривимірного простору, що лежить у двох точках, буде виглядати так:

v =

Думаю жодних складнощів тут немає.

Розмноження вектора на скаляр

Вектор можна множити на скалярні значення:

k v = =

У цьому скалярне значення перемножується з кожною компонентою вектора.

Якщо k > 1, вектор збільшиться, якщо k менше одиниці, але більше нуля - вектор зменшиться в довжину. Якщо ж k менше нуля, то вектор змінить напрямок.

Поодинокі вектори

Поодинокі вектори - це вектори довжина яких дорівнює одиниці. Зауважте, вектор з координатами<1,1,1>не буде рівним одиниці! Знаходження довжини вектора наведено нижче за текстом.

Існують так звані орти – це поодинокі вектори, які за напрямом збігаються з осями координат. i- орт осі x, j- орт осі y, k- Орт осі z.

При цьому i = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

Тепер ми знаємо, що таке множення вектора на скаляр і що таке поодинокі вектори. Тепер ми можемо записати vу векторному вигляді.

v= v x i+ v y j+ v z k, де v x , v y , v z - відповідні компоненти вектора

Складання векторів

Щоб повністю розібратися в попередній формулі, необхідно зрозуміти, як працює складання векторів.

Тут все просто. Візьмемо два вектори v1 = та v 2 =

v 1 + v 2 =

Ми лише складаємо відповідні компоненти двох векторів.

Різниця обчислюється так само.

Це стосується математичної форми. Для повноти, варто розглянути як виглядатиме додавання та віднімання векторів графічно.

Для того, щоб скласти два вектори a+b. Потрібно поєднати початок вектору bта кінець вектора a. Потім, між початком вектора aта кінцем вектора bпровести новий вектор. Для наочності дивіться другий малюнок (літера "а").

Для віднімання векторів потрібно поєднати початку двох векторів і провести новий вектор із кінця другого вектора до кінця першого. На другому малюнку (літера "б") показано, як воно виглядає.

Довжина та напрямок вектора

Спочатку розглянемо довжину.

Довжина - це числове значення вектора, без урахування напряму.

Довжина визначається за формулою (для тривимірного вектора):

корінь квадратний із суми квадратів компонент вектор.

Знайома формула, чи не так? Загалом це формула довжини відрізка

Напрямок вектора визначається напрямними косинусами кутів утворених між вектором і осями координат. Для знаходження напрямних косінусів використовуються відповідні компоненти та довжина (картинка буде пізніше).

Подання векторів у програмах

Представляти вектори в програмах можна у різний спосіб. Як за допомогою звичайних змінних, що не ефективно, так і за допомогою масивів, класів та структур.

Float vector3 = (1,2,3); // масив зберігання вектора struct vector3 // структура зберігання векторів ( float x,y,z; );

Найбільші можливості для зберігання векторів нам надають класи. У класах ми можемо описати як сам вектор (змінні), а й векторні операції (функції).

Скалярний добуток векторів

Існує два типи перемноження векторів: векторне та скалярне.

Відмінна риса скалярного твори - у результаті завжди буде скалярне значення, тобто. число.

Тут варто звернути увагу на якийсь момент. Якщо результат цієї операції дорівнює нулю, отже, два вектори перпендикулярні – кут між ними 90 градусів. Якщо результат більший за нуль - кут менше 90 градусів. Якщо результат менший за нуль, кут більше 90 градусів.

Цю операцію представляє така формула:

a · b= a x * b x + a y * b y + a z * b z

Скалярне твір - це сума творів відповідних компонентів двох векторів. Тобто. Беремо x"и двох векторів, перемножуємо їх, потім складаємо з твором y"ів і так далі.

Векторний твір векторів

Результатом векторного добутку двох векторів буде перпендикулярний вектор векторам.

a x b =

Ми поки що не обговорюватимемо докладно цю формулу. До того ж, вона досить важка для запам'ятовування. Ми повернемося до цього моменту після знайомства з визначниками.

Ну і для загального розвитку корисно знати, що довжина отриманого вектора дорівнює площі паралелограма побудованого на векторах aі b.

Нормалізація вектора

Нормалізований вектор - це вектор, довжина якого дорівнює одиниці.

Формула для знаходження нормалізованого вектора наступна – всі компоненти вектора необхідно розділити на його довжину:

v n = v/ | V | =

Післямова

Як ви, мабуть, переконалися, вектори не складні для розуміння. Ми розглянули низку операцій над векторами.

У наступних статтях розділу "математика" ми обговорюватимемо матриці, визначники, системи лінійних рівнянь. Це все теорія.

Після цього ми розглянемо перетворення матриць. Саме тоді Ви зрозумієте, наскільки важлива математика у створенні комп'ютерних ігор. Ця тема якраз і стане практикою з усіх попередніх тем.