Головна фізика Творча робота "застосування формули піку". геометрія

Творча робота "застосування формули піку". геометрія

Формула Піка

1. Введення

2. Формула Піка. Доказ I.

Доказ II.

Доказ Ш.

3. Завдання.

4. Формула площі багатокутника через координати вершин.

5. Завдання.

6. Література

Формула Піка.

1. Введення.

В історії черпаємо ми мудрість,

в поезії - дотепність,

в математиці - проникливість.

Ф. Бекон

Сюжет розгортатиметься на звичайному листку картатій паперу.

Лінії, що йдуть по сторонам клітин, утворюють сітку, а вершини клітин - вузли цієї сітки. Намалюємо на аркуші багатокутник з вершинами у вузлах і знайдемо його площу.

Шукати її можна по - різному. Наприклад, можна розрізати багатокутник на досить прості фігури, знайти їх площі і скласти.

Але тут нас чекає багато клопоту. Фігура легко розбивається на прямокутники, трапеції, і трикутники, і її площа обчислюється без зусиль.

Хоча багатокутник і виглядає досить просто, для обчислення його площі доведеться неабияк потрудитися. А якби багатокутник виглядав більш химерно? Виявляється, площі багатокутників, вершини яких розташовані в вузлах сітки, можна обчислювати набагато простіше: є формула, що зв'язує їх площа з кількістю вузлів, що лежать всередині і на кордоні багатокутника. Ця чудова і проста формула називається формулою Піка.

2. Формула Піка.

Вершини багатокутника (не обов'язково опуклого) розташовані в вузлах целочисленной решітки. Всередині його лежить В вузлів решітки, а на кордоні Г вузлів. Доведемо, що його площа дорівнює В + - 1 (формула Піка).

Доказ I.

Розглянемо багатокутник, вершини якого знаходяться в вузлах целочисленной решітки, тобто мають цілочисельні координати.

Багатокутник розіб'ємо на трикутники з вершинами у вузлах решітки, що не містять вузлів ні всередині, ні на сторонах.

позначимо:

n - число сторін багатокутника,

m - кількість трикутників з вершинами у вузлах решітки, що не містять вузлів ні всередині, ні на сторонах,

В - число вузлів всередині багатокутника,

Г - число вузлів на сторонах, включаючи вершини.

Площі всіх цих трикутників однакові і рівні.

Отже, площа багатокутника дорівнює
.

180 0 m .

Тепер знайдемо цю суму іншим способом.

Сума кутів з вершиною в будь-якому внутрішньому вузлі становить 360 0.

Тоді сума кутів з вершинами у всіх внутрішніх вузлах дорівнює 360 0 В.

Загальна сума кутів при вузлах на сторонах, але не в вершинах дорівнює 180 0 (Г - n).

Сума кутів при вершинах багатокутника дорівнює 180 0 ( n – 2) .

Загальна сума кутів всіх трикутників дорівнює 360 0 В + 180 0 (Г - n) + 180 0 (n – 2).

Таким чином, 180 0 m \u003d 360 0 В + 180 0 (Г - n) + 180 0 (n – 2),

180 0 m \u003d 360 0 В + 180 0 Г - 180 0 n + 180 0 n - 180 0 · 2,

180 0 m \u003d 360 0 В + 180 0 Г- 360 0,

\u003d В + – 1 ,

звідки отримуємо вираз для площі S багатокутника:

S\u003d В + – 1 ,

відоме як формула Піка.

На малюнку: В \u003d 24, Г \u003d 9, отже,S = 24 + – 1 = 27,5.

Знайдемо площу першого багатокутника за формулою Піка:

В \u003d 28 (зелені крапки);

Г \u003d 20 (сині точки).

Отримуємо, S \u003d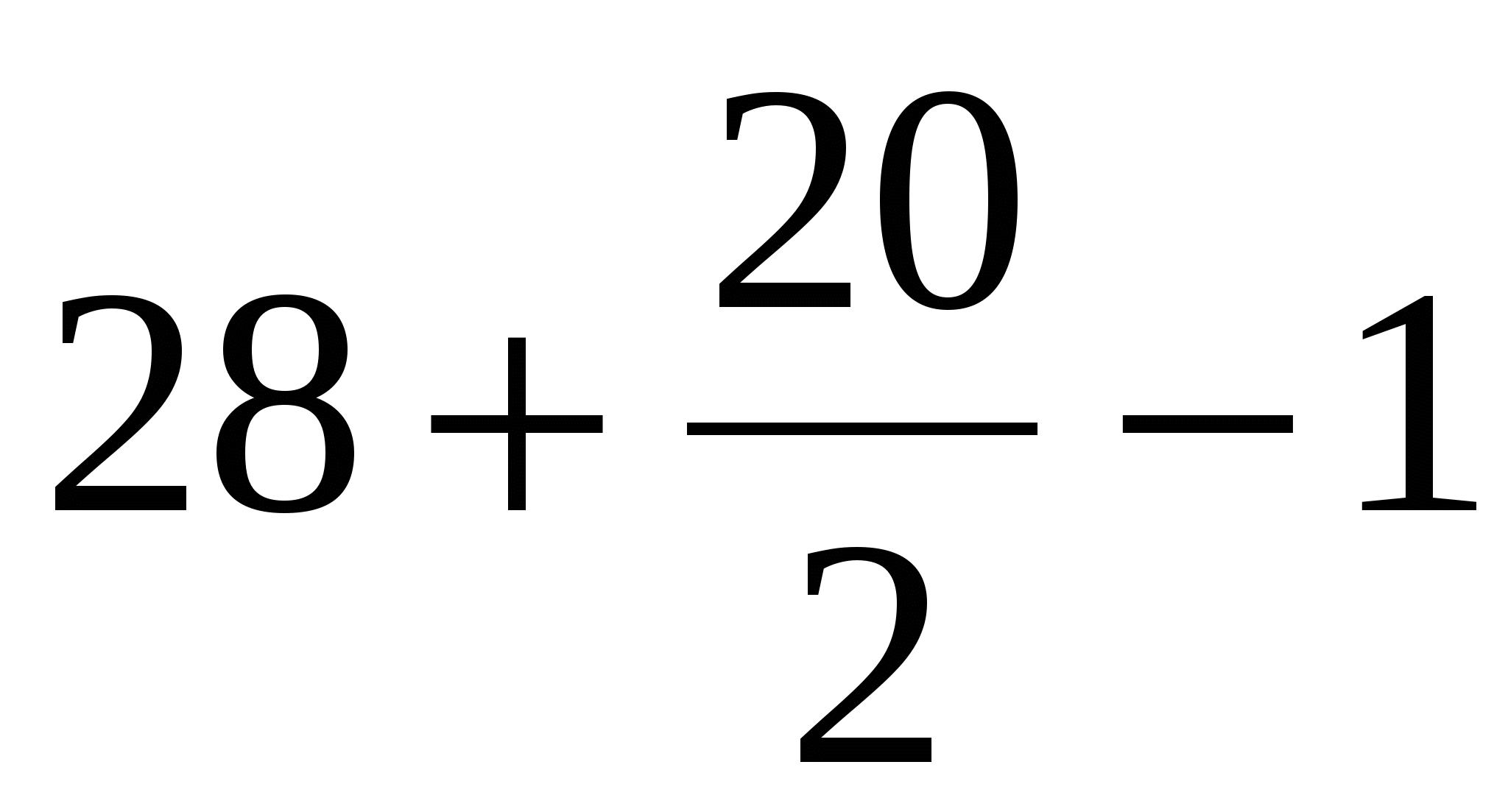
\u003d 37 кв.ед.

Доказ II.

Кожному многоугольнику M з вершинами у вузлах целочисленной решітки поставимо у відповідність число f (M) \u003d
, Де підсумовування ведеться по всіх вузлах решітки, що належить M, а кут визначається наступним чином: =
для внутрішньої точки багатокутника, =
для граничної точки, відмінною від вершини, і - кут при вершині, якщо даний вузол - вершина. Легко бачити, що f (M) \u003d
+
\u003d В + - 1. Залишається перевірити, що число f (M) дорівнює площі багатокутника M.

Нехай багатокутник M розрізаний на багатокутники M 1 і M 2 з вершинами у вузлах решітки. Тоді f (M) \u003d f (M 1) + f (M 2), оскільки для кожного вузла кути складаються. Тому якщо формула Піка вірна для двох з багатокутників M, M 1 і M 2, то вона вірна і для третього.

Якщо M - прямокутник зі сторонами p і q, Спрямованими по лініях решітки, то

f (M) \u003d (p - 1) (q - 1) +
\u003d Pq.

У цьому випадку формула Піка справедлива. Розрізавши прямокутник M діагоналлю на трикутники M 1 і M 2 і скориставшись тим, що f (M) \u003d f (M 1) + f (M 2) і f (M 1) \u003d f (M 2), легко довести справедливість формули Піка для будь-якого прямокутного трикутника з катетами, спрямованими по лініях решітки. Відрізавши кілька таких трикутників від прямокутника, можна отримати будь-який трикутник.

Для завершення докази формули Піка залишається зауважити, що будь-який багатокутник можна розрізати на трикутники непересічними діагоналями.

Доказ Ш.

Зв'язок між площею фігури і кількістю вузлів, що потрапили в цю фігуру, особливо ясно видно в разі прямокутника.

нехай ABCD - прямокутник з вершинами у вузлах і сторонами, що йдуть по лініях сітки.

позначимо через Вкількість вузлів, що лежать всередині прямокутника, а через Г - кількість вузлів на його кордоні. Змістимо сітку на підлогу клітки вправо і полклеткі вниз.

Тоді територію прямокутника можна «розподілити» між вузлами в такий спосіб: кожен з Ввузлів «контролює» цілу клітку зміщеною сітки, кожен з Г - 4 граничних некутових вузла - половину клітини, а кожна з кутових точок - чверть клітини. Тому площа прямокутника S дорівнює

Отже, для прямокутників з вершинами у вузлах і сторонами, що йдуть по лініях сітки, ми встановили формулу

Доведемо, що ця формула вірна не тільки для прямокутників, а й для довільних багатокутників з вершинами у вузлах сітки.

позначимо через S м площа багатокутникаМ з вершинами у вузлах, а черезП м - величину
, деВ м - число вузлів всерединіМ, а Г м - число вузлів на кордоні. Тоді формулу Піка можна записати у вигляді
.

Доведення формули розіб'ємо на кілька кроків.

Крок 1.

якщо багатокутникМ з вершинами у вузлах сітки розрізаний на 2 багатокутникаМ 1 і М 2 , також мають вершини тільки в вузлах сітки, то
. нехай багатокутникМ розрізаний на багатокутникиМ 1 і М 2 з вершинами у вузлах відрізкомАВ. Всі вузли, крім тих, які потрапляють на відрізокАВ, дають однаковий внесок у ліву і праву частини формули. Розглянемо вузли, що лежать на відрізку АВ.

Якщо такий вузол лежить між А і В (наприклад, С), то для багатокутникаМ він внутрішній, а для багатокутниківМ 1 і М 2 - граничний. Тому його внесок вП м дорівнює 1, а в кожне з виразів
і
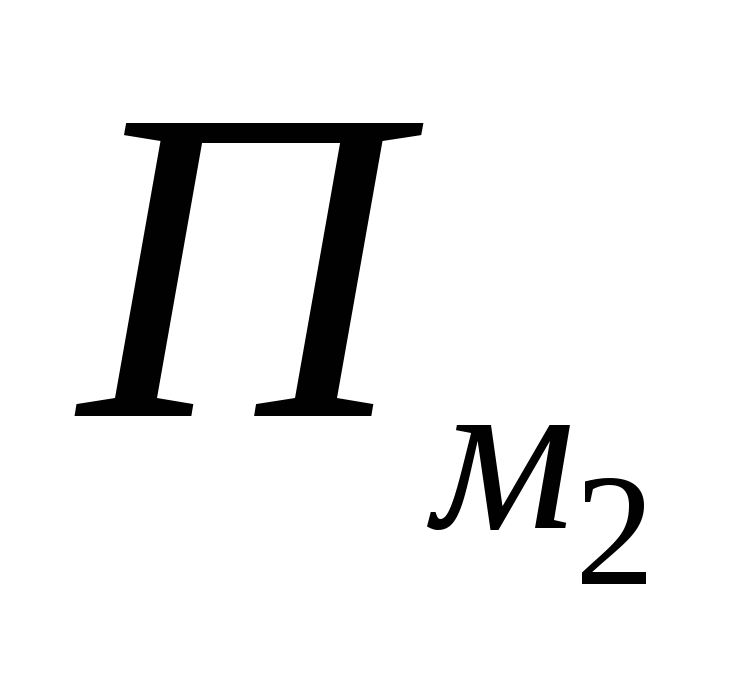- по 0,5, тобто вклади такого вузла вП м і
рівні.

Розглянемо вузли А і В. Вони граничні як для М, Так і для М 1 , М 2 .

Тому внесок кожного з цих вузлів вП м дорівнює 0,5 а в
- одиниці. Значить, сумарний внесок вузлів А і В уП м дорівнює 1, що на 1 менше, ніж їх внесок в
. але
, А.

Із загальної «вкладу» всіх вузлів П м віднімається 1, а з
віднімається 2, і це компенсує різницю вкладів вузлів А і В.

Отже,
.

Крок 2.

якщо багатокутник Мз вершинами у вузлах сітки розрізаний на два багатокутника М 1 і М 2 (Теж з вершинами у вузлах) і формула вірна для якихось двох з багатокутників М, М 1 , М 2 , То вона вірна і для третього багатокутника.

Нехай, наприклад, вона вірна дляМ 1 і М 2 , тобто
. Тоді (за першого кроку), але по першого кроку) останній вираз одноП м , а рівність
і є формула Піка.

Крок 3.

Доведемо формулу Піка для прямокутного трикутника з вершинами у вузлах сітки і катетами, що лежать на лініях сітки.

трикутник АВС добудуємо до прямокутника ABCD .

Для прямокутників формула Піка вірна: S ABCD \u003d П ABCD . Відповідно до першого кроку П ABCD \u003d П ABC + П ACD , П ABC \u003d П ACD , так що П ABCD \u003d 2П ABC . але S ABCD = 2 S ABC . Тому S ABC \u003d П ABC .

Крок 4.

Формула Піка вірна для довільного трикутника з вершинами у вузлах сітки.

Розглянувши малюнок, легко зрозуміти: будь-який такий трикутник можна отримати, «відрізавши» від деякого прямокутника зі сторонами, що йдуть по лініях сітки, кілька прямокутників і прямокутних трикутників з катетами на лініях сітки. А так як формула Піка вірна для прямокутників і прямокутних трикутників, то (згадаємо крок 2) вона вірна і для вихідного трикутника.

Ми довели, що якщо багатокутник можна розрізати на трикутники з вершинами у вузлах сітки, то для нього вірна формула Піка.

3. Завдання.

Знайдіть площі фігур:

1
.

B \u003d 9

Г \u003d 4

B \u003d 9

Г \u003d 5

Гібадуллін Г.І. (Нурлат, МАОУ ЗОШ №1)

1. Бунимович Е.А., Дорофєєв Г.В., Суворова С.Б. та ін. Математика. Арифметика. Геометрія. 5 клас: навч. для загальноосвіт. організацій з дод. на електрон. носії -3-е изд. - М .: Просвещение, 2014. - 223, с. : Ил. - (Сфери).

2. Бунимович Е.А., Кузнєцова Л.В., Мінаєва С.С. та ін. Математика. Арифметика. Геометрія. 6 клас: навч. для загальноосвіт. організацій. 5-е изд. - М .: Просвещение, 2016. - 240 с .: іл. - (Сфери).

3. Васильєв Н.Б. Навколо формули Піка // Квант. - 1974. - №2. - С. 39-43.

4. Розсолів В.В. Завдання з планіметрії. 5-е изд., Испр. і доп. - М .: 2006. - 640 с.

5. Ященко І.В. ОГЕ. Математика: типові екзаменаційні варіанти: О-39 36 варіантів - М .: Изд-во «Національна освіта», 2017. - 240 с. - (ОГЕ. ФІПІ - школі).

6. Вирішу ОГЕ: математика. Навчальна система Дмитра Гущина. ОГЕ-2017: завдання, відповіді, рішення [Електронний ресурс]. - Режим доступу: https://oge.sdamgia.ru/test?id\u003d6846966 (дата звернення 02.04.2017).

Я учень 6 класу. Вивчати геометрію почав ще з минулого року, адже займаюся я в школі за підручником «Математика. Арифметика. Геометрія »під редакцією Е.А. Бунимович, Л.В. Кузнєцова, С.С. Мінаєва та інші.

Найбільше мою увагу привернули теми «Площі фігур», «Складання формул». Я помітив, що площі одних і тих самих фігур можна знаходити різними способами. У побуті ми часто стикаємося з завданнями знаходження площі. Наприклад, знайти площу підлоги, який доведеться пофарбувати. Цікаво адже, щоб купити необхідну кількість шпалер для ремонту, потрібно знати розміри кімнати, тобто площа стін. Обчислення площі квадрата, прямокутника і прямокутного трикутника не викликало у мене труднощів.

Зацікавившись цією темою, я почав шукати додатковий матеріал в Інтернеті. В результаті пошуків я натрапив на формулу Піка- це формула для обчислення площі багатокутника, намальованого на картатій папері. Обчислення площі за цією формулою мені здалося доступним будь-якому учневі. Саме тому я вирішив провести дослідницьку роботу.

Актуальність теми. Дана тема є доповненням і поглибленням вивчення курсу геометрії.

Вивчення даної теми допоможе краще підготуватися до олімпіад і іспитів.

Мета роботи:

1. Ознайомитися з формулою Піка.

2. Оволодіти прийомами рішень геометричних задач з використанням формули Піка.

3. Систематизувати і узагальнити теоретичний і практичний матеріали.

Завдання дослідження:

1. Перевірити ефективність і доцільність застосування формули при вирішенні завдань.

2. Навчитися застосовувати формулу Піка в задачах різної складності.

3. Порівняти завдання, вирішені за допомогою формули Піка і традиційним способом.

Основна частина

Історична довідка

Георг Олександр Пік - австрійський математик, народився 10 серпня року. Він був обдарованою дитиною, його навчав батько, який очолював приватний інститут. У 16 років Георг закінчив школу і вступив до Віденського університету. У 20 років отримав право викладати фізику і математику. Всесвітню популярність йому принесла формула для визначення площі решітки полігонів. Свою формулу він опублікував в статті в 1899 році. Вона стала популярною, коли польський вчений Хьюго Штейнгауз включив її в 1969 році в видання математичних знімків.

Георг Пік отримав освіту у Віденському університеті і захистив кандидатську в 1880 році. Після отримання докторського ступеня він був призначений помічником Ернеста Маха в Шерльско- Фердінандском університеті в Празі. Там же він став викладачем. Він залишався в Празі до своєї відставки в 1927 році, а потім повернувся до Відня.

Пік очолював комітет у німецькому університеті Праги, який призначив Ейнштейна професором кафедри математичної фізики в 1911 році.

Він був обраний членом Чеської академії наук і мистецтв, але був виключений після захоплення нацистами Праги.

Коли нацисти увійшли до Австрії 12 березня 1938 року він повернувся Прагу. У березні 1939 року нацисти вторглися в Чехословаччину. 13 липня 1942 року Пік був депортований в створений нацистами в північній Чехії табір Терезієнштадт, де помер через два тижні у віці 82 років.

Дослідження і доказ

Свою дослідницьку роботу я почав зі з'ясування питання: площі яких фігур я зможу знайти? Скласти формулу для обчислення площі різних трикутників і чотирикутників я міг. А як же бути з п'яти-, шести-, і взагалі з багатокутниками?

В ході дослідження на різних сайтах я побачив вирішення завдань на обчислення площі п'яти-, шести-, і інших багатокутників. Формула, що дозволяє вирішувати ці завдання, називалася формулою Піка. Вона виглядає так: S \u003d B + Г / 2-1, де В - кількість вузлів, що лежать всередині багатокутника, Г - кількість вузлів, що лежать на кордоні багатокутника. Особливість цієї формули полягає в тому, що її можна застосовувати тільки для багатокутників, намальованих на картатій папері.

Будь-який такий багатокутник легко розбити на трикутники з вершинами у вузлах решітки, що не містять вузлів ні всередині, ні на сторонах. Можна показати, що площі всіх цих трикутників однакові і рівні ½, а отже, площа багатокутника дорівнює половині їх числа Т.

Щоб знайти це число, позначимо через n число сторін багатокутника, через В - число вузлів всередині нього, через Г - число вузлів на сторонах, включаючи вершини. Загальна сума кутів всіх трикутників дорівнює 180 °. Т.

Тепер знайдемо суму іншим способом.

Сума кутів з вершиною в будь-якому внутрішньому вузлі становить 2.180 °, тобто загальна сума кутів дорівнює 360 °. В; загальна сума кутів при вузлах на сторонах, але не в вершинах дорівнює (Г - n) 180 °, а сума кутів при вершинах багатокутника буде дорівнює (Г - 2) 180 °. Таким чином, Т \u003d 2.180 °. В + (Г-n) 180 ° + (n-2) 180 °. Виконавши розкриття дужок і розділивши на 360 °, отримуємо формулу для площі S багатокутника, відому як формула Піка.

Практична частина

Цю формулу вирішив перевірити на завданнях зі збірки ОГЕ-2017. Взяв завдання на обчислення площі трикутника, чотирикутника і п'ятикутника. Вирішив порівняти відповіді, вирішуючи двома способами: 1) доповнив фігури до прямокутника і з площі отриманого прямокутника вирахував площа прямокутних трикутників; 2) застосував формулу Піка.

S \u003d 18-1,5-4,5 \u003d 12 і S \u003d 7 + 12 / 2-1 \u003d 12.

S \u003d 24-9-3 \u003d 12 і S \u003d 7 + 12 / 2-1 \u003d 12.

S \u003d 77-7,5-12-4,5-4 \u003d 49 і S \u003d 43 + 14 / 2-1 \u003d 49.

Порівнявши отримане, роблю висновок, що обидві формули дають один і той же відповідь. Знайти площу фігури за формулою Піка, виявилося швидше і легше, адже обчислень було менше. Легкість рішення і економія часу на обчисленнях мені знадобляться в майбутньому при здачі ОГЕ.

Це підштовхнуло мене на перевірку можливості застосування формули Піка на більш складних фігурах.

S \u003d 0 + 4/2 -1 \u003d 1

S \u003d 5 + 11 / 2-1 \u003d 9,5

S \u003d 4 + 16 / 2-1 \u003d 1

висновок

Формула Піка проста в розумінні і зручна в застосуванні. По-перше, достатньо вміти рахувати, ділити на 2, додавати і віднімати. По-друге, можна знайти площу і складної фігури, не витративши багато часу. По-третє, ця формула працює для будь-якого багатокутника.

Недолік у тому, що Формула Піка застосовна тільки для фігур, які намальовані на картатій папері і вершини лежать на вузлах клітин.

Я впевнений, що при здачі випускних іспитів, завдання на обчислення площі фігур не викликатимуть труднощі. Адже я вже знайомий з формулою Піка.

бібліографічна посилання

Габбазов М.М. ФОРМУЛА ПІКу // Старт в науці. - 2017. - № 6-1. - С. 130-132;
URL: http://science-start.ru/ru/article/view?id\u003d908 (дата звернення: 05.03.2020).

Текст роботи розміщений без зображень і формул.
Повна версія роботи доступна у вкладці "Файли роботи" в форматі PDF

Вступ

Я, учень 6 класу. Вивчати геометрію почав ще з минулого року, адже займаюся я в школі за підручником «Математика. Арифметика. Геометрія »під редакцією Е.А. Бунимович, Л.В.Кузнецова, С.С. Мінаєва та інші.

Актуальність теми:

Дана тема є доповненням і поглибленням вивчення курсу геометрії.

Вивчення даної теми допоможе краще підготуватися до олімпіад і іспитів.

Мета роботи:

Ознайомитися з формулою Піка.

Оволодіти прийомами рішень геометричних задач з використанням формули Піка.

Систематизувати та узагальнити теоретичний і практичний матеріали.

Завдання дослідження:

Перевірити ефективність і доцільність застосування формули при вирішенні завдань.

Навчитися застосовувати формулу Піка в задачах різної складності.

Порівняти завдання, вирішені за допомогою формули Піка і традиційним способом.

Основна частина

1.1. Історична довідка

Георг Олександр Пік - австрійський математик, народився 10 серпня 1859 року. Він був обдарованою дитиною, його навчав батько, який очолював приватний інститут. У 16 років Георг закінчив школу і вступив до Віденського університету. У 20 років отримав право викладати фізику і математику. Всесвітню популярність йому принесла формула для визначення площі решітки полігонів. Свою формулу він опублікував в статті в 1899 році. Вона стала популярною, коли польський вчений Хьюго Штейнгауз включив її в 1969 році в видання математичних знімків.

1.2. Дослідження і доказ

В ході дослідження на різних сайтах я побачив вирішення завдань на обчислення площі п'яти-, шести-, і інших багатокутників. Формула, що дозволяє вирішувати ці завдання, називалася формулою Піка. Вона виглядає так: S \u003d B + Г / 2-1, де В - кількість вузлів, що лежать всередині багатокутника, Г- кількість вузлів, що лежать на кордоні багатокутника. Особливість цієї формули полягає в тому, що її можна застосовувати тільки для багатокутників, намальованих на картатій папері.

Щоб знайти це число, позначимо через n число сторін багатокутника, через В- число вузлів всередині нього, через Г- число вузлів на сторонах, включаючи вершини. Загальна сума кутів всіх трикутників дорівнює 180 °. Т.

Тепер знайдемо суму іншим способом.

Сума кутів з вершиною в будь-якому внутрішньому вузлі становить 2.180 °, тобто загальна сума кутів дорівнює 360 °. В;загальна сума кутів при вузлах на сторонах, але не в вершинах дорівнює ( Г-n) 180°, а сума кутів при вершинах багатокутника буде дорівнює ( Г-2) 180°. Таким чином, Т \u003d2.180 °. В + (Г-n) 180° + (n -2)180 °. Виконавши розкриття дужок і розділивши на 360 °, отримуємо формулу для площі S багатокутника, відому як формула Піка.

2. Практична частина

S \u003d 18-1,5-4,5 \u003d 12 і S \u003d 7 + 12 / 2-1 \u003d 12

S \u003d 24-9-3 \u003d 12 і S \u003d 7 + 12 / 2-1 \u003d 12

S \u003d 77-7,5-12-4,5-4 \u003d 49 і S \u003d 43 + 14 / 2-1 \u003d 49

Це підштовхнуло мене на перевірку можливості застосування формули Піка на більш складних фігурах.

S \u003d 0 + 4/2 -1 \u003d 1

S \u003d 5 + 11 / 2-1 \u003d 9,5

S \u003d 4 + 16 / 2-1 \u003d 1

висновок

Список літератури

Бунимович Е.А., Дорофєєв Г.В., Суворова С.Б. та ін. Математика. Арифметика. Геометрія. 5 клас: навч. для загальноосвіт. організацій з дод. на електрон. носії -3-е изд.-М .: Просвещение, 2014.- 223, с. : Ил. - (Сфери).

Бунимович Е.А., Кузнєцова Л.В., Мінаєва С.С. та ін. Математика. Арифметика. Геометрія. 6 клас: навч. для загальноосвіт. організацій-5-е изд.-М .: Просвещение, 2016.-240с. : Іл.- (Сфери).

Васильєв Н.Б. Навколо формули Піка. //Квант.- 1974.-№2. -с.39-43

Розсолів В.В. Завдання з планіметрії. / 5 изд., Испр. І доп. - М .: 2006.-640с.

І.В. Ященко.ОГЕ. Математика: типові екзаменаційні варіанти: О-39 36 варіантів - М .: Видавництво «Національна освіта», 2017. -240 с. - (ОГЕ. ФІПІ- школі).

«Вирішу ОГЕ»: математика. Навчальна система Дмитра Гущина. ОГЕ-2017: завдання, відповіді, рішення [Електронний ресурс]. Режим доступу: https://oge.sdamgia.ru/test?id\u003d6846966 (дата звернення 02.04.2017)

Намалюємо на картатій папері якийсь багатокутник. Наприклад, такий, як показано на малюнку 1.

Спробуємо тепер розрахувати його площу. Як це зробити? Напевно, найпростіше розбити його на прямокутні трикутники і прямокутники, площі яких вже неважко обчислити і скласти отримані результати. Використаний мною спосіб нескладний, але дуже громіздкий, крім того він годиться не для всяких багатокутників.

Розглянемо невироджених простий цілочисельний багатокутник (тобто він зв'язний - будь-які дві його точки можуть бути з'єднані безперервної кривої, цілком в ньому міститься, і все його вершини мають цілі координати, його межа - зв'язкова ламана без самоперетинів, і він має ненульову площа). Для обчислення площі такого багатокутника можна скористатися наступною теоремою:

Теорема Піка. Нехай - число цілочисельних точок всередині багатокутника, - кількість цілочисельних точок на його кордоні, - його площа. тоді справедлива формула Піка:

Приклад. Для багатокутника на малюнку 1 (жовті точки), (сині точки, не забудьте про вершинах!), Тому квадратних одиниць.

Доказ теореми Піка. Спочатку зауважимо, що формула Піка вірна для одиничного квадрата. Дійсно, в цьому випадку ми маємо і

Розглянемо прямокутник зі сторонами, що лежать на лініях решітки. Нехай довжини його сторін рівні і. Маємо в цьому випадку і, по формулі Піка,

Розглянемо тепер прямокутний трикутник з катетами, що лежать на осях координат. Такий трикутник виходить з прямокутника зі сторонами і, розглянутого в попередньому випадку, розрізанням його по діагоналі. Нехай на діагоналі лежать цілочисельних точок. Тоді для цього випадку і отримуємо, що

Тепер розглянемо довільний трикутник. Його можна отримати, відрізавши від прямокутника кілька прямокутних трикутників і, можливо, прямокутник (див. Малюнки 2 і 3). Оскільки і для прямокутника, і для прямокутного трикутника формула Піка вірна, ми отримуємо, що вона буде справедлива і для довільного трикутника.

Залишається зробити останній крок: перейти від трикутників до багатокутників. Будь багатокутник можна розбити на трикутники (наприклад, діагоналями). Тому потрібно просто довести, що при додаванні будь-якого трикутника до довільного багатокутника формула Піка залишається вірною.

Нехай багатокутник і трикутник мають спільну сторону. Припустимо, що для формула Піка справедлива, доведемо, що вона буде вірна і для багатокутника, отриманого з додаванням. Так як і мають загальну сторону, то все цілочисельні точки, що лежать на цій стороні, крім двох вершин, стають внутрішніми точками нового багатокутника. Вершини ж будуть граничними точками. Позначимо число спільних точок через і отримаємо

Число внутрішніх цілочисельних точок нового багатокутника,

Число граничних точок нового багатокутника.

З цих рівностей отримуємо

Так як ми припустили, що теорема вірна для і для окремо, то

Тим самим, формула Піка доведена.

Цю формулу відкрив австрійський математик Пік Георг Александров (1859 - 1943 р.р.) в 1899 році. Крім цієї формули Георг Пік відкрив теореми Піка, Піка - Жюліа, Піка - Неваліни, довів нерівність Шварца - Піка. В додатку 1 можна побачити розглянуті мною нестандартні завдання на застосування формули Піка.

Формула Піка

Сажина Валерія Андріївна, учнівська 9 класу МАОУ «СОШ№11» г Усть-Ілімськ Іркутської області

керівник: Губар Оксана Михайлівна, учитель математики вищої кваліфікаційної категорії МАОУ «СОШ№11» г Усть-Ілімськ Іркутської області

2016 рік

Вступ

При вивченні теми геометрії «Площі многокутників», я вирішила дізнатися: чи існує спосіб знаходження площ, відмінний від тих, які ми вивчали на уроках?

Таким способом є формула Піка. Л. В. Горіна в «Матеріалах для самоосвіти учнів» так описувала цю формулу: «Ознайомлення з формулою Піка особливо актуально напередодні здачі ЄДІ і ДПА. За допомогою цієї формули можна без проблем вирішувати великий клас задач, які пропонуються на іспитах, - це завдання на знаходження площі багатокутника, зображеного на картатій папері. Маленька формула Піка замінить цілий комплект формул, необхідних для вирішення таких завдань. Формула Піка буде працювати «одна за всіх ...»! ».

У матеріалах ЄДІ мені зустрілися завдання з практичним змістом на знаходження площі земельних ділянок. Я вирішила перевірити, чи застосовна дана формула для знаходження площі території школи, мікрорайонів міста, області. А так же раціонально її застосування для вирішення завдань.

Об'єкт дослідження: формула Піка.

Предмет дослідження: раціональність застосування формули Піка при вирішенні завдань.

Мета роботи: обґрунтувати раціональність використання формули Піка при вирішенні задач на знаходження площі фігур, зображених на картатій папері.

Методи дослідження: моделювання, порівняння, узагальнення, аналогії, вивчення літературних та Інтернет-ресурсів, аналіз і класифікація інформації.

Підібрати необхідну літературу, проаналізувати і систематизувати отриману інформацію;

Розглянути різні методи і прийоми вирішення завдань на картатій папері;

Перевірити експериментальним шляхом раціональність використання формули Піка;

Розглянути застосування даної формули.

Гіпотеза: якщо застосувати формулу Піка для знаходження площ багатокутника, то можна знайти площу території, а рішення задач на картатій папері буде більш раціонально.

Основна частина

Теоретична частина

Картата папір (точніше - її вузли), на якій ми часто вважаємо за краще малювати і креслити, є одним з найважливіших прикладів точкової решітки на площині. Уже ця проста решітка послужила К. Гауса відправною точкою для порівняння площі кола з числом точок з цілими координатами, що знаходяться всередині нього. Те, що деякі прості геометричні твердження про фігури на площині мають глибокі наслідки в арифметичних дослідженнях, було в явному вигляді помічено Г. Мінковським в 1896 р, коли він вперше для розгляду теоретико-числових проблем привернув геометричні методи.

Намалюємо на картатій папері якийсь багатокутник (Додаток 1, малюнок 1). Спробуємо тепер розрахувати його площу. Як це зробити? Напевно, найпростіше розбити його на прямокутні трикутники і трапецію, площі яких вже неважко обчислити і скласти отримані результати.

Використаний спосіб нескладний, але дуже громіздкий, крім того він годиться не для всяких багатокутників. Так наступний багатокутник можна розбити на прямокутні трикутники, так як ми це зробили в попередньому випадку (Додаток 2, малюнок 2). Можна, наприклад, спробувати доповнити його до «хорошого», потрібного нам, тобто до такого, площа якого ми зможемо обчислити описаним способом, потім з отриманого числа відняти площі доданих частин.

Однак виявляється, що є дуже проста формула, що дозволяє обчислити площі таких багатокутників з вершинами у вузлах квадратної сітки.

Ця формула залишалася непоміченою протягом деякого часу після того, як Пік її опублікував, однак в 1949 р польський математик Гуго Штейнгауз включив теорему в свій знаменитий «Математичний калейдоскоп». З цього часу теорема Піка стала широко відома. У Німеччині формула Піка включена до шкільних підручників.

Вона є класичним результатом комбінаторної геометрії і геометрії чисел.

Доведення формули Піка

Нехай АВСD - прямокутник з вершинами у вузлах і сторонами, що йдуть по лініях сітки (Додаток 3, малюнок 3).

Позначимо через В - кількість вузлів, що лежать всередині прямокутника, а через Г - кількість вузлів на його кордоні. Змістимо сітку на полклеткі вправо і полклеткі

вниз. Тоді територію прямокутника можна «розподілити» між вузлами в такий спосіб: кожен з В вузлів «контролює» цілу клітку зміщеною сітки, а кожен з Г вузлів - 4 граничних НЕ кутових вузла - половину клітини, а кожна з кутових точок - чверть клітини. Тому площа прямокутника S дорівнює

S \u003d В + + 4 · \u003d В + - 1 .

Отже, для прямокутників з вершинами у вузлах і сторонами, що йдуть по лініях сітки, ми встановили формулу S \u003d В + - 1 . Це і є формула Піка.

Виявляється, ця формула вірна не тільки для прямокутників, а й для довільних багатокутників з вершинами у вузлах сітки.

Практична частина

Знаходження площі фігур геометричним методом і за формулою Піка

Я вирішила переконатися в тому, що формула Піка вірна для всіх розглянутих прикладів.

Виявляється, що якщо багатокутник можна розрізати на трикутники з вершинами у вузлах сітки, то для нього вірна формула Піка.

Я розглянула деякі завдання на картатій папері з клітинами розміром 1 см1 см і провела порівняльний аналіз за рішенням завдань (Таблиця № 1).

Таблиця № 1 Рішення задач різними способами.

малюнок

За формулою геометрії

За формулою Піка

завдання №1

S \u003d S пр - (2S 1 + 2S 2 )

S пр =4*5=20 см 2

S 1 =(2*1)/2=1 см 2

S 2 =(2*4)/2=4 см 2

S \u003d 20 (2 * 1 + 2 * 4) \u003d 10см 2

відповідь :10 см ².

В \u003d 8, Г \u003d 6

S \u003d 8 + 6/2 - 1 \u003d 10 (см)

Відповідь: 10 см².

завдання №2

a \u003d 2, h \u003d 4

S \u003d a * h \u003d 2 * 4 \u003d 8см 2

відповідь : 8 см ².

В \u003d 6, Г \u003d 6

S \u003d 6 + 6/2 - 1 \u003d 8 (см)

Відповідь: 8 см².

завдання №3

S \u003d S кв - (S 1 + 2S 2 )

S кв =4 2 =16 см 2

S 1 \u003d (3 * 3) / 2 \u003d 4,5 см 2

S 2 \u003d (1 * 4) / 2 \u003d 2см 2

S\u003d 16- (4,5 + 2 * 2) \u003d 7.5 см 2

В \u003d 6, Г \u003d 5

S \u003d 6 + 5/2 - 1 \u003d 7,5 (см)

Відповідь: 7,5 см².

завдання №4

S \u003d S пр - (S 1 + S 2+ S 3 )

S пр =4 * 3=12 см 2

S 1 =(3*1)/2=1,5 см 2

S 2 =(1*2)/2=1 см 2

S 3 =(1+3)*1/2=2 см 2

S \u003d 12- (1,5 + 1 + 2) \u003d 7.5см 2

В \u003d 5, Г \u003d 7

S \u003d 5 + 7/2 - 1 \u003d 7,5 (см)

Відповідь: 7,5 см².

завдання № 5.

S \u003d S пр - (S 1 + S 2+ S 3 )

S пр =6 * 5=30 см 2

S 1 =(2*5)/2=5 см 2

S 2 =(1*6)/2=3 см 2

S 3 =(4*4)/2=8 см 2

S \u003d 30- (5 + 3 + 8) \u003d 14см 2

Відповідь: 14 см²

В \u003d 12, Г \u003d 6

S \u003d 12 + 6/2 - 1 \u003d 14 (см)

Відповідь: 14 см²

завдання №6.

S тр \u003d (4 + 9) / 2 * 3 \u003d 19,5 см 2

Відповідь: 19,5 см 2

В \u003d 12, Г \u003d 17

S \u003d 12 + 17/2 - 1 \u003d 19,5 (см)

Відповідь: 19,5 см 2

завдання №7. Знайдіть площу лісового масиву (в м²), зображеного на плані з квадратною сіткою 1 × 1 (см) в масштабі 1 см - 200 м

S \u003d S 1 + S 2+ S 3

S 1 =(800*200)/2=80000 м 2

S 2 =(200*600)/2=60000 м 2

S 3 =(800+600)/2*400=

280000 м 2

S \u003d80000+60000+240000=

420000м 2

Відповідь: 420 000 м²

В \u003d 8, Г \u003d 7. S \u003d 8 + 7/2 - 1 \u003d 10,5 (см)

1 см² - 200² м²; S \u003d 40000 · 10,5 \u003d 420 000 (м²)

Відповідь: 420 000 м²

завдання №8 . Знайдіть площу поля (в м²), зображеного на плані з квадратною сіткою 1 × 1 (см) в масштабі

1 см - 200 м.

S= S кв -2 ( S тр + S трап)

S кв \u003d 800 * 800 \u003d 640000 м 2

S тр \u003d (200 * 600) / 2 \u003d 60000м 2

S трап \u003d (200 + 800) / 2 * 200 \u003d

100000м 2

S=640000-2(60000+10000)=

320000 м 2

Відповідь: 320 000 м²

Рішення. знайдемо S площа чотирикутника, зображеного на картатій папері за формулою Піка:S \u003d В + - 1

В \u003d 7, Г \u003d 4. S \u003d 7 + 4/2 - 1 \u003d 8 (см)

1 см² - 200² м²; S \u003d 40000 · 8 \u003d 320 000 (м²)

Відповідь: 320 000 м²

завдання №9 . Знайдіть площуS сектора, вважаючи боку квадратних клітин рівними 1. У відповіді вкажіть .

Сектор є однією четвертою частиною кола і, отже, його площа дорівнює одній четвертій площі кола. Площа круга дорівнює πR 2 , де R - радіус кола. У нашому випадкуR =√5 і, отже, площаS сектора дорівнює 5π / 4. ЗвідкиS/ Π \u003d 1,25.

Відповідь. 1,25.

Г \u003d 5, В \u003d 2, S \u003d В + Г / 2 - 1 \u003d 2 + 5/2 - 1 \u003d 3,5, ≈ 1,11

Відповідь. 1,11.

Завдання №10. Знайдіть площу S кільця, вважаючи боку квадратних клітин рівними 1. У відповіді вкажіть .

Площа кільця дорівнює різниці площ зовнішнього і внутрішнього кіл. радіусR зовнішнього кола дорівнює

2, радіус r внутрішнього кола дорівнює 2. Отже, площа кільця дорівнює 4 і, отже, . Відповідь: 4.

Г \u003d 8, В \u003d 8, S \u003d В + Г / 2 - 1 \u003d 8 + 8/2 - 1 \u003d 11, ≈ 3,5

Відповідь: 3,5

Висновки: Розглянуті завдання аналогічні завданням з варіантів контрольно-вимірювальних матеріалів ЄДІ з математики (завдання №5,6) ,.

З розглянутих рішень задач я побачила, що деякі з них, наприклад завдання № 2,6, легше вирішити, застосовуючи геометричні формули, так як висоту і підстава можна визначити по малюнку. Але в більшості завдань потрібно розбиття фігури на більш прості (завдання №7) або добудовування до прямокутника (завдання №1,4,5), квадрата (завдання №3,8).

З вирішення завдань №9 і №10 я побачила, що застосування формули Піка до фігур, які не є багатокутниками, дає наближений результат.

Для того, щоб перевірити раціональність використання формули Піка, я провела дослідження на предмет витраченого часу (Додаток 4, таблиця №2).

Висновок: з таблиці і діаграми (Додаток 4, діаграма 1) видно, що при вирішенні завдань за допомогою формули Піка, часу витрачається набагато менше.

Знаходження площі поверхні просторових форм

Перевіримо придатність цієї формули до просторовим формам (Додаток 5, малюнок 4).

Знайти площу повної поверхні прямокутного паралелепіпеда, вважаючи боку квадратних клітин рівними 1.

Це недолік формули.

Застосування формули Піка для знаходження площі території

Вирішуючи завдання з практичним змістом, (завдання №7,8; таблиця №1), я вирішила застосувати цей спосіб для знаходження площі території нашої школи, мікрорайонів міста Усть-Ілімськ, Іркутської області.

Ознайомившись з «Проектом меж земельної ділянки МАОУСОШ№11 Усть-Ілімськ» (Додаток 6) ,, я знайшла площа території нашої школи і порівняла з площею по проекту меж земельної ділянки (Додаток 9, таблиця 3).

Розглянувши карту правобережної частини Усть-Ілімськ (Додаток 7) ,, я вирахувала площі мікрорайонів і порівняла з даними з «Генерального плану м Усть-Ілімськ Іркутської області». Результати представила в таблиці (Додаток 9, таблиця 4).

Розглянувши карту Іркутської області (Додаток 7) ,, я знайшла площа території і порівняла з даними з Вікіпедії. Результати представила в таблиці (Додаток 9, таблиця 5).

Проаналізувавши результати, я прийшла до висновку: за формулою Піка ці площі можна знайти набагато простіше, але результати приблизні.

З проведених досліджень найбільш точне значення я отримала під час перебування площі території школи (Додаток 10, діаграма 2). Більша розбіжність в результатах вийшло при знаходженні площі Іркутської області (Додаток 10, діаграма 3). Це пов'язано з тим. Що не всі межі області є сторонами багатокутників, і вершини не є вузловими точками.

висновок

В результаті моєї роботи я розширила свої знання про рішення задач на картатій папері, визначила для себе класифікацію досліджуваних задач.

При виконанні роботи були вирішені завдання на знаходження площі багатокутників, зображених на картатій папері двома способами: геометричним і за допомогою формули Піка.

Аналіз рішень і експеримент по визначенню витраченого часу показав, що застосування формули дає можливість вирішувати завдання на знаходження площі багатокутника, більш раціонально. Це дозволяє економити час на ЄДІ з математики.

Знаходження площі різних фігур, зображених на картатій папері, дозволило зробити висновок, що використання формули Піка для обчислення площі кругового сектора і кільця недоцільно, так як вона дає наближений результат, і, що формула Піка не застосовується для вирішення завдань в просторі.

Так само в роботі були знайдені площі різних територій за формулою Піка. Можна зробити висновок: використання формули для знаходження площі різних територій можливо, але результати виходять приблизними.

Висунута мною гіпотеза підтвердилася.

Я прийшла до висновку, що тема, яка мене зацікавила, досить багатогранна, завдання на картатій папері різноманітні, методи і прийоми їх вирішення також різноманітні. Тому я вирішила продовжити роботу в цьому напрямку.

література

Волков С.Д .. Проект меж земельної ділянки, 2008 р, с. 16.

Горіна Л.В., Математика. Все для вчителя, М: Наука, 2013 р .. №3, с. 28.

Прокоп'єва В.П., Петров А.Г., Генеральний план міста Усть-Ілімськ Іркутської області, Держбуд Росії, 2004 р .. с. 65.

Рісс Е. А., Жарковський Н. М., Геометрія картатій паперу. Формула Піка. - Москва, 2009, № 17, с. 24-25.

Смирнова І. М.,. Смирнов В. А, Геометрія на картатій папері. - Москва, Чисті ставки, 2009, с. 120.

Смирнова І. М., Смирнов В. А., Геометричні завдання з практичним змістом. - Москва, Чисті ставки, 2010, с. 150

Завдання відкритого банку завдань з математики ФІПІ, 2015.

Карта міста Усть-Ілімськ.

Карта Іркутської області.

Вікіпедія.

Творча робота "застосування формули піку". геометрія

бібліографічна посилання

Вступ

Основна частина

Теоретична частина

Доведення формули Піка

Практична частина

Знаходження площі фігур геометричним методом і за формулою Піка

Знаходження площі поверхні просторових форм

Застосування формули Піка для знаходження площі території

висновок

література

Рекомендуємо інші статті

З чого складаються кістки. Приватна анатомія. вчення про кістки - остеологія Будова і види кісткової тканини. кісткові тканини

Твір приклади співчуття з життя