Vektor. Grunnleggende egenskaper

Definisjon En ordnet samling (x 1, x 2, ..., x n) n reelle tall kalles n-dimensjonal vektor, og tallene x i (i = 1, ..., n) er komponenter eller koordinater,

Eksempel. Hvis for eksempel et bestemt bilfabrikk må produsere 50 biler, 100 lastebiler, 10 busser, 50 sett med reservedeler for biler og 150 sett for lastebiler og busser per skift, kan produksjonsprogrammet til dette anlegget skrives i form av en vektor (50, 100, 10, 50, 150) som har fem komponenter.

Notasjon. Vektorer er merket med fete små bokstaver eller bokstaver med en stolpe eller pil øverst, for eksempel, en eller . De to vektorene kalles lik hvis de har samme antall komponenter og deres tilsvarende komponenter er like.

Vektorkomponenter kan ikke byttes, for eksempel er (3, 2, 5, 0, 1) og (2, 3, 5, 0, 1) forskjellige vektorer.
Operasjoner på vektorer. Etter produktx= (x 1, x 2, ..., x n) med et reelt tall λ kalles en vektor λ x= (λ x 1, λ x 2, ..., λ x n).

Summenx= (x 1, x 2, ..., x n) og y= (y 1, y 2, ..., y n) kalles vektoren x + y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

Rom av vektorer. N-dimensjonalt vektorrom R n er definert som settet av alle n-dimensjonale vektorer for hvilke operasjonene multiplikasjon med reelle tall og addisjon er definert.

Økonomisk illustrasjon. Økonomisk illustrasjon av n-dimensjonalt vektorrom: plass av varer (varer). Under handelsvare vi vil forstå noen varer eller tjenester som ble solgt på et bestemt tidspunkt på et bestemt sted. Anta at det er et begrenset antall gjenstander tilgjengelig, n; mengdene av hver av dem kjøpt av forbrukeren er preget av et sett med varer

x= (x 1, x 2, ..., x n),

hvor x i angir mengden av den i-te varen kjøpt av forbrukeren. Vi vil anta at alle varer har egenskapen til vilkårlig delbarhet, slik at enhver ikke-negativ mengde av hver av dem kan kjøpes. Da er alle mulige sett med varer vektorer av varerommet C = ( x= (x 1, x 2, ..., x n) x i ≥ 0, i = 1, ..., n).

Lineær uavhengighet. System e 1 , e 2 , ... , e m n-dimensjonale vektorer kalles lineært avhengig hvis det er tall λ 1, λ 2, ..., λ m slik at minst ett av dem ikke er null slik at λ 1 e 1 + λ m e m = 0; ellers kalles dette systemet av vektorer lineært uavhengig, det vil si at den indikerte likheten er mulig bare i tilfellet når alle λ 1 = λ 2 = ... = λ m = 0. Den geometriske betydningen av den lineære avhengigheten til vektorer i R 3, tolket som rettet segmenter, forklar følgende teoremer.

Teorem 1. Et system som består av én vektor er lineært avhengig hvis og bare hvis denne vektoren er null.

Teorem 2. For at to vektorer skal være lineært avhengige, er det nødvendig og tilstrekkelig at de er kollineære (parallelle).

Teorem 3 ... For at tre vektorer skal være lineært avhengige, er det nødvendig og tilstrekkelig at de er koplanære (ligger i samme plan).

Venstre og høyre trillinger av vektorer. Tre ikke-koplanare vektorer a, b, c kalt Ikke sant hvis observatøren fra deres felles opphav krysser endene av vektorene a, b, c i den viste rekkefølgen ser det ut til å være med klokken. Ellers a, b, c -venstre trippel... Alle høyre (eller venstre) trillinger av vektorer kalles likt orientert.

Grunnlag og koordinater. Troika e 1, e 2 , e 3 ikke-koplanare vektorer i R 3 kalles basis, og selve vektorene e 1, e 2 , e 3 - grunnleggende... Enhver vektor en kan utvides unikt når det gjelder basisvektorer, det vil si representert i formen

en= x 1 e 1 + x 2 e 2 + x 3 e 3, (1.1)

tallene x 1, x 2, x 3 i utvidelsen (1.1) kalles koordinateren i grunnlaget e 1, e 2 , e 3 og er betegnet en(x 1, x 2, x 3).

Ortonormal basis. Hvis vektorer e 1, e 2 , e 3 er parvis vinkelrette og lengden på hver av dem er lik en, så kalles grunnlaget ortonormal, og koordinater x 1, x 2, x 3 - rektangulær. Basisvektorene til den ortonormale basisen vil bli betegnet med i, j, k.

Vi vil anta det i verdensrommet R 3 er det høyre systemet med kartesiske rektangulære koordinater valgt (0, i, j, k}.

Vektor produkt.Vektor produkten per vektor b kalles en vektor c, som bestemmes av følgende tre forhold:

1. Vektorlengde c er numerisk lik arealet til et parallellogram bygget på vektorer en og b, dvs.
c= | a || b | synd ( en^b).

2. Vektor c vinkelrett på hver av vektorene en og b.

3. Vektorer en, b og c tatt i den angitte rekkefølgen fra en høyre trilling.

For vektorprodukt c notasjonen introduseres c =[ab] eller
c = a × b.

Hvis vektorer en og b collinear, så synd ( a ^ b) = 0 og [ ab] = 0, spesielt, [ aa] = 0. Vektorprodukter av enhetsvektorer: [ ij]=k, [jk] = Jeg, [ki]=j.

Hvis vektorer en og b gitt i grunnlaget i, j, k koordinater en(en 1, en 2, en 3), b(b 1, b 2, b 3), deretter

Blandet arbeid. Hvis kryssproduktet av to vektorer en og b skalar multiplisert med den tredje vektoren c, da kalles et slikt produkt av tre vektorer blandet arbeid og er merket med symbolet en b c.

Hvis vektorer a, b og c i grunnlaget i, j, k gitt av deres koordinater
en(en 1, en 2, en 3), b(b 1, b 2, b 3), c(c 1, c 2, c 3), deretter

.

Det blandede produktet har en enkel geometrisk tolkning - det er en skalar som i absolutt verdi er lik volumet til et parallellepiped bygget på disse tre vektorene.

Hvis vektorene danner en høyre-triplett, er deres blandede produkt et positivt tall lik det indikerte volumet; hvis de tre a, b, c - venstre da a b c<0 и V = - a b c, derfor V = | a b c |.

Koordinatene til vektorene som påtreffes i oppgavene i første kapittel antas å være gitt med hensyn til rett ortonormalt grunnlag. Enhetsvektor codirectional til vektor en, angitt med symbolet en O. Symbol r=OM angitt med radiusvektoren til punktet M, symbolene a, AB eller | a |, |AB | modulene til vektorer en og AB.

Eksempel 1.2. Finn vinkelen mellom vektorer en= 2m+4n og b= m-n, hvor m og n - enhetsvektorer og vinkel mellom m og n er lik 120 p.

Løsning... Vi har: cos φ = ab/ ab, ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4 + 2cos120 o = - 2 + 2 (-0,5) = -3; a = ; en 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4 + 16 (-0,5) + 16 = 12, så a =. b = ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 = 1-2 (-0,5) +1 = 3, så b =. Til slutt har vi: cos φ == -1/2, φ = 120 o.

Eksempel 1.3. Kjenne til vektorer AB(-3, -2,6) og f.Kr(-2,4,4), beregn lengden på høyden AD til trekanten ABC.

Løsning... Ved å angi arealet av trekanten ABC til S, får vi:
S = 1/2 f.Kr. e.Kr. Da AD = 2S / BC, BC = = = 6,
S = 1/2 | AB ×AC |. AC = AB + BC, altså vektoren AC har koordinater
.

DEFINISJON

Vektor(fra lat." vektor"-" peiling ") - et rettet segment av en rett linje i rommet eller på et plan.

Grafisk er en vektor avbildet som et rettet linjestykke av en viss lengde. En vektor, hvis begynnelse er ved et punkt, og slutten på et punkt, er betegnet som (fig. 1). En vektor kan også betegnes med en liten bokstav, for eksempel.

Hvis et koordinatsystem er spesifisert i rommet, kan vektoren spesifiseres unikt av et sett med dens koordinater. Det vil si at en vektor forstås som et objekt som har en størrelse (lengde), retning og påføringspunkt (vektorens begynnelse).

Begynnelsen av vektorregning dukket opp i verk i 1831 i verkene til den tyske matematikeren, mekanikeren, fysikeren, astronomen og landmåleren Johann Karl Friedrich Gauss (1777-1855). Artikler om operasjoner med vektorer ble publisert av den irske matematikeren, mekanikeren og teoretisk fysikeren Sir William Rowan Hamilton (1805-1865) innenfor rammen av hans kvartærnionregning. Forskeren foreslo begrepet "vektor" og beskrev noen operasjoner på vektorer. Vektorkalkulus ble videreutviklet takket være arbeidet med elektromagnetisme av den britiske fysikeren, matematikeren og mekanikeren James Clerk Maxwell (1831-1879). På 1880-tallet ble boken «Elements of Vector Analysis» utgitt av den amerikanske fysikeren, fysikokjemikeren, matematikeren og mekanikeren Josiah Willard Gibbs (1839-1903). Moderne vektoranalyse ble beskrevet i 1903 av den engelske selvlærte vitenskapsmannen, ingeniøren, matematikeren og fysikeren Oliver Heaviside (1850-1925).

DEFINISJON

Lengde eller vektor modul er lengden på det rettede segmentet som definerer vektoren. Det er angitt som.

Grunnleggende typer vektorer

Null vektor er en vektor hvis startpunkt og sluttpunkt faller sammen. Lengden på nullvektoren er null.

Vektorer som er parallelle med en rett linje eller som ligger på en rett linje kalles kollineær(fig. 2).

co-regissert hvis retningene deres er de samme.

I figur 2 er dette vektorer og. Samdireksjonaliteten til vektorer er angitt som følger:.

To kollineære vektorer kalles motsatt rettet hvis retningene deres er motsatte.

I figur 3 er dette vektorer og. Betegnelse:.

VEKTORER... HANDLINGEROVENFORVEKTORER. SKALAR,

VEKTOR, BLANDET PRODUKT AV VEKTORER.

1. VEKTORER, HANDLINGER PÅ VEKTORER.

Grunnleggende definisjoner.

Definisjon 1. En størrelse som er fullt preget av sin numeriske verdi i det valgte enhetssystemet kalles skalar eller skalar .

(Kroppsvekt, volum, tid osv.)

Definisjon 2. En størrelse karakterisert ved en numerisk verdi og retning kalles vektor eller vektor .

(Forskyvning, styrke, hastighet, etc.)

Betegnelser:, eller,.

En geometrisk vektor er en retningslinje.

For en vektor - et punkt EN- startpunkt V- slutten av vektoren.

Definisjon 3.Modul vektor er lengden på segmentet AB.

Definisjon 4. En vektor hvis modul er lik null kalles null , indikert av.

Definisjon 5. Vektorer som ligger på parallelle linjer eller på én linje kalles kollineær ... Hvis to kollineære vektorer har samme retning, kalles de co-regissert .

Definisjon 6. To vektorer vurderes lik , hvis de co-regissert og er like i absolutt verdi.

Handlinger på vektorer.

1) Addisjon av vektorer.

Def. 6.Summen to vektorer og er diagonalen til parallellogrammet bygget på disse vektorene, med utgangspunkt i det felles punktet for deres anvendelse (parallelogramregel).

Figur 1.

Def. 7. Summen av tre vektorer,, kalles diagonalen til parallellepipedet bygget på disse vektorene (boksregel).

Def. åtte. Hvis EN, V, MED - vilkårlige punkter, deretter + = (trekantregel).

fig. 2

Tilleggsegenskaper.

1 O . + = + (transposisjonslov).

2 O . + (+) = (+) + = (+) + (kombinasjonslov).

3 O . + (– ) + .

2) Subtraksjon av vektorer.

Def. ni. Under forskjell vektorer og forstå vektor = - slik at + = .

I et parallellogram er dette en annen diagonal SD (se figur 1).

3) Multiplisere en vektor med et tall.

Def. ti. Etter produkt vektorer per skalar k kalles en vektor

= k = k ,

lang ka , og hvilken retning:

1.sammenfaller med retningen til vektoren if k > 0;

2. Motsatt av retningen til vektoren, if k < 0;

3. vilkårlig hvis k = 0.

Egenskaper ved å multiplisere en vektor med et tall.

1 O . (k + l ) = k + l .

k ( + ) = k + k .

2 o . k (l ) = (kl ) .

3 o . 1  = , (–1)  = – , 0  = .

Vektoregenskaper.

Def. elleve. To vektorer og kalles kollineær hvis de er plassert på parallelle linjer eller på en rett linje.

En nullvektor er kollineær til enhver vektor.

Teorem 1. To ikke-null vektorer og collineær,  når de er proporsjonale dvs.

= k , k Er en skalar.

Def. 12. Tre vektorer,, kalles koplanar hvis de er parallelle med et eller annet plan eller ligger i det.

Teorem 2. Tre vektorer som ikke er null,, coplanar,  når en av dem er en lineær kombinasjon av de to andre, dvs.

= k + l , k , l - skalarer.

Projeksjonen av vektoren til aksen.

Teorem 3. Projeksjon av en vektor på en akse (rettet rett linje) l er lik produktet av lengden til vektoren og cosinus til vinkelen mellom retningen til vektoren og retningen til aksen, dvs. = en  c os  ,  = ( , l).

2. VEKTORKOORDINATER

Def. 1. 3. Vektorprojeksjoner på koordinatakser Åh, OU, Оz er kalt vektorkoordinater. Betegnelse:  en x , en y , en z .

Vektorlengde:

Eksempel: Regn ut lengden på vektoren.

Løsning:

Avstand mellom punktene og beregnet med formelen: .

Eksempel: Finn avstanden mellom punktene M (2,3, -1) og K (4,5,2).

Handlinger på vektorer i koordinatform.

Oppgitte vektorer =  en x , en y , en z og =  b x , b y , b z .

1. (  )= en x  b x , en y  b y , en z  b z .

2.  =   en x ,  en y ,  en z, hvor  Er en skalar.

Punktprodukt av vektorer.

Definisjon: Under punktproduktet av to vektorer og

forstås som et tall lik produktet av lengdene til disse vektorene med cosinus til vinkelen mellom dem, dvs. = , er vinkelen mellom vektorer og.

Punkt produktegenskaper:

1.  =

2. ( + ) =

3.

4.

5. , hvor er skalarer.

6.to vektorer er perpendikulære (ortogonale) if .

7.hvis og bare hvis .

Punktproduktet i koordinatform er: , hvor og .

Eksempel: Finn punktproduktet av vektorer og

Løsning:

Vektor holder vektorer.

Definisjon: Vektorproduktet av to vektorer forstås som en vektor som:

Modulen er lik arealet til parallellogrammet bygget på disse vektorene, dvs. , hvor vinkelen mellom vektorer og

Denne vektoren er vinkelrett på vektorene som multipliseres, dvs.

Hvis vektorene ikke er kollineære, danner de den rette tripletten av vektorer.

Vektor produktegenskaper:

(1) Når rekkefølgen av faktorene endres, endrer vektorproduktet fortegn til det motsatte, og bevarer modulen, dvs.

2 .Vektorkvadraten er lik nullvektoren, dvs.

3 Skalarfaktoren kan flyttes utenfor tegnet til vektorproduktet, dvs.

4 For alle tre vektorer, likheten

5 En nødvendig og tilstrekkelig betingelse for kollinearitet av to vektorer og:

Vektorprodukt i koordinatform.

Hvis koordinatene til vektorene og , deretter deres kryssprodukt er funnet av formelen:

.

Så fra definisjonen av et vektorprodukt følger det at arealet til et parallellogram bygget på vektorer og beregnes av formelen:

Eksempel: Beregn arealet av en trekant med hjørner (1; -1; 2), (5; -6; 2), (1; 3; -1).

Løsning: .

Da vil arealet av trekanten ABC beregnes som følger:

,

Blandet produkt av vektorer.

Definisjon: Et blandet (vektor-skalar) produkt av vektorer er et tall bestemt av formelen: .

Blandede arbeidsegenskaper:

1. Blandingsproduktet endres ikke under syklisk permutasjon av dets faktorer, dvs. .

2. Ved permutasjon av to tilstøtende faktorer endrer det blandede produktet fortegn til det motsatte, dvs. ...

3 En nødvendig og tilstrekkelig betingelse for koplanariteten til tre vektorer : =0.

4 Blandingsproduktet av tre vektorer er lik volumet til parallellepipedet bygget på disse vektorene, tatt med et plusstegn dersom disse vektorene danner en høyre trippel, og med et minustegn hvis de danner en venstre trippel, dvs. .

Om kjent koordinater vektorer , så blir det blandede verket funnet av formelen:

Eksempel: Regn ut det blandede produktet av vektorer.

Løsning:

3. Grunnlaget for systemet av vektorer.

Definisjon. Et system av vektorer forstås som flere vektorer som tilhører samme rom R.

Kommentar. Hvis systemet består av et begrenset antall vektorer, er de merket med samme bokstav med forskjellige indekser.

Eksempel.

Definisjon. Enhver vektor av formen = kalles en lineær kombinasjon av vektorer. Tallene er koeffisientene til den lineære kombinasjonen.

Eksempel. .

Definisjon... Hvis vektoren er en lineær kombinasjon av vektorer , da sies vektoren å være lineært uttrykt i form av vektorer .

Definisjon. Vektorsystemet kalles lineært uavhengig hvis ingen av vektorene i systemet kan være som en lineær kombinasjon av resten av vektorene. Ellers kalles systemet lineært avhengig.

Eksempel... Vektorsystem lineært avhengig, siden vektoren .

Fastsettelse av grunnlaget. Et system av vektorer danner et grunnlag hvis:

1) den er lineært uavhengig,

2) enhver romvektor uttrykkes lineært gjennom den.

Eksempel 1. Plassgrunnlag:.

2. I systemet av vektorer vektorer er grunnlaget: er lineært uttrykt i form av vektorer.

Kommentar. For å finne grunnlaget for et gitt vektorsystem, må du:

1) skriv koordinatene til vektorene inn i matrisen,

2) bruke elementære transformasjoner for å bringe matrisen til en trekantet form,

3) rader som ikke er null i matrisen vil være grunnlaget for systemet,

4) antall vektorer i grunnlaget er lik rangeringen av matrisen.

Det vil være oppgaver for uavhengig avgjørelse som du kan se svarene på.

Vektor konsept

Før du lærer alt om vektorer og operasjoner på dem, må du prøve å løse et enkelt problem. Det er en vektor for ditt entreprenørskap og en vektor for dine innovative evner. Entreprenørskapsvektoren leder deg til mål 1, og vektoren for innovative evner fører til mål 2. Spillereglene er slik at du ikke kan bevege deg i retningene til disse to vektorene samtidig og oppnå to mål på en gang. Vektorer samhandler, eller, i matematiske termer, noen operasjoner utføres på vektorer. Resultatet av denne operasjonen er "Resultat"-vektoren, som fører deg til mål 3.

Fortell meg nå: Resultatet av hvilken operasjon på vektorene "Enterprise" og "Innovative evner" er vektoren "Resultat"? Hvis du ikke kan si det med en gang, ikke bli motløs. Etter hvert som du går gjennom denne leksjonen, vil du kunne svare på dette spørsmålet.

Som vi allerede har sett ovenfor, går vektoren nødvendigvis fra et punkt EN i en rett linje til et punkt B... Derfor har hver vektor ikke bare en numerisk verdi - lengde, men også fysisk og geometrisk - retning. Dette fører til den første og enkleste definisjonen av en vektor. Så en vektor er et rettet segment som går fra et punkt EN til punktet B... Den er betegnet som følger:.

Og å starte annerledes vektoroperasjoner , må vi bli kjent med enda en vektordefinisjon.

En vektor er en slags representasjon av et punkt du ønsker å komme til fra et eller annet utgangspunkt. For eksempel skrives en tredimensjonal vektor vanligvis som (x, y, z) . Ganske enkelt representerer disse tallene hvor langt det tar å reise i tre forskjellige retninger for å komme til et punkt.

La en vektor gis. Hvori x = 3 (høyre hånd peker mot høyre) y = 1 (venstre hånd peker fremover) z = 5 (under punktet er det en trapp som fører opp). I følge disse dataene vil du finne et punkt ved å gå 3 meter i retningen angitt av høyre hånd, deretter 1 meter i retningen angitt av venstre hånd, og deretter venter en trapp på deg, og når du klatrer 5 meter, vil du til slutt finne deg selv på det siste punktet.

Alle andre termer er forbedringer av forklaringen ovenfor, nødvendige for ulike operasjoner på vektorer, det vil si å løse praktiske problemer. La oss gå gjennom disse strengere definisjonene, og dvele ved typiske vektorproblemer.

Fysiske eksempler vektormengder kan være forskyvningen av et materialpunkt som beveger seg i rommet, hastigheten og akselerasjonen til dette punktet, samt kraften som virker på det.

Geometrisk vektor presentert i todimensjonalt og tredimensjonalt rom i skjemaet retningssegment... Dette er et segment som skiller mellom begynnelsen og slutten.

Hvis EN er begynnelsen av vektoren, og B- slutten, så er vektoren angitt med et symbol eller en liten bokstav. På figuren er slutten av vektoren indikert med en pil (fig. 1)

Lengde(eller modul) av en geometrisk vektor er lengden på segmentet som genererer den

De to vektorene kalles lik , hvis de kan justeres (hvis retningene faller sammen) ved hjelp av parallell overføring, dvs. hvis de er parallelle, peker de i samme retning og har like lange.

I fysikk blir det ofte vurdert forankrede vektorer gitt av påføringspunkt, lengde og retning. Hvis applikasjonspunktet for vektoren ikke spiller noen rolle, kan den overføres, og opprettholde lengden og retningen til et hvilket som helst punkt i rommet. I dette tilfellet kalles vektoren gratis... Vi er enige om kun å vurdere gratis vektorer.

Lineære operasjoner på geometriske vektorer

Multiplisere en vektor med et tall

Produkt av vektor etter nummeret kalles en vektor hentet fra en vektor ved å strekke (at) eller kompresjon (at) etter tider, og retningen til vektoren bevares, if, og endres til det motsatte, if. (Fig. 2)

Det følger av definisjonen at vektorene og = alltid er plassert på en eller på parallelle linjer. Slike vektorer kalles kollineær... (Du kan også si at disse vektorene er parallelle, men i vektoralgebra er det vanlig å si "kollineær".) Det motsatte er også sant: hvis vektorer og er kollineære, så er de relatert av relasjonen

Derfor uttrykker likhet (1) kollinearitetsbetingelsen for to vektorer.

Addisjon og subtraksjon av vektorer

Når du legger til vektorer, må du vite det sum vektorer og kalles en vektor, hvis begynnelse faller sammen med begynnelsen av vektoren, og slutten - med slutten av vektoren, forutsatt at begynnelsen av vektoren er festet til slutten av vektoren. (Fig. 3)

Denne definisjonen kan fordeles over et hvilket som helst begrenset antall vektorer. La det gis plass n gratis vektorer. Når du legger til flere vektorer, tas den avsluttende vektoren som summen, hvor begynnelsen sammenfaller med begynnelsen av den første vektoren, og slutten - med slutten av den siste vektoren. Det vil si hvis du fester begynnelsen av vektoren til slutten av vektoren, og begynnelsen av vektoren til slutten av vektoren osv. og til slutt, til slutten av vektoren - begynnelsen av vektoren, så er summen av disse vektorene den avsluttende vektoren hvis begynnelse faller sammen med begynnelsen av den første vektoren, og slutten - med slutten av den siste vektoren. (Fig. 4)

Begrepene kalles komponentene til vektoren, og den formulerte regelen er polygonregel... Denne polygonen er kanskje ikke flat.

Når du multipliserer en vektor med -1, får du den motsatte vektoren. Vektorene og har samme lengde og motsatte retninger. Summen deres gir null vektor hvis lengde er null. Retningen til nullvektoren er udefinert.

I vektoralgebra er det ikke nødvendig å vurdere subtraksjonsoperasjonen separat: å subtrahere en vektor fra en vektor betyr å legge til den motsatte vektoren til vektoren, dvs.

Eksempel 1. Forenkle uttrykk:

.

,

det vil si at vektorer kan adderes og multipliseres med tall på samme måte som polynomer (spesielt også oppgaver om å forenkle uttrykk). Vanligvis oppstår behovet for å forenkle lineært lignende uttrykk med vektorer før man beregner produktene til vektorer.

Eksempel 2. Vektorene og tjener som diagonalene til parallellogrammet ABCD (fig. 4a). Uttrykk i form av begge vektorer, og, som er sidene av dette parallellogrammet.

Løsning. Skjæringspunktet for parallellogramdiagonalene deler hver diagonal i to. Vi finner lengdene på vektorene som kreves i problemformuleringen enten som halvparten av summene av vektorene som danner en trekant med de ønskede, eller som halvparten av forskjellene (avhengig av retningen til vektoren som tjener som diagonal), eller som i sistnevnte tilfelle, halve summen tatt med et minustegn. Resultatet er vektorene som kreves i problemformuleringen:

Det er all grunn til å tro at du nå har svart riktig på spørsmålet om Entreprenørskap og Innovasjonsevne-vektorene i begynnelsen av denne leksjonen. Riktig svar: addisjonsoperasjon utføres på disse vektorene.

Løs vektorproblemer selv og se løsninger

Hvordan finne lengden på summen av vektorer?

Denne oppgaven tar en spesiell plass i vektoroperasjoner, da den involverer bruk av trigonometriske egenskaper. La oss si at du kommer over en oppgave som følgende:

Gitt lengdene til vektorene og lengden på summen av disse vektorene. Finn lengden på forskjellen mellom disse vektorene.

Løsninger for dette og andre lignende oppgaver og en forklaring på hvordan du løser dem - i leksjonen " Vektoraddisjon: vektorsumlengde og cosinussetning ".

Og du kan sjekke løsningen av slike problemer på Online kalkulator "Ukjent side av en trekant (vektoraddisjon og cosinus-teorem)" .

Hvor er produktene til vektorer?

Vektor-for-vektor-produktene er ikke lineære operasjoner og vurderes separat. Og vi har opplæringsprogrammet Dot Product of Vectors og Vector og Mixed Product of Vectors.

Projeksjon av en vektor på en akse

Projeksjonen av vektoren på aksen er lik produktet av lengden til den projiserte vektoren med cosinus til vinkelen mellom vektoren og aksen:

Som du vet, projeksjonen av poenget EN på en rett linje (plan) er bunnen av perpendikulæren droppet fra dette punktet på en rett linje (plan).

La være en vilkårlig vektor (fig. 5), og og være projeksjonene av dens begynnelse (punkter EN) og slutt (punkter B) per akse l... (For å konstruere en projeksjon av et punkt EN) på en rett linje gjennom punktet EN plan vinkelrett på den rette linjen. Skjæringspunktet mellom linjen og planet vil definere den nødvendige projeksjonen.

Vektor komponent på l-aksen kalles en vektor som ligger på denne aksen, hvor begynnelsen sammenfaller med projeksjonen av begynnelsen, og slutten - med projeksjonen av slutten av vektoren.

Projeksjonen av vektoren på aksen l ringte nummeret

,

lik lengden på komponentvektoren på denne aksen, tatt med et plusstegn, hvis retningen til komponentene sammenfaller med aksens retning l, og med et minustegn hvis disse retningene er motsatte.

Grunnleggende egenskaper for vektorprojeksjoner på aksen:

1. Projeksjonene av like vektorer på samme akse er lik hverandre.

2. Når du multipliserer en vektor med et tall, multipliseres dens projeksjon med det samme tallet.

3. Projeksjonen av summen av vektorer på en hvilken som helst akse er lik summen av projeksjonene av summene av vektorene på samme akse.

4. Projeksjonen av vektoren på aksen er lik produktet av lengden til den projiserte vektoren med cosinus til vinkelen mellom vektoren og aksen:

.

Løsning. Projisere vektorer på en akse l som definert i den teoretiske bakgrunnen ovenfor. Det er åpenbart fra fig. 5a at projeksjonen av summen av vektorer er lik summen av projeksjonene av vektorer. Vi beregner disse anslagene:

Finn den endelige projeksjonen av summen av vektorer:

Forholdet mellom en vektor og et rektangulært kartesisk koordinatsystem i rommet

Bekjentskap med et rektangulært kartesisk koordinatsystem i rommet fant sted i den tilsvarende leksjonen, er det ønskelig å åpne den i et nytt vindu.

I et ordnet koordinatsystem 0xyz akser Okse kalt abscisse, akse 0y – y-aksen, og aksen 0z – akseapplikasjon.

Med et vilkårlig poeng M plass vi assosierer vektor

kalt radius vektor poeng M og projisere den på hver av koordinataksene. La oss betegne verdiene til de tilsvarende anslagene:

Tall x, y, z er kalt koordinater til punkt M, henholdsvis abscisse, ordinere og søknad, og er skrevet som en ordnet prikk med tall: M (x; y; z)(fig. 6).

En vektor med lengdeenhet, hvis retning faller sammen med aksens retning, kalles enhetsvektor(eller orthom) aksen. La oss betegne med

Følgelig enhetsvektorene til koordinataksene Okse, Oy, Oz

Teorem. Enhver vektor kan utvides langs enhetsvektorene til koordinataksene:

(2)

Likhet (2) kalles ekspansjonen av vektoren langs koordinataksene. Koeffisientene til denne utvidelsen er projeksjonene av vektoren på koordinataksene. Dermed er ekspansjonskoeffisienten (2) til vektoren langs koordinataksene koordinatene til vektoren.

Etter å ha valgt et bestemt koordinatsystem i rommet, bestemmer vektoren og tripletten av dens koordinater hverandre unikt, slik at vektoren kan skrives i formen

Representasjoner av vektoren i form (2) og (3) er identiske.

Kollinearitetsbetingelse for vektorer i koordinater

Som vi allerede har bemerket, kalles vektorer kollineære hvis de er relatert av relasjonen

La vektorer ... Disse vektorene er kollineære hvis koordinatene til vektorene er relatert av relasjonen

,

det vil si at koordinatene til vektorene er proporsjonale.

Eksempel 6. Gitt vektorer ... Er disse vektorene kollineære?

Løsning. La oss finne ut forholdet mellom koordinatene til disse vektorene:

.

Koordinatene til vektorene er proporsjonale, derfor er vektorene kollineære, eller, som er like, parallelle.

Vektor lengde og retning cosinus

På grunn av den gjensidige perpendikulariteten til koordinataksene, lengden på vektoren

er lik lengden på diagonalen til et rektangulært parallellepiped bygget på vektorer

og kommer til uttrykk ved likheten

(4)

Vektoren er fullstendig definert ved å spesifisere to punkter (start og slutt), så koordinatene til vektoren kan uttrykkes i form av koordinatene til disse punktene.

La, i et gitt koordinatsystem, opprinnelsen til vektoren være ved punktet

og slutten er på punktet

Fra likestilling

Følger det

eller i koordinert form

Derfor, koordinatene til vektoren er lik forskjellene til koordinatene med samme navn på slutten og begynnelsen av vektoren ... Formel (4) i dette tilfellet har formen

Retningen til vektoren bestemmes av retning cosinus ... Dette er cosinusene til vinklene som vektoren danner med aksene Okse, Oy og Oz... La oss betegne disse vinklene α , β og γ ... Da kan cosinusene til disse vinklene bli funnet av formlene

Retningscosinus til en vektor er også koordinatene til enhetsvektoren til denne vektoren og dermed vektorvektoren

.

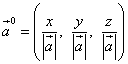
Tatt i betraktning at lengden på vektoren ort er lik en enhet, altså

,

vi oppnår følgende likhet for retningskosinusene:

Eksempel 7. Finn lengden på en vektor x = (3; 0; 4).

Løsning. Lengden på vektoren er

Eksempel 8. Poeng gis:

Finn ut om trekanten bygget på disse punktene er likebenet.

Løsning. Ved å bruke formelen for lengden på vektoren (6), finner vi lengdene på sidene og fastslår om det er to like blant dem:

To like sider ble funnet, derfor er det ikke nødvendig å se etter lengden på den tredje siden, og den gitte trekanten er likebenet.

Eksempel 9. Finn lengden på en vektor og dens retning cosinus hvis .

Løsning. Vektorkoordinater er gitt:

.

Lengden på vektoren er kvadratrot fra summen av kvadratene til koordinatene til vektoren:

.

Finn retningskosinusene:

Løs vektorproblemet selv og se deretter løsningen

Operasjoner på vektorer spesifisert i koordinatform

La det gis to vektorer og gitt ved deres projeksjoner:

La oss indikere handlingene på disse vektorene.

Dato opprettet: 2009-04-11 15:25:51
Sist redigert: 2012-02-08 09:19:45

I lang tid ønsket jeg ikke å skrive denne artikkelen - jeg tenkte på hvordan jeg skulle presentere materialet. Du må også tegne bilder. Men, du skjønner, stjernene har blitt dannet i dag, og det vil være en artikkel om vektorer. Selv om dette bare er et grovt utkast. I fremtiden vil jeg dele denne artikkelen i flere separate - det er nok materiale. Dessuten vil artikkelen gradvis forbedres: Jeg vil gjøre endringer i den. i ett møte vil det ikke være mulig å avsløre alle aspekter.

Vektorer ble introdusert til matematikk på det nittende århundre for å beskrive mengder som var vanskelige å beskrive ved å bruke skalarverdier.

Vektorer brukes mye i utviklingen av dataspill. De brukes ikke bare tradisjonelt - for å beskrive slike mengder som styrke eller hastighet, men også i områder som ikke ser ut til å ha noe med vektorer å gjøre: lagring av farger, skaper skygger.

Skalarer og vektorer

Først, la meg minne deg på hva en skalar er og hvordan den skiller seg fra en vektor.

Skalarverdier lagrer en viss mengde: masse, volum. Det vil si at det er en enhet som er preget av bare ett tall (for eksempel mengden av noe).

En vektor, i motsetning til en skalar, beskrives ved hjelp av to verdier: størrelse og retning.

En viktig forskjell mellom vektorer og koordinater: vektorer er ikke knyttet til et bestemt sted! Nok en gang er det viktigste i en vektor lengde og retning.

En vektor er merket med en fet bokstav i det latinske alfabetet. For eksempel: en, b, v.

I den første figuren kan du se hvordan vektoren er utpekt på planet.

Vektorer i verdensrommet

I verdensrommet kan vektorer uttrykkes ved hjelp av koordinater. Men først må du introdusere ett konsept:

Punktradiusvektor

Ta et punkt M (2,1) i rommet. Radiusvektoren til et punkt er en vektor som starter ved origo og slutter ved punktet.

Vi har ikke noe mer enn en vektor her OM... Vektorstartkoordinater (0,0), sluttkoordinater (2,1). Vi betegner denne vektoren som en.

I dette tilfellet kan vektoren skrives som følger en = <2, 1>... Dette er koordinatformen til vektoren en.

Koordinatene til en vektor kalles dens komponenter i forhold til aksene. For eksempel er 2 en vektorkomponent en om x-aksen.

La oss ta en ny titt på hva punktkoordinater er. Koordinaten til et punkt (for eksempel x) er projeksjonen av et punkt på en akse, dvs. bunnen av perpendikulæren falt fra et punkt på en akse. I vårt eksempel, 2.

Men tilbake til det første bildet. Vi har her to punkter A og B. La koordinatene til punktene være (1,1) og (3,3). Vektor v i dette tilfellet kan betegnes som følger v = <3-1, 3-1>... En vektor som ligger i to punkter i tredimensjonalt rom vil se slik ut:

v =

Jeg tror det ikke er noen vanskeligheter her.

Multiplisere en vektor med en skalar

En vektor kan multipliseres med skalarverdier:

k v = =

Dette multipliserer skalarverdien med hver komponent i vektoren.

Hvis k> 1, vil vektoren øke, hvis k er mindre enn én, men mer enn null, vil vektoren avta i lengde. Hvis k er mindre enn null, vil vektoren endre retning.

Enhetsvektorer

Enhetsvektorer er vektorer hvis lengde er lik én. Legg merke til vektoren med koordinater<1,1,1>vil ikke være lik en! Å finne lengden på vektoren er beskrevet nedenfor i teksten.

Det finnes såkalte enhetsvektorer - dette er enhetsvektorer, som sammenfaller i retning med koordinataksene. Jeg- enhetsvektor for x-aksen, j- enhetsvektor for y-aksen, k er enhetsvektoren til z-aksen.

Hvori Jeg = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

Nå vet vi hva multiplikasjon av en vektor med en skalar er og hva enhetsvektorer er. Nå kan vi skrive v i vektorform.

v= v x Jeg+ v y j+ v z k, hvor v x, v y, v z er de tilsvarende komponentene til vektoren

Vektor tillegg

For å forstå den forrige formelen fullt ut, må du forstå hvordan vektoraddisjon fungerer.

Alt er enkelt her. Ta to vektorer v1 = og v 2 =

v 1 + v 2 =

Vi legger bare til de tilsvarende komponentene til de to vektorene.

Differansen beregnes på samme måte.

Dette er med tanke på den matematiske formen. For fullstendighetens skyld er det verdt å vurdere hvordan addisjon og subtraksjon av vektorer vil se ut grafisk.

For å legge til to vektorer en+b... Du må matche begynnelsen av vektoren b og slutten av vektoren en... Deretter, mellom begynnelsen av vektoren en og slutten av vektoren b tegne en ny vektor. For klarhet, se den andre figuren (bokstaven "a").

For å trekke fra vektorer må du kombinere begynnelsen av to vektorer og tegne en ny vektor fra slutten av den andre vektoren til slutten av den første. Det andre bildet (bokstaven "b") viser hvordan det ser ut.

Vektorlengde og retning

La oss først se på lengden.

Lengde er den numeriske verdien til vektoren, unntatt retning.

Lengden bestemmes av formelen (for en tredimensjonal vektor):

kvadratroten av summen av kvadratene til vektorkomponentene.

En kjent formel, ikke sant? Generelt er dette formelen for lengden på et segment

Retningen til vektoren bestemmes av retningscosinusene til vinklene som dannes mellom vektoren og koordinataksene. For å finne retningskosinusene brukes de tilsvarende komponentene og lengden (bildet kommer senere).

Representerer vektorer i programmer

Det finnes ulike måter å representere vektorer på i programmer. Både ved hjelp av ordinære variabler, som ikke er effektive, og ved hjelp av arrays, klasser og strukturer.

Float vektor3 = (1,2,3); // array for lagring av en vektorstruktur vektor3 // struktur for lagring av vektorer (float x, y, z;);

De største mulighetene for lagring av vektorer er gitt av klasser. I klasser kan vi beskrive ikke bare selve vektoren (variabler), men også vektoroperasjoner (funksjoner).

Punktprodukt av vektorer

Det er to typer vektormultiplikasjon: vektor og skalar.

Et særtrekk ved prikkproduktet er at resultatet alltid vil være en skalarverdi, d.v.s. Nummer.

Her er det verdt å ta hensyn til følgende punkt. Hvis resultatet av denne operasjonen er null, er de to vektorene vinkelrette - vinkelen mellom dem er 90 grader. Hvis resultatet er større enn null, er vinkelen mindre enn 90 grader. Hvis resultatet er mindre enn null, er vinkelen større enn 90 grader.

Denne operasjonen er representert av følgende formel:

en · b= a x * b x + a y * b y + a z * b z

Punktproduktet er summen av produktene til de tilsvarende komponentene til to vektorer. De. Ta x "s av to vektorer, multipliser dem, og legg dem til med produktet av y" s, og så videre.

Vektorprodukt av vektorer

Vektorproduktet av to vektorer vil resultere i en vektor vinkelrett på disse vektorene.

en x b =

Vi vil ikke diskutere denne formelen i detalj ennå. Dessuten er det ganske vanskelig å huske. Vi kommer tilbake til dette punktet etter å ha gjort oss kjent med determinantene.

Vel, for generell utvikling er det nyttig å vite at lengden på den resulterende vektoren er lik arealet til parallellogrammet bygget på vektorer en og b.

Vektornormalisering

En normalisert vektor er en vektor hvis lengde er én.

Formelen for å finne den normaliserte vektoren er som følger - alle komponenter i vektoren må deles på lengden:

v n = v/ | v | =

Etterord

Som du sikkert har sett, er vektorer ikke vanskelige å forstå. Vi har dekket en rekke vektoroperasjoner.

I de neste artiklene i "matematikk"-delen vil vi diskutere matriser, determinanter, systemer lineære ligninger... Alt dette er teori.

Etter det skal vi se på matrisetransformasjoner. Det er da du vil forstå hvor viktig matematikk er for å lage dataspill. Dette emnet vil bare bli en praksis for alle de tidligere emnene.