Kreativt arbeid "påføring av en toppformel". Geometri

Plukke formel

1. Introduksjon

2. Peak formel. Bevis I.

Bevis II.

Bevis sh.

3. Oppgaver.

4. Formelen av polygonområdet gjennom koordinatene til hjørnene.

5. Oppgaver.

6. Litteratur

Peak formel.

1. Introduksjon.

I historien tegner vi visdom,

i poesi - Wit,

i matematikk - innsikt.

F. Bacon.

Tomten vil utfolde seg på det vanlige stykket rutet papir.

Linjene som går på sidene av cellene, danner et rutenett, og cellens hjørner er noder av dette rutenettet. Vi tegner en polygon på arket med hjørner i nodene og finner sitt område.

Du kan søke etter det på forskjellige måter. For eksempel kan du kutte en polygon på ganske enkle figurer, finne dem og brette.

Men her venter vi på mye problemer. Figuren er lett delt inn i rektangler, trapeszoider og trekanter, og området er beregnet uten innsats.

Selv om polygonen ser enkel nok ut, for å beregne sitt område må det være ganske vanskelig. Og hvis en polygon så mer bisarre? Det viser seg at området av polygoner, som er plassert i rutenettet, kan beregnes mye enklere: det er en formel som forbinder dem med antall noder som ligger inne og på grensen til polygonen . Denne fantastiske og enkle formelen kalles en peak formel.

2. Peak formel.

Toppene på polygonen (ikke nødvendigvis konvekse) er plassert i nodene i heltallet gitteret. Innvendig ligger det i rutenettknutene, og i kysten av nodene. Vi bevise at området er lik + - 1 (Peak formel).

Bevis I.

Tenk på en polygon hvis hjørner er i nodene av et heltallsnett, det vil si, ha heltallkoordinater.

Polygonen vil bryte på trekanter med hjørner i gridnoder som ikke inneholder noder enten inne eller på sidene.

Betegne:

n. - Antall parter i polygonen,

m. - Antall trekanter med hjørner i rutenettoder som ikke inneholder noder enten inne eller på sidene,

B - antall noder inne i polygonen,

M er antall noder på sidene, inkludert hjørner.

Området for alle disse trekanter er det samme og lik.

Følgelig er polygonområdet lik
.

180 0 m. .

Finn nå dette beløpet på en annen måte.

Summen av vinklene med et toppunkt i en hvilken som helst intern node er 360 0.

Deretter er summen av vinklene med hjørnene i alle interne noder 360 0 V.

Den totale mengden vinkler ved noder på sidene, men ikke i vertiktene er 180 0 (G - n.).

Summen av vinklene på toppen av polygonen er 180 0 ( n. – 2) .

Den totale mengden av vinklene til alle trekanter er like 360 0 i + 180 0 (g - n.) + 180 0 (n. – 2).

Dermed 180 0 m. \u003d 360 0 i + 180 0 (g - n.) + 180 0 (n. – 2),

180 0 m. \u003d 360 0 i + 180 0 g - 180 0 n. + 180 0 n. - 180 0 · 2,

180 0 m. \u003d 360 0 i + 180 0 g - 360 0,

\u003d B +. – 1 ,

hvor får jeg et uttrykk for et polygon-område:

S.\u003d B +. – 1 ,

kjent som en toppformel.

Figur: B \u003d 24, G \u003d 9, derfor,S. = 24 + – 1 = 27,5.

Finn området av den første polygonen i henhold til Peak-formelen:

B \u003d 28 (grønne prikker);

G \u003d 20 (blå prikker).

Vi får s \u003d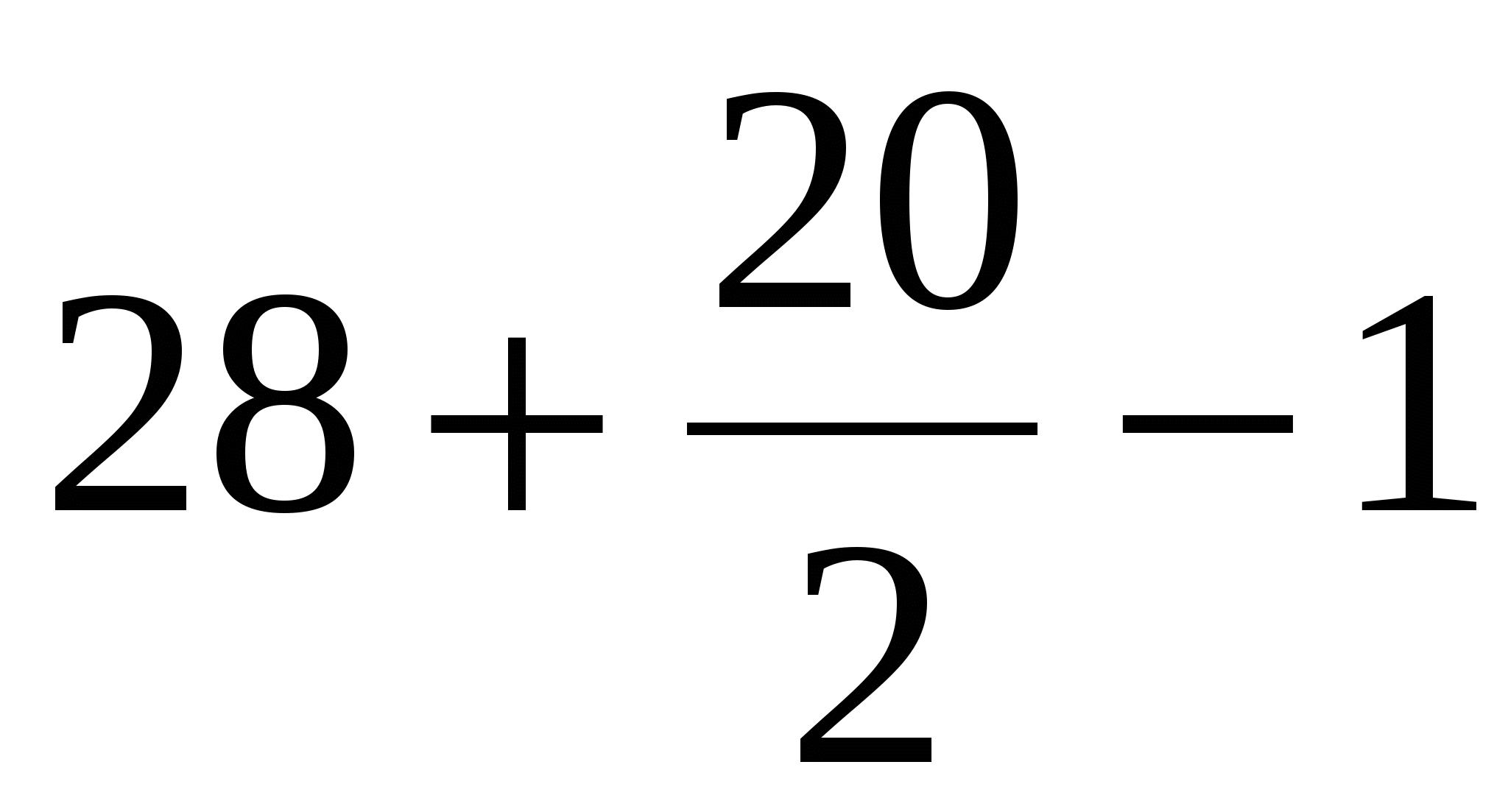
\u003d 37 kvm M.

Bevis II.

Hver polygon m med hjørner i nodene av et heltall gitter som legges i samsvar med nummeret f (m) \u003d
hvor summasjonen utføres på alle rutenettet som tilhører M, og vinkelen Bestemt som følger: =
For det indre punktet i polygonen, =
for et grensepunkt annet enn toppen og - Vinkel øverst, hvis denne noden er et toppunkt. Det er lett å se det f (m) \u003d
+
\u003d B +. - 1. Det gjenstår å verifisere at tallet f (m) er lik området i Polygon M.

La polygonen m bli kuttet i polygoner m 1 og m 2 med hjørner i rutenettet. Deretter f (m) \u003d f (m 1) + f (m 2), for for hver node, er vinklene brettet. Derfor, hvis toppformelen er riktig for to av polygonene M, M 1 og M 2, så er det sant for den tredje.

Hvis m er et rektangel med sidene s og q.rettet langs gitterlinjene

f (m) \u003d (P - 1) (q - 1) +
\u003d PQ.

I dette tilfellet er toppformelen gyldig. Ved å kutte et rektangel M diagonal på trekanter m 1 og m 2 og anvende det faktum at f (m) \u003d f (m 1) + f (m 2) og f (m 1) \u003d f (m 2), er det enkelt For å bevise fairness av toppformelen for enhver rektangulær trekant med tollen rettet langs gitterlinjene. Jeg kuttet av noen slike trekanter fra rektangelet, du kan få noen trekant.

For å fullføre beviset på toppformelen, gjenstår den å legge merke til at noen polygon kan kuttes i trekanter med ikke-kryssende diagonaler.

Bevis sh.

Forholdet mellom formområdet og antall noder som faller inn i denne figuren, er spesielt tydelig synlig i tilfelle et rektangel.

La være Abcd. - Rektangel med hjørner i noder og sider, går langs rutenettlinjene.

Betegne av. Iantallet noder ligger inne i rektangelet, og gjennom G. - Antall noder ved grensen. Flytt rutenettet på gulvet i cellen til høyre og lyet ned.

Deretter kan området av rektangelet "distribuere" mellom noder som følger: hver av Inoder "kontrollerer" en hel celle i det fordrevne grid, hver av G. - 4 grensen ikke-brennende noder - halvparten av cellen, og hver av de vinkelpunktene er en fjerdedel av cellen. Derfor er området av rektangelet S like

Så, for rektangler med hjørner i nodene og partene som går på rutenettlinjene, installerte vi formelen

Vi bevise at denne formelen er sant, ikke bare for rektangler, men også for vilkårlig polygoner med hjørner i rutenettet.

Betegne av. S. m. polygon-områdetM. med hjørner i noder, og gjennomS m. - omfanget
hvorI m. - Antall noder inniM, men G. m. - Antallet noder på grensen. Deretter kan toppformelen skrives som
.

Bevis på formelen for å bryte noen få skritt.

Trinn 1.

Hvis en polygonM. med hjørner i nodene av masken kuttet i 2 polygonerM. 1 og M. 2 , også ha topper bare i rutenettet, da
. La en polygon.M. kutt i polygonerM. 1 og M. 2 med hjørner i noder segmentAv. Alle noder, bortsett fra de som faller på kuttetAB. gi det samme bidraget til venstre og høyre på formelen. Tenk på nodene som ligger på segmentet av AV.

Hvis en slik knute ligger mellom A og IN (for eksempel C), så for en polygonM. det er internt, og for polygonerM. 1 og M. 2 - Border. Så hans bidrag tilS m. lik 1, og i hvert av uttrykkene
og
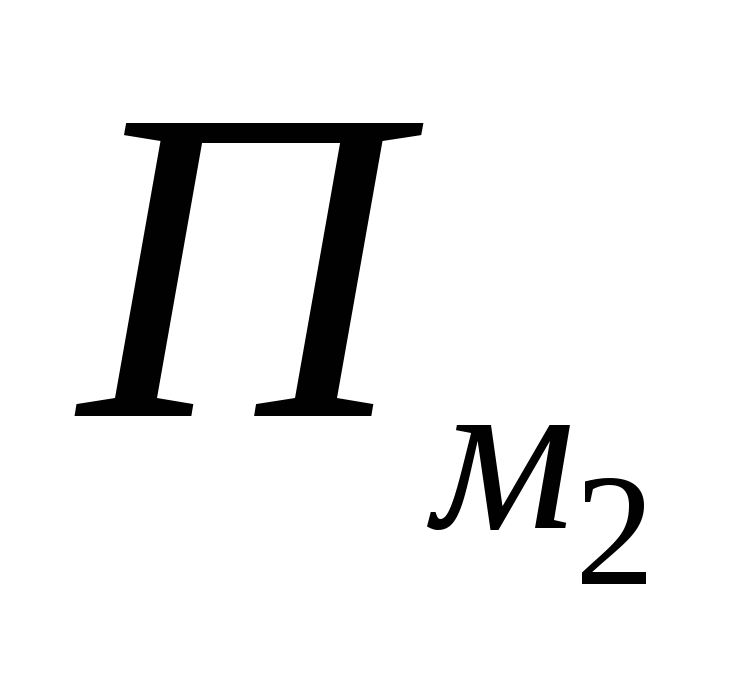- 0,5, det vil si bidragene til denne noden iS m. og
lik.

Tenk på nodene A og V. De er grense som for M.og for M. 1 , M. 2 .

Derfor bidrar bidraget til hver av disse nodene iS m. lik 0,5 og i
- enhet. Så, det totale bidraget til noder A og BS m. lik 1, som er 1 mindre enn deres bidrag til
. Men
, men .

Fra det generelle "bidraget" av alle noder S m. subtraheres 1, og fra
Fjern 2, og dette kompenserer for forskjellen i bidragene til noder A og V.

Så,
.

Steg 2.

Hvis en polygon M.med hjørner i nodene av masken kuttet i to polygoner M. 1 og M. 2 (også med hjørner i noder) og formelen er sant for noen av de to polygonene M, M. 1 , M. 2 , så er det sant for den tredje polygonen.

La for eksempel, det er sant forM. 1 og M. 2 , dvs
. Da (i første trinn), men på første trinn) Det siste uttrykket er likS m. , og likestilling
Og det er en toppformel.

Trinn 3.

Vi beviser Peak-formelen for en rektangulær trekant med hjørner i rutenettverk og kunder som ligger på rutenettlinjene.

Triangel ABC Kaste til rektangel Abcd. .

For rektangler er toppformelen riktig: S. Abcd. \u003d P. Abcd. . Ifølge det første trinnet S Abcd. \u003d P. ABC + P. ACD. , P. ABC \u003d P. ACD. , så det S Abcd. \u003d 2p. ABC . Men S. Abcd. = 2 S. ABC . derfor S. ABC \u003d P. ABC .

Trinn 4.

Peakformelen er riktig for en vilkårlig trekant med hjørner i rutenettet noder.

Etter å ha vurdert tegningen, er det lett å forstå: En slik trekant kan oppnås, "kutte av" fra noe rektangel med sidene som beveger seg langs rutenettlinjene, flere rektangler og rektangulære trekanter med toll på rutenettlinjene. Og siden toppformelen er sant for rektangler og rektangulære trekanter, så (Husk trinn 2) er det sant for den opprinnelige trekanten.

Vi har bevist at hvis en polygon kan kuttes i trekanter med hjørner i rutenettet, er toppformelen sant for det.

3. Oppgaver.

Finn firkantene i figurene:

1
.

B \u003d 9.

R \u003d 4.

B \u003d 9.

R \u003d 5.

1

Hibadullina G.I. (Nurlat, Maou School nr. 1)

1. BoyNyovich E.A., Dorofeyev G.V., Suvorova S.B. og andre. Matematikk. Aritmetikk. Geometri. Grad 5: Pedagogisk. For generell utdanning. organisasjoner med adj. på en elektron. Carrier -3-E Ed. - M.: Opplysning, 2014. - 223, s. : Il. - (sfærer).

2. BoyNyovich E.A., Kuznetsova L.V., Minaeva S.S. og andre. Matematikk. Aritmetikk. Geometri. Grad 6: Utdanning. For generell utdanning. organisasjoner. 5. Ed. - M.: Opplysning, 2016. - 240 C.: IL. - (sfærer).

3. Vasilyev N.B. Rundt formelen i toppen // Kvant. - 1974. - №2. - P. 39-43.

4. ROSETS V.V. Oppgaver for planimetri. 5. Ed., Act. og legg til. - M.: 2006. - 640 p.

5. Yashchenko i.v. Oge. Matematikk: Typiske undersøkelser: O-39 36 Alternativer - M.: Forlagsvirksomhet "National Education", 2017. - 240 s. - (oge. FIPIX - SCHOOL).

6. Jeg dekorerer oge: matematikk. Undervisningssystem Dmitry Gushchina. Oge-2017: Oppgaver, svar, løsninger [elektronisk ressurs]. - Tilgangsmodus: https://oge.sdamgia.ru/test?id\u003d6846966 (Appeldato 04/02/2017).

Jeg er en klasse 6-student. Han begynte å studere geometri siden i fjor, fordi jeg gjør i skolen på læreboken "matematikk. Aritmetikk. Geometri "redigert av E.A. Binaovich, L.V. Kuznetsova, S.S. Minaeva og andre.

Temaene til "kvadratet av figurene" ble tiltrukket størst oppmerksomhet, "kompilering av formler." Jeg la merke til at området av de samme tallene finnes på ulike måter. I hverdagen møter vi ofte oppgavene for å finne området. For eksempel finner du gulvområdet som må male. Merkelig fordi å kjøpe det nødvendige antall tapet for reparasjon, må du vite størrelsen på rommet, dvs. Firkantede vegger. Beregningen av torget på torget, rektangelet og den rektangulære trekanten forårsaket ikke meg vanskeligheter.

Interessert i dette emnet, begynte jeg å se etter et ekstra materiale på internett. Som et resultat av søket kom jeg over toppformelen en formel for å beregne polygonområdet trukket på det rutete papiret. Beregning av området for denne formelen virket for meg tilgjengelig for enhver student. Derfor bestemte jeg meg for å gjennomføre forskningsarbeid.

Relevans av emnet. Dette emnet er et supplement og dypere studiet av geometri kurset.

Studien av dette emnet vil bedre forberede seg på olympiatene og eksamenene.

Formål med arbeidet:

1. Bli kjent med formelen av toppen.

2. Send metodene for beslutninger av geometriske problemer ved hjelp av toppformelen.

3. Systematiser og oppsummer teoretiske og praktiske materialer.

Forskningsoppgaver:

1. Kontroller effektiviteten og muligheten for å bruke formelen når du løser oppgaver.

2. Lær å bruke en toppformel i oppgaver av forskjellig kompleksitet.

3. Sammenlign oppgaver løst ved hjelp av toppformelen og på den tradisjonelle måten.

Hoveddel

Historisk referanse

Georg Alexander Peak - Østerrikske matematikk, født 10. august i året. Han var et begavet barn, faren hans ble lært, ledet av en privat institusjon. På 16, Georg ble uteksaminert fra skolen og kom inn i Universitetet i Wien. I en alder av 20 mottok retten til å undervise fysikk og matematikk. Worldwide Fame brakte en formel for å bestemme området av gitteret i polygonene. Han publiserte sin formel i artikkelen i 1899. Hun ble populær når den polske forskeren Hugo Steinhuz inkluderte den i 1969 i publikasjonen av matematiske skudd.

Georg Peak ble utdannet ved University of Vienna og forsvarte kandidaten i 1880. Etter å ha mottatt doktorgrad, ble han utnevnt til assistent til Ernest Mach i Sher Ferdinanand University i Praha. Han ble også lærer. Han bodde i Praha til sin oppsigelse i 1927, og deretter returnert til Wien.

Peak ble ledet av komiteen i det tyske universitetet i Praha, som utnevnte Einstein av professor i Institutt for matematisk fysikk i 1911.

Han ble valgt medlem av det tsjekkiske vitenskapsakademiet, men ble ekskludert etter å ha fanget nazistene Praha.

Da nazistene kom inn i Østerrike 12. mars 1938, kom han tilbake til Praha. I mars 1939 invaderte nazistene Tsjekkoslovakia. Den 13. juli 1942 ble toppen deportert til Teresyienstadt-leiren skapt av nazistene i National Tsjekkia, hvor han døde to uker senere i en alder av 82 år.

Forskning og bevis

Jeg startet mitt forskningsarbeid med å finne ut spørsmålet: Hvilke figurer kan jeg finne torget? Lag en formel for å beregne området av forskjellige trekanter og quadrangles jeg kunne. Men hva med fem-, seks og generelt med polygoner?

Under studien på ulike steder så jeg løsninger på oppgavene for å beregne området fem-, seks- og andre polygoner. En formel som lar deg løse disse oppgavene, kalt Peak-formelen. Det ser slik ut: S \u003d B + g / 2-1, hvor i antall noder som ligger inne i polygonen, er G-antall noder som ligger på grensen til polygonen. Specularity av denne formelen er at den kun kan brukes til polygoner trukket på det rutete papiret.

Enhver slik polygon er lett å splitte seg i trekanter med topper i grille noder som ikke inneholder noder enten inne eller på sidene. Det kan vises at området av alle disse trekantene er de samme og lik ½, og følgelig er polygonområdet lik halvparten av deres nummer T.

For å finne dette nummeret, betegner n antall parter i polygonen, gjennom antall noder inne i den, gjennom g er antall noder på sidene, inkludert hjørner. Den totale mengden av vinklene til alle trekanter er 180 °. T.

Nå finner vi beløpet på en annen måte.

Summen av vinklene med et toppunkt i en hvilken som helst intern node er 2,180 °, dvs. Den totale mengden av hjørnene er 360 °. I; Den totale mengden vinkler ved noder på sidene, men ikke i vertiktene som er lik (G-N) 180 °, og summen av vinklene ved toppene i polygonen vil være lik (M - 2) 180 °. Således t \u003d 2,180 °. B + (Mr.) 180 ° + (N-2) 180 °. Ved å åpne brakettene og dele 360 \u200b\u200b°, får vi en formel for et polygonområde, kjent som en toppformel.

Praktisk del

Denne formelen bestemte seg for å sjekke oppgavene fra Oge-2017-samlingen. Tok oppgaven med å beregne området av trekanten, quadrangle og Pentagon. Jeg bestemte meg for å sammenligne svarene, løsningen på to måter: 1) Leverte tallene til rektangelet og fra området av rektangelet som ble oppnådd, ble området med rektangulære trekanter trukket. 2) påført toppformelen.

S \u003d 18-1,5-4,5 \u003d 12 og s \u003d 7 + 12 / 2-1 \u003d 12.

S \u003d 24-9-3 \u003d 12 og s \u003d 7 + 12 / 2-1 \u003d 12.

S \u003d 77-7,5-12-4,5-4 \u003d 49 og s \u003d 43 + 14 / 2-1 \u003d 49.

Sammenligning av det oppnådde, konkludere med at begge formler gir det samme svaret. Finn området av figuren i formelen av toppen viste seg å være raskere og enklere, fordi beregningene var mindre. Enkel løsning og spare tid på beregninger vil være nyttig for meg i fremtiden når ANGE er levert.

Det presset meg for å sjekke muligheten for å bruke toppformelen på mer komplekse figurer.

S \u003d 0 + 4/2 -1 \u003d 1

S \u003d 5 + 11 / 2-1 \u003d 9.5

S \u003d 4 + 16 / 2-1 \u003d 1

Konklusjon

Peak-formelen er enkel i forståelse og praktisk å bruke. Først er det nok å bli vurdert å bli vurdert, dele på 2, fold og trekk. For det andre kan du finne et område og en kompleks figur, uten å bruke mye tid på. For det tredje fungerer denne formelen for noen polygon.

Ulempen er at toppformelen gjelder bare for figurer som er trukket på det rutede papiret, og hjørnene ligger på nodene av cellene.

Jeg er sikker på at når man overgir de avsluttende eksamenene, vil oppgavene for beregning av tallene ikke forårsake vanskeligheter. Tross alt er jeg allerede kjent med formelen av topp.

Bibliografisk referanse

Gabbazov N.N. Peak formel // Start i vitenskapen. - 2017. - № 6-1. - s. 130-132;
URL: http://science-start.ru/ru/article/view?id\u003d908 (dato for håndtering: 03/05/2020).

Teksten til arbeidet er plassert uten bilder og formler.
Den fulle versjonen av arbeidet er tilgjengelig i fanen "Arbeidsfiler" i PDF-format

Introduksjon

Jeg, student klasse 6. Han begynte å studere geometri siden i fjor, fordi jeg gjør i skolen på læreboken "matematikk. Aritmetikk. Geometri "redigert av E.A. Binaovich, L.V. Kuznetsova, S.S. Minaeva og andre.

Temaene til "kvadratet av figurene" ble tiltrukket størst oppmerksomhet, "kompilering av formler." Jeg la merke til at området av de samme tallene finnes på ulike måter. I hverdagen møter vi ofte oppgavene for å finne området. For eksempel finner du gulvområdet som må male. Merkelig fordi å kjøpe det nødvendige antall tapet for reparasjon, må du vite størrelsen på rommet, dvs. Firkantede vegger. Beregningen av torget på torget, rektangelet og den rektangulære trekanten forårsaket ikke meg vanskeligheter.

Interessert i dette emnet, begynte jeg å se etter et ekstra materiale på internett. Som et resultat av søket kom jeg over toppformelen en formel for å beregne polygonområdet trukket på det rutete papiret. Beregning av området for denne formelen virket for meg tilgjengelig for enhver student. Derfor bestemte jeg meg for å gjennomføre forskningsarbeid.

Relevans av emnet:

Dette emnet er et supplement og dypere studiet av geometri kurset.

Studien av dette emnet vil bedre forberede seg på olympiatene og eksamenene.

Formål med arbeidet:

Bli kjent med formelen av toppen.

Send teknikkene for geometriske oppgaver ved hjelp av toppformelen.

Systematisere og oppsummere teoretiske og praktiske materialer.

Forskningsoppgaver:

Kontroller effektiviteten og muligheten for å bruke formelen når du løser oppgaver.

Lær å bruke en toppformel i oppgaver av forskjellig kompleksitet.

Sammenlign oppgaver løst ved hjelp av toppformelen og på den tradisjonelle måten.

Hoveddel

1.1. Historisk referanse

Georg Alexander Peak - Østerrikske matematiker, ble født 10. august 1859. Han var et begavet barn, faren hans ble lært, ledet av en privat institusjon. På 16, Georg ble uteksaminert fra skolen og kom inn i Universitetet i Wien. I en alder av 20 mottok retten til å undervise fysikk og matematikk. Worldwide Fame brakte en formel for å bestemme området av gitteret i polygonene. Han publiserte sin formel i artikkelen i 1899. Hun ble populær når den polske forskeren Hugo Steinhuz inkluderte den i 1969 i publikasjonen av matematiske skudd.

Georg Peak ble utdannet ved University of Vienna og forsvarte kandidaten i 1880. Etter å ha mottatt doktorgrad, ble han utnevnt til assistent til Ernest Mach i Sher Ferdinanand University i Praha. Han ble også lærer. Han bodde i Praha til sin oppsigelse i 1927, og deretter returnert til Wien.

Peak ble ledet av komiteen i det tyske universitetet i Praha, som utnevnte Einstein av professor i Institutt for matematisk fysikk i 1911.

Han ble valgt medlem av det tsjekkiske vitenskapsakademiet, men ble ekskludert etter å ha fanget nazistene Praha.

Da nazistene kom inn i Østerrike 12. mars 1938, kom han tilbake til Praha. I mars 1939 invaderte nazistene Tsjekkoslovakia. Den 13. juli 1942 ble toppen deportert til Teresyienstadt-leiren skapt av nazistene i National Tsjekkia, hvor han døde to uker senere i en alder av 82 år.

1.2. Forskning og bevis

Jeg startet mitt forskningsarbeid med å finne ut spørsmålet: Hvilke figurer kan jeg finne torget? Lag en formel for å beregne området av forskjellige trekanter og quadrangles jeg kunne. Men hva med fem-, seks og generelt med polygoner?

Under studien på ulike steder så jeg løsninger på oppgavene for å beregne området fem-, seks- og andre polygoner. En formel som lar deg løse disse oppgavene, kalt Peak-formelen. Hun ser slik ut: S \u003d B + g / 2-1hvor I - Antallet noder ligger inne i polygonen, G.- Antallet noder som ligger på grensen til polygonen. Specularity av denne formelen er at den kun kan brukes til polygoner trukket på det rutete papiret.

Enhver slik polygon er lett å splitte seg i trekanter med topper i grille noder som ikke inneholder noder enten inne eller på sidene. Det kan vises at området av alle disse trekantene er de samme og lik ½, og følgelig er polygonområdet lik halvparten av nummeret deres T.

Å finne dette nummeret, betegne av n antall parter i polygonen, gjennom I- Antallet noder inne i det, gjennom G.- Antallet noder på sidene, inkludert hjørner. Den totale mengden av vinklene til alle trekanter er 180 °. T.

Nå finner vi beløpet på en annen måte.

Summen av vinklene med et toppunkt i en hvilken som helst intern node er 2,180 °, dvs. Den totale mengden av hjørnene er 360 °. I;den totale mengden vinkler ved noder på sidene, men ikke på hjørnene er lik ( G- n) 180°, og summen av hjørnene på toppen av polygonen vil være lik ( G- 2) 180°. På denne måten, T \u003d.2.180 °. B + (Mr.) 180° + (n -2)180 °. Ved å åpne brakettene og dele 360 \u200b\u200b°, får vi en formel for et polygonområde, kjent som en toppformel.

2. Praktisk del

Denne formelen bestemte seg for å sjekke oppgavene fra Oge-2017-samlingen. Tok oppgaven med å beregne området av trekanten, quadrangle og Pentagon. Jeg bestemte meg for å sammenligne svarene, løsningen på to måter: 1) Leverte tallene til rektangelet og fra området av rektangelet som ble oppnådd, ble området med rektangulære trekanter trukket. 2) påført toppformelen.

S \u003d 18-1,5-4,5 \u003d 12 og s \u003d 7 + 12 / 2-1 \u003d 12

S \u003d 24-9-3 \u003d 12 og s \u003d 7 + 12 / 2-1 \u003d 12

S \u003d 77-7,5-12-4,5-4 \u003d 49 og s \u003d 43 + 14 / 2-1 \u003d 49

Sammenligning av det oppnådde, konkludere med at begge formler gir det samme svaret. Finn området av figuren i formelen av toppen viste seg å være raskere og enklere, fordi beregningene var mindre. Enkel løsning og spare tid på beregninger vil være nyttig for meg i fremtiden når ANGE er levert.

Det presset meg for å sjekke muligheten for å bruke toppformelen på mer komplekse figurer.

S \u003d 0 + 4/2 -1 \u003d 1

S \u003d 5 + 11 / 2-1 \u003d 9.5

S \u003d 4 + 16 / 2-1 \u003d 1

Konklusjon

Peak-formelen er enkel i forståelse og praktisk å bruke. Først er det nok å bli vurdert å bli vurdert, dele på 2, fold og trekk. For det andre kan du finne et område og en kompleks figur, uten å bruke mye tid på. For det tredje fungerer denne formelen for noen polygon.

Ulempen er at toppformelen gjelder bare for figurer som er trukket på det rutede papiret, og hjørnene ligger på nodene av cellene.

Jeg er sikker på at når man overgir de avsluttende eksamenene, vil oppgavene for beregning av tallene ikke forårsake vanskeligheter. Tross alt er jeg allerede kjent med formelen av topp.

Bibliografi

Binaovich E.A., Dorofeyev G.V., Suvorova S.B. og andre. Matematikk. Aritmetikk. Geometri. Grad 5: Pedagogisk. For generell utdanning. organisasjoner med adj. på en elektron. Carrier -3-E Ed.-m.: Opplysning, 2014.- 223, s. : Il. - (sfærer).

Baynovich E.A., Kuznetsova L.V., Minaeva S.S. og andre. Matematikk. Aritmetikk. Geometri. Grad 6: Utdanning. For generell utdanning. Organisasjoner - 5. Ed.-M.: Opplysning, 2016.-240C. : IL.- (sfærer).

Vasilyev n.b. Rundt formelen av toppen. //Kvant. - 1974.-№2. -C.39-43.

Rosets v.v. Oppgaver for planimetri. / 5- Ed., Act. Og legg til. - M.: 2006.-640C.

I.v. Yashchenko. Matematikk: Typiske eksamensalternativer: O-39 36 Alternativer - M.: Forlagsvirksomhet "National Education", 2017. -240 s. - (oge. Phi-School).

"Jeg løste oge": matematikk. Undervisningssystem Dmitry Gushchina. Oge-2017: Oppgaver, svar, løsninger [elektronisk ressurs]. Tilgangsmodus: https://oge.sdamgia.ru/test?id\u003d6846966 (Appeldato 04/02/2017)

Tegn litt polygon på det rutete papiret. For eksempel, slik som vist i figur 1.

La oss prøve å beregne sitt område. Hvordan gjøre det? Sannsynligvis det enkleste å bryte den på rektangulære trekanter Og rektangler hvis områder allerede er enkle å beregne og brette resultatene som er oppnådd. Brukes av meg er enkel, men veldig tungvint, i tillegg er det ikke egnet for noen polygoner.

Tenk på et nondegenerert enkelt heltallpolygon (dvs. det er forbundet - noen to punkter kan kobles med en kontinuerlig kurve, helt i den er inneholdt, og alle dens hjørner har hele koordinater, grensen er en sammenhengende brutt uten selvkryssing, og det har et ikke-nullområde). For å beregne området av en slik polygon, kan du bruke følgende theorem:

Peak theorem. La - antall heltallpoeng i polygonen - antall heltallpoeng på grensen - dets område. Så gyldig plukke formel:

Eksempel. For en polygon i figur 1 (gule prikker), (blå prikker, ikke glem om hjørnene!), Derfor, firkantede enheter.

Bevis på topp theorem. Først merker vi at toppformelen er gyldig for en enkelt firkant. Faktisk, i dette tilfellet har vi og

Tenk på et rektangel med sidene som ligger på gitterlinjene. La lengden på sidene hans er like og. Vi har i dette tilfellet i henhold til toppformelen,

Vi vurderer nå en rektangulær trekant med kunder som ligger på koordinataksene. En slik trekant oppnås fra et rektangel med partene og, vurdert i det foregående tilfelle, kutte den på diagonalen. La diagonalene ligge heltallpoeng. Så for denne anledningen, og vi får det

Nå vurdere en vilkårlig trekant. Det kan oppnås ved å kutte av flere rektangulære rektangler fra rektangelet og muligens et rektangel (se figur 2 og 3). Siden både for et rektangel, og for en rektangulær trekant av toppformelen, får vi at det også vil være gyldig for en vilkårlig trekant.

Det gjenstår å gjøre det siste trinnet: gå fra trekanter til polygoner. Eventuelle polygoner kan deles inn i trekanter (for eksempel diagonaler). Derfor er det nødvendig å bare bevise at når det ved å legge til en trekant til en vilkårlig polygon, forblir toppformelen sant.

La polygonen og trekanten ha en vanlig side. Anta at for toppformelen vil vi bevise at det vil være riktig for en polygon oppnådd fra tilsetningen. Siden de har den generelle siden, blir alle heltallpunkter som ligger på denne siden, bortsett fra to hjørner, blir interne punkter i den nye polygonen. Verkene vil være grensepunkter. Betegne antall vanlige poeng gjennom og få

Antallet av interne heltallpunkter i den nye polygonen,

Antall grensepunkter i den nye polygonen.

Fra disse likhetene får vi

Siden vi foreslo at teoremet er sant for og for separat,

Således er toppformelen bevist.

Denne formelen ble åpnet av østerrikske matematikk Peak Georg Alexandrov (1859 - 1943) i 1899. I tillegg til denne formelen åpnet Georg Peak Peak Theorem, Peak - Julia, Peak - Nevalin, viste seg å være ulikhet i Schwartz - Peak. I Vedlegg 1. Du kan se de ikke-standardlige oppgavene som vurderes av meg for å bruke toppformelen.

Plukke formel

Sazhina Valery Andreevna, student 9 Class Maou "Sosh№11" G Ust-Ilimsk Irkutsk Region

Leder: Gubar Oksana Mikhailovna, Matematikklærer av den høyeste kvalifiserende kategorien Mou "Sosh№11" Mr. Ust-Ilimsk Irkutsk Region

2016 år

Introduksjon

Når jeg studerer emnet i geometrien til "Polygon Square", bestemte jeg meg for å finne ut: Er det en måte å finne firkanter på annen måte enn de som vi studerte i leksjonene?

På denne måten er det en toppformel. L. V. Gorina i "Materialer for å finne selvutdanning" beskrevet denne formelen: "Introduksjon til toppformelen er spesielt relevant på Eva av levering av bruk og GIA. Med denne formelen kan du enkelt løse en stor klasse av oppgaver som tilbys på eksamenene - dette er oppgaver å finne området av polygonen som er avbildet på det rutete papiret. Little Peak formel vil erstatte et helt sett med formler som er nødvendige for å løse slike oppgaver. Formelen av toppen vil fungere "en for alle ..."! ".

I eksamensmaterialene møtte jeg oppgavene med det praktiske innholdet i tomter. Jeg bestemte meg for å sjekke om denne formelen gjelder for å finne området i skoleområdet, byens nabolag, område. Så vel som bruken er rasjonelt å løse problemer.

Studieobjekt: Peak formel.

Forskningsfag: Rationalitetsapplikasjon av toppformelen når du løser oppgaver.

Målet med arbeidet er å underbygge rationaliteten til å bruke toppformelen når man løser oppgavene for å finne feltet av tall som er avbildet på det rutete papiret.

Forskningsmetoder: Modellering, sammenligning, generalisering, analogier, studie av litterære og internettressurser, analyse og klassifisering av informasjon.

Plukk opp den nødvendige litteraturen, analysere og systematisere informasjonen som er oppnådd;

Vurder ulike metoder og teknikker for å løse problemer på cellulært papir;

Kontroller eksperimentelt ved rasjonalitet for å bruke toppformelen;

Vurder bruk av denne formelen.

Hypotese: Hvis du bruker toppformelen for å finne området i polygonen, kan du finne området på territoriet, og oppløsningen av oppgaver på det rutete papiret vil være mer rasjonelt.

Hoveddel

Teoretisk del

Rutet papir (mer presist - dets noder) som vi ofte foretrekker å tegne og tegne, er et av de viktigste eksemplene på punktgitteret på flyet. Allerede denne enkle gitteret serverte K. Gauss ved utgangspunktet for å sammenligne området av sirkelen med antall poeng med heltallkoordinater i den. Det faktum at noen enkle geometriske uttalelser om tallene på flyet har dype konsekvenser i aritmetiske studier, ble eksplisitt lagt merke til av byen Minkowski i 1896, da han for første gang for behandling av teoretiske og numeriske problemer tiltrukket geometriske metoder.

Tegn litt polygon på det rutete papiret (Vedlegg 1, Figur 1). La oss prøve å beregne sitt område. Hvordan gjøre det? Sannsynligvis, den enkleste måten å bryte den på rektangulære trekanter og et trapesium, hvis område allerede er lett å beregne og brette resultatene som er oppnådd.

Metoden som brukes er enkel, men veldig tungvint, i tillegg er den ikke egnet for noen polygoner. Så det neste polygon kan ikke brytes ned på rektangulære trekanter, da vi gjorde det i forrige tilfelle (vedlegg 2, figur 2). Du kan for eksempel prøve å legge det til det "gode" som trengs for oss, det vil si området som vi vil kunne beregne den beskrevne metoden, deretter fra det resulterende antallet av området av lagt til del.

Det viser seg imidlertid at det er en veldig enkel formel som gjør at du kan beregne området av slike polygoner med hjørner i noder av torget.

Denne formelen ble åpnet av østerrikske matematikk Peak Georg Alexandrov (1859 - 1943) i 1899. I tillegg til denne formelen åpnet Georg Peak Peak Theorem, Peak - Julia, Peak - Nevalin, viste seg å være ulikhet i Schwartz - Peak.

Denne formelen forblir ubemerket i noen tid etter at toppen publiserte det, men i 1949 inkluderte den polske matematikeren av Hugo-stengauser teoremet i sitt berømte "matematiske kaleidoscope". Fra denne tiden har Peak Theorem blitt allment kjent. I Tyskland er PEAK-formelen inkludert i skole lærebøker.

Det er et klassisk resultat av kombinatorisk geometri og geometri av tall.

Bevis på formelen av toppen

La absd være et rektangel med hjørner i nodene og partene som kjører langs rutenettlinjene (vedlegg 3, figur 3).

Betegne b - antall noder som ligger inne i rektangelet, og gjennom g er antall noder ved grensen. Flytt rutenettet på polene til høyre og lyet

ned. Deretter kan området av rektangelet bli "fordelt" mellom nodene som følger: Hver av nodene "styrer" hele cellen i det fordrevne grid, og hver av nodene - 4 grensen ikke-vinkelknude - halvparten av Cell, og hver av de vinkelpunktene er en fjerdedel av celler. Derfor er området av rektangelet S like

S. \u003d B +. + 4 · \u003d B +. - 1 .

Så, for rektangler med hjørner i nodene og partiene som går på rutenettlinjene, setter vi formelen S \u003d B + - 1 . Dette er en toppformel.

Det viser seg at denne formelen er sant, ikke bare for rektangler, men også for vilkårlig polygoner med hjørner i rutenettet.

Praktisk del

Finne arealet av figurer av en geometrisk metode og av toppformel

Jeg bestemte meg for å sørge for at toppformelen er sant for alle de vurderte eksemplene.

Det viser seg at hvis en polygon kan kuttes i trekanter med hjørner i rutenettet, så er det sant for det peakformelen.

Jeg så på noen utfordringer på cellulært papir med celler på 1 cm1 cm og brukt komparativ analyse Ved å løse oppgaver (tabell nr. 1).

Tabell # 1 Løse oppgaver på ulike måter.

Bilde

Ifølge geometriformelen

Av Peak formel

Oppgave nummer 1

S \u003d S. etc - (2s. 1 + 2s. 2 )

S. etc =4*5=20 cm. 2

S. 1 =(2*1)/2=1 cm. 2

S. 2 =(2*4)/2=4 cm. 2

S \u003d 20- (2 * 1 + 2 * 4) \u003d 10cm. 2

Svar :10 cm. ².

B \u003d 8, R \u003d 6

S. \u003d 8 + 6/2 - 1 \u003d 10 (cm²)

Svar: 10 cm².

Oppgave nummer 2.

a \u003d 2, H \u003d 4

S \u003d a * h \u003d 2 * 4 \u003d 8cm. 2

Svar : 8 cm. ².

B \u003d 6, r \u003d 6

S. \u003d 6 + 6/2 - 1 \u003d 8 (cm²)

Svar: 8 cm².

Oppgave nummer 3.

S \u003d S. kv. - (S. 1 + 2s. 2 )

S. kv. =4 2 =16 cm. 2

S. 1 \u003d (3 * 3) / 2 \u003d 4,5 cm 2

S. 2 \u003d (1 * 4) / 2 \u003d 2cm 2

S.\u003d 16- (4,5 + 2 * 2) \u003d 7,5 cm 2

B \u003d 6, g \u003d 5

S. \u003d 6 + 5/2 - 1 \u003d 7,5 (cm²)

Svar: 7,5 cm².

Oppgave nummer 4.

S \u003d S. etc - (S. 1 + S. 2+ S. 3 )

S. etc =4 * 3=12 cm. 2

S. 1 =(3*1)/2=1,5 cm. 2

S. 2 =(1*2)/2=1 cm. 2

S. 3 =(1+3)*1/2=2 cm. 2

S \u003d 12- (1,5 + 1 + 2) \u003d 7,5cm. 2

B \u003d 5, g \u003d 7

S. \u003d 5 + 7/2 - 1 \u003d 7,5 (cm²)

Svar: 7,5 cm².

Oppgave nummer 5.

S \u003d S. etc - (S. 1 + S. 2+ S. 3 )

S. etc =6 * 5=30 cm. 2

S. 1 =(2*5)/2=5 cm. 2

S. 2 =(1*6)/2=3 cm. 2

S. 3 =(4*4)/2=8 cm. 2

S \u003d 30- (5 + 3 + 8) \u003d 14cm. 2

Svar: 14 cm²

B \u003d 12, r \u003d 6

S. \u003d 12 + 6/2 - 1 \u003d 14 (cm²)

Svar: 14 cm²

En oppgave №6.

S. Tr \u003d (4 + 9) / 2 * 3 \u003d 19,5 cm 2

Svar: 19.5 cm 2

B \u003d 12, g \u003d 17

S. \u003d 12 + 17/2 - 1 \u003d 19.5 (cm²)

Svar: 19.5 cm 2

En oppgave №7. Finn området av skogsmassen (i m²) avbildet på planen med en firkantet mesh 1 × 1 (cm) på en skala på 1 cm - 200 m

S \u003d S. 1 + S. 2+ S. 3

S. 1 =(800*200)/2=80000 m. 2

S. 2 =(200*600)/2=60000 m. 2

S. 3 =(800+600)/2*400=

280000 m. 2

S \u003d.80000+60000+240000=

420000m 2.

Svar: 420.000 m²

B \u003d 8, g \u003d 7. S. \u003d 8 + 7/2 - 1 \u003d 10,5 (cm²)

1 cm² - 200² m²; S. \u003d 40000 · 10.5 \u003d 420 000 (m²)

Svar: 420.000 m²

Oppgave nummer 8. . Finn feltområdet (i m²) avbildet på planen med en firkantet mesh 1 × 1 (cm) på skalaen

1 cm - 200 m.

S.= S. KV -2 ( S. Tr +. S. stige)

S. KV \u003d 800 * 800 \u003d 640000 m 2

S. Tr \u003d (200 * 600) / 2 \u003d 60000m 2

S. Felle \u003d (200 + 800) / 2 * 200 \u003d

100000m 2.

S.=640000-2(60000+10000)=

320000 m 2.

Svar: 320 000 m²

Beslutning. Finne S. Området på quadricle avbildet på den rutete papiret av Peak Formula:S. \u003d B + - 1

B \u003d 7, g \u003d 4. S. \u003d 7 + 4/2 - 1 \u003d 8 (cm²)

1 cm² - 200² m²; S. \u003d 40000 · 8 \u003d 320 000 (m²)

Svar: 320 000 m²

Oppgave nummer 9. . Finn Square.S. sektorer, teller firkantede celler lik 1. Som svar, spesifiserer .

Sektoren er en fjerdedel del av sirkelen, og derfor er området lik et fjerdedel av sirkelen. Sirkelområdet er lik πR. 2 hvor R. - Sirkelradius. I vårt tilfelleR. =√5 Og derfor områdetS. sektorer er 5π / 4. FraS./ π \u003d 1,25.

Svar. 1,25.

R \u003d 5, b \u003d 2, S. \u003d B + g / 2 - 1 \u003d 2 + 5/2 - 1 \u003d 3,5, ≈ 1,11

Svar. 1,11.

Oppgave nummer 10. Finn Square. S. ringer, teller firkantet celler lik 1. Som svar, spesifiserer .

Ringene området er lik forskjellen i området av eksterne og indre sirkler. RadiusR. utvendig sirkel likeverdig

2, radius r. den indre sirkelen er 2. Følgelig er ringområdet 4 Og derfor, . Svar: 4.

R \u003d 8, b \u003d 8, S. \u003d B + g / 2 - 1 \u003d 8 + 8/2 - 1 \u003d 11, ≈ 3,5

Svar: 3.5.

Konklusjoner: De vurderte oppgavene ligner oppgaven fra opsjonene for måling av materialer i eksamen i matematikk (oppgaver nr. 5.6).

Fra de vurderte oppgavebeslutningen, så jeg at noen av dem, som oppgaver nr. 2.6, er det lettere å løse, bruke geometriske formler, siden høyden og basen kan defineres i figuren. Men de fleste oppgavene krever en splitting av figuren til et enklere (oppgavenummer 7) eller fullfører til et rektangel (oppgaver nr. 14,5), en firkant (oppgaver nr. 3,8).

Fra å løse problemer nr. 9 og nr. 10, så jeg at bruken av en toppformel for figurer som ikke er polygoner, gir et omtrentlig resultat.

For å teste rationaliteten til anvendelsen av toppformelen, gjennomførte jeg en studie for tidspunktet (Vedlegg 4, Tabell nr. 2).

Konklusjon: Fra tabellen og diagrammet (Vedlegg 4, Figur 1) Det kan ses at når man løser problemer med formelen i toppen, blir tiden brukt mye mindre.

Finne området av de romlige former

Kontroller anvendelighet av denne formelen til romlige former (Vedlegg 5, Figur 4).

Finn området av den fullstendige overflaten av den rektangulære parallellepipede, teller siden av firkantede celler lik 1.

Dette er mangel på formel.

Anvendelse av toppformelen for å finne området på territoriet

Løse oppgaver med praktisk innhold (oppgaver nummer 7.8; Tabell nr. 1), jeg bestemte meg for å bruke denne metoden for å finne området på skolens territorium, nabolagene i byen Ust-Ilimsk, Irkutsk-regionen.

Etter å ha lest "Prosjektet av grensene til landplottet Mausosh№11 G. Nast-Ilimsk" (Vedlegg 6), fant jeg området på skolens territorium og sammenlignet med et område med landplotgrenser (vedlegg 9 , Tabell 3).

Etter å ha vurdert den rette bredden av Ust-Ilimsk (Vedlegg 7), beregnet jeg MicroDistricon-området og sammenlignet med dataene fra "Ust-Ilimsk" i Irkutsk-regionen. Resultatene som presenteres i tabellen (Vedlegg 9, Tabell 4).

Etter å ha vurdert kartet over Irkutsk-regionen (Vedlegg 7), fant jeg området på territoriet og sammenlignet med dataene fra Wikipedia. Resultatene som presenteres i tabellen (Vedlegg 9, Tabell 5).

Etter å ha analysert resultatene, kom jeg til konklusjonen: Ifølge toppformelen, kan disse områdene bli funnet mye enklere, men resultatene er omtrentlige.

Fra studiene utført, den mest nøyaktige betydningen jeg mottok når jeg finner området på skolens territorium (Vedlegg 10, Figur 2). En større uoverensstemmelse i resultatene lyktes når torget i Irkutsk-regionen (vedlegg 10, figur 3). Dette skyldes det faktum. At ikke alle grensene i regionen er partene i polygonene, og hjørnene er ikke nodale poeng.

Konklusjon

Som et resultat av arbeidet mitt, utvidet jeg min kunnskap om å løse problemer på det rutede papiret, bestemt klassifiseringen av oppgavene som ble studiet.

Når du utfører arbeidet, ble oppgavene løst for å finne området av polygoner som er avbildet på det rutede papiret på to måter: geometrisk og bruk av toppformelen.

Analyse av løsninger og eksperimenter for å bestemme tidspunktet viste at anvendelsen av formelen gjør det mulig å løse oppgaven med å finne området av polygonen, mer rasjonelt. Dette sparer tid til eksamen i matematikk.

Å finne området av forskjellige figurer som er avbildet på det rutete papiret, gjorde det mulig å konkludere med at bruken av en toppformel for beregning av området av den sirkulære sektoren og ringen er upraktisk, da det gir et omtrentlig resultat, og det Peak-formelen gjelder ikke for å løse problemer i rommet.

Også i arbeidet ble det funnet områder av ulike territorier av Peak formel. Det kan konkluderes: bruken av formelen for å finne området av ulike territorier er mulig, men resultatene er omtrentlige.

Hypotesen nominert av meg ble bekreftet.

Jeg kom til den konklusjon at emnet som interesserer meg, er ganske mangesidig, oppgavene på det rutede papiret er forskjellige, metodene og teknikkene til deres beslutninger er også forskjellige. Derfor bestemte jeg meg for å fortsette å jobbe i denne retningen.

Litteratur

VOLKOV S.D .. Prosjekt av grensene til landplottet, 2008, s. seksten.

Gorina L.V., Matematikk. Alt for læreren, M: Science, 2013 g. Nr. 3, s. 28.

Prokopieva v.p., Petrov A.G., generell plan for byen Ust-Ilimsk, Irkutsk-regionen, Gosstroy Russland, 2004. Med. 65.

Riss E. A., Zharkovskaya N. M., Geometri av det rutede papiret. Peak formel. - Moskva, 2009, № 17, s. 24-25.

Smirnova I. M. ,. Smirnov V. A, geometri på cellulært papir. - Moskva, rene dammer, 2009, s. 120.

Smirnova I. M., Smirnov V. A., Geometriske oppgaver med praktisk innhold. - Moskva, rene dammer, 2010, s. 150.

Mål for de åpne bankoppgavene i matematikk FIPI, 2015.

Bykart over Ust-ilimsk.

Kart over Irkutsk-regionen.

Wikipedia.