Сызықтармен шектелген қисық трапеция ауданының формуласы. Қисық сызықты трапеция

№___ Күні________

Тақырыбы:Қисық сызықты трапеция және оның ауданы б

Сабақтың мақсаттары: Анықтамалар беріңіз қисық трапецияжәне оның ауданы, қисық трапеция ауданын есептеуді үйрену.

САБАҚТЫҢ БАРЛЫҒЫ

1. Ұйымдастыру кезеңі.

Оқушылармен амандасу, сыныптың сабаққа дайындығын тексеру, оқушылардың зейінін ұйымдастыру, сабақтың жалпы мақсаты мен жоспарын ашу.

2. Үй тапсырмасын тексеру кезеңі.

Міндеттері: Барлық оқушылардың үй тапсырмасын орындауының дұрыстығын, толықтығын және хабардарлығын анықтау, оқушылардың біліміндегі кемшіліктерді және іс-әрекет әдістерін анықтау. Қиындықтардың себептерін анықтаңыз және табылған олқылықтарды жойыңыз.

3. Жаңарту кезеңі.

Міндеттері: мектеп оқушыларының оқу мотивациясын қамтамасыз ету, сабақтың мақсатын анықтау үшін бірлескен іс-әрекетке қосу. Оқушылардың субъективті тәжірибесін жаңарту.

Негізгі ұғымдар мен формулаларды еске түсірейік.

Анықтама.Функция у=f(x), x (а,б),функцияның антитуындысы деп аталады y=f(x), x (а,б),егер барлығы үшін x (а,б)теңдік сақталады

Ф (x)=f(x).

Пікір.Егер f(x)функцияның антитуындысы бар f(x), содан кейін кез келген тұрақты үшін МЕН, F(x)+Cүшін де антидериватив болып табылады f(x).

Барлығын табу міндеті антитуынды функциялар f(x)интегралдау деп аталады, ал барлық қарсы туындылар жиыны функция үшін анықталмаған интеграл деп аталады. f(x)Авторы dxжәне тағайындалады

Келесі қасиеттер орын алады:

1 . ;

2 . Егер C= Const, онда
;

3 .
.

Пікір.Мектептегі математика курстарында «анықталмаған интеграл» термині қолданылмайды, олар «барлық антитуындылар жиынтығы» дейді.

Мұнда анықталмаған интегралдар кестесі берілген.

1-мысал.Функцияның қарсы туындысын табыңыз
, нүктесі арқылы өту М(2;4).

Шешім.Функцияның барлық антитуындыларының жиыны
анықталмаған интеграл бар
. Оны 1 және 2 интегралының қасиеттерін пайдаланып есептейік. Бізде бар:

Барлық антитуындылардың жиыны функциялар тобымен берілетінін анықтадық y=F(x)+C, яғни y=x 3 – 2x+C, Қайда МЕН– ерікті тұрақты.

Қарсы туындының нүкте арқылы өтетінін білу М(2;4), оның координаталарын алдыңғы өрнектің орнына қойып, табыңыз МЕН.

4=2 3 –2 2+МЕН  МЕН=4–8+4; МЕН=0.

Жауап: F(x)=x 3 - 2x- қажетті антитуынды.

4. Жаңа ұғымдар мен іс-әрекет тәсілдерін қалыптастыру.

Міндеттері: Оқушылардың өтілетін материалды қабылдауын, түсінуін және есте сақтауын қамтамасыз ету. Оқушылардың оқытылатын материалды жаңғырту әдістерін меңгеруін қамтамасыз ету, меңгерілетін ұғымдарды, заңдарды, ережелерді және формулаларды философиялық тұрғыдан түсінуге ықпал ету. Оқушылардың оқытылатын материалдың дұрыстығы мен түсінігін анықтау, алғашқы түсініктегі олқылықтарды анықтау, түзетулер енгізу. Оқушылардың өздерінің субъективті тәжірибесін белгілермен байланыстыруын қамтамасыз етіңіз ғылыми білім.

Жазық фигуралардың аудандарын табу

Аймақ мәселесі жалпақ фигурақарсы туындыларды табу мәселесімен (интеграция) тығыз байланысты. Атап айтқанда: функцияның графигімен шектелген қисық сызықты трапеция ауданыy=f(x) (f(x)> 0) түзуx=a; x=b; у= 0, функция үшін антитуынды мәндерінің айырмашылығына теңy=f(x) нүктелердеб Жәнеа :

S=F(b)–F(a)

Анықтама берейік анықталған интеграл.

ТУРАЛЫ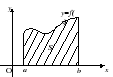
анықтамасы.Функция болсын y=f(x)интервалда анықталған және интегралданатын [ а,б] және рұқсат етіңіз F(x)- оның кейбір прототиптері. Содан кейін нөмір F(b)–F(a)-ның интегралы деп аталады Адейін бфункциялары f(x)және тағайындалады

.

Теңдік
Ньютон-Лейбниц формуласы деп аталады.

Бұл формула интегралмен жазық фигураның ауданын табу есебін байланыстырады.

Жалпы, егер фигура функция графиктерімен шектелсе y=f(x);y=g(x) (f(x)>g(x)) және түзу x=a;x=b, онда оның ауданы тең болады:

.

2-мысал.Функция графигінің қай нүктесінде y=x 2 + 1 осы функцияның графигі мен түзулері арқылы құрылған фигураны кесіп тастайтындай етіп тангенс салу керек. у= 0, x= 0, x=Ауданы ең үлкен 1 трапеция?

Шешім.Болсын М 0 (x 0 , ж 0 ) – функция графигінің нүктесі y=x 2 + 1, онда қажетті жанама сызылады.

Тангенс теңдеуін табайық y=y 0 +f (x 0 )(x–x 0 ) .

Бізде бар:

Сондықтан

.

Трапецияның ауданын табыңыз OABC.

.

Б– жанаманың түзумен қиылысу нүктесі x= 1 

Тапсырма іздеуге келді ең жоғары мәнфункциялары

С(x)=–x 2 +x+сегментте 1. Біз табамыз С (x)=– 2x+ 1. Шарттан критикалық нүктені табыңыз С (x)= 0  x=.

Функцияның ең үлкен мәніне жеткенін көреміз x=. Біз табамыз
.

Жауап:нүктесінде жанама жүргізілуі керек
.

Интегралды оның геометриялық мағынасына қарай табу мәселесі жиі кездесетінін ескеріңіз. Бұл мәселенің қалай шешілетінін мысалмен көрсетейік.

4-мысал.Интегралдың геометриялық мағынасын пайдаланып, есептеңіз

А )
; б)
.

Шешім.

A)
– ауданына теңқисық трапеция, сызықтармен шектеледі.

П түрлендірейік

– центрі бар шеңбердің жоғарғы жартысы Р(1;0) және радиусы R= 1.

Сондықтан
.

Жауап:
.

б) Дәл осылай дәлелдей отырып, .2 графиктерімен шектелген ауданды тұрғызайық – 2x+ 2, нүктелерде оған жанама А
, Б(4;2)

у=–9x– 59, парабола у= 3x 2 +балта+ 1, егер нүктедегі параболаға жанама болатыны белгілі болса x=– 2 осьпен Өгізбұрыш өлшемі arctg 6.

Табу А, егер қисық сызықты трапеция ауданы сызықтармен шектелетіні белгілі болса у= 3x 3 + 2x, x=a, y= 0 бірге тең.

Табу ең кіші мәнпараболамен шектелген фигураның ауданы y=x 2 + 2x– 3 және түзу y=kx+ 1.

6.Үй тапсырмасын ақпараттандыру кезеңі.

Міндеттері: Оқушылардың No18, 19,20,21 тақ үй тапсырмасын орындаудың мақсатын, мазмұнын және әдістерін түсінуін қамтамасыз ету

7. Сабақты қорытындылау.

Мақсаты: Сыныптың және жекелеген оқушылардың жұмысына сапалы баға беру.

Интегралдық есептеудің қосымшаларын қарастыруға көшейік. Бұл сабақта біз әдеттегі және ең көп таралған тапсырманы талдаймыз Анықталған интеграл көмегімен жазық фигураның ауданын есептеу. Ақырында бәрі мағынаны іздейді жоғары математика- оны тауып алсын. Сіз ешқашан білмейсіз. Нақты өмірде сізге қарапайым функцияларды пайдаланып саяжай учаскесін жуықтап, белгілі бір интеграл арқылы оның ауданын табу керек.

Материалды сәтті меңгеру үшін сізге қажет:

1) Түсіну анықталмаған интегралкем дегенде орташа деңгейде. Осылайша, манекендер алдымен сабақты оқуы керек Жоқ.

2) Ньютон-Лейбниц формуласын қолдана білу және анықталған интегралды есептей алу. Беттегі белгілі бір интегралдармен жылы достық қарым-қатынас орнатуға болады Анықталған интеграл. Шешімдердің мысалдары. «Анықталған интеграл көмегімен ауданды есептеу» тапсырмасы әрқашан сызбаны салуды қамтиды, сондықтан сіздің біліміңіз бен сурет салу дағдыларыңыз да өзекті мәселе болады. Кем дегенде түзу, парабола және гипербола құра білу керек.

Қисық трапециядан бастайық. Қисық трапеция – бұл қандай да бір функцияның графигімен шектелген жазық фигура ж = f(x), ось ӨҚжәне сызықтар x = а; x = б.

Қисық сызықты трапецияның ауданы белгілі бір интегралға сандық түрде тең

Кез келген белгілі бір интеграл (бар) өте жақсы геометриялық мағынаға ие. Сыныпта Анықталған интеграл. Шешімдердің мысалдарыанықталған интегралды сан деп айттық. Енді тағы бір пайдалы фактіні айтудың уақыты келді. Геометрия тұрғысынан анықталған интеграл AREA болып табылады. Яғни, анықталған интеграл (егер ол бар болса) белгілі бір фигураның ауданына геометриялық түрде сәйкес келеді. Анықталған интегралды қарастырайық

Интеграл

жазықтықта қисық сызықты анықтайды (қажет болса, оны салуға болады), ал анықталған интегралдың өзі сәйкес қисық сызықты трапецияның ауданына сандық түрде тең.

1-мысал

, , , .

Бұл әдеттегі тапсырма мәлімдемесі. Ең маңызды нүктешешімдер – сызу. Сонымен қатар, сызбаны салу керек ДҰРЫС.

Сызбаны салу кезінде мен келесі тәртіпті ұсынамын: басындабарлық түзу сызықтарды (егер олар бар болса) және тек қана салған дұрыс Содан кейін– парабола, гипербола, басқа функциялардың графиктері. Нүкте бойынша құрылыс техникасын анықтамалық материалдан табуға болады Графиктер және қасиеттер элементар функциялар . Онда сіз біздің сабағымыз үшін өте пайдалы материалды таба аласыз - параболаны қалай тез салу керек.

Бұл мәселеде шешім келесідей болуы мүмкін.

Сызбаны жасайық (теңдеу екенін ескеріңіз ж= 0 осьті анықтайды ӨҚ):

Біз қисық трапецияны көлеңкелемейміз, бұл жерде қай аймақ екені анық туралы айтып отырмыз. Шешім келесідей жалғасады:

Сегмент бойынша [-2; 1] функция графигі ж = x 2 + 2 орналасқан осьтің үстіндеӨҚ, Сондықтан:

Жауап: .

Анықталған интегралды есептеуде және Ньютон-Лейбниц формуласын қолдануда кім қиындықтарға тап болады?

,

лекцияға жүгініңіз Анықталған интеграл. Шешімдердің мысалдары. Тапсырма орындалғаннан кейін сызбаға қарап, жауаптың нақты екенін анықтау әрқашан пайдалы. Бұл жағдайда біз сызбадағы ұяшықтардың санын «көзбен» санаймыз - жақсы, шамамен 9 болады, бұл дұрыс сияқты. Егер біз жауап алсақ, айталық: 20 екені анық шаршы бірлік, содан кейін бір жерде қате жіберілгені анық - 20 ұяшық қаралған фигураға сәйкес келмейтіні анық, ең көп дегенде ондаған. Жауап теріс болса, тапсырма да қате шешілген.

2-мысал

Сызықтармен шектелген фигураның ауданын есептеңіз xy = 4, x = 2, x= 4 және ось ӨҚ.

Бұл үшін мысал тәуелсіз шешім. Толық шешімжәне сабақтың соңында жауап береді.

Қисық трапеция орналасса не істеу керек осьтің астындаӨҚ?

3-мысал

Сызықтармен шектелген фигураның ауданын есептеңіз ж = e-x, x= 1 және координаталық осьтер.

Шешуі: Сурет салайық:

Егер қисық трапеция болса толығымен осьтің астында орналасқан ӨҚ , онда оның ауданын мына формула арқылы табуға болады:

Бұл жағдайда:

.

Назар аударыңыз! Тапсырмалардың екі түрін шатастыруға болмайды:

1) Ешқандай геометриялық мағынасы жоқ белгілі бір интегралды шешу сұралса, ол теріс болуы мүмкін.

2) Егер сізге белгілі интеграл көмегімен фигураның ауданын табу сұралса, онда аудан әрқашан оң болады! Міне, сондықтан минус жаңа талқыланған формулада пайда болады.

Іс жүзінде фигура көбінесе жоғарғы және төменгі жарты жазықтықта орналасады, сондықтан қарапайым мектеп есептерінен біз мағыналы мысалдарға көшеміз.

4-мысал

Түзулермен шектелген жазықтық фигураның ауданын табыңыз ж = 2x – x 2 , ж = -x.

Шешуі: Алдымен сурет салу керек. Аудан есептерінің сызбасын құрастыру кезінде бізді сызықтардың қиылысу нүктелері қызықтырады. Параболаның қиылысу нүктелерін табайық ж = 2x – x 2 және түзу ж = -x. Мұны екі жолмен жасауға болады. Бірінші әдіс аналитикалық. Теңдеуді шешеміз:

Бұл интеграцияның төменгі шегі дегенді білдіреді а = 0, жоғарғы шегіинтеграция б= 3. Сызықтарды нүкте бойынша салу жиі тиімдірек және жылдамырақ, ал интеграцияның шекаралары «өздігінен» анық болады. Осыған қарамастан, шектерді табудың аналитикалық әдісін әлі де кейде қолдануға тура келеді, егер, мысалы, график жеткілікті үлкен болса немесе егжей-тегжейлі конструкция интеграцияның шектерін ашпаса (олар бөлшек немесе иррационалды болуы мүмкін). Тапсырмамызға оралайық: алдымен түзу, содан кейін ғана парабола салу ұтымдырақ. Сызбаны жасайық:

Қайталап айтайық, нүктелік тұрғызу кезінде интеграцияның шектері көбінесе «автоматты түрде» анықталады.

Ал енді жұмыс формуласы:

Егер сегментте [ а; б] кейбір үздіксіз функция f(x) артық немесе теңкейбір үздіксіз функция g(x), онда сәйкес фигураның ауданын мына формула арқылы табуға болады:

Мұнда фигураның қай жерде орналасқаны туралы ойлаудың қажеті жоқ - осьтің үстінде немесе осьтің астында, бірақ қай графтың ЖОҒАРЫ екені маңызды(басқа графикке қатысты), және қайсысы ТӨМЕН.

Қарастырылып отырған мысалда парабола кесіндіде түзу сызықтың үстінде орналасқаны анық, демек 2-ден x – x 2 алу керек – x.

Аяқталған шешім келесідей болуы мүмкін:

Қажетті фигура параболамен шектелген ж = 2x – x 2 жоғарғы және түзу ж = -xтөменде.

2-сегментте x – x 2 ≥ -x. Сәйкес формула бойынша:

Жауап: .

Шындығында, төменгі жарты жазықтықтағы қисық сызықты трапеция ауданына арналған мектеп формуласы (№ 3 мысалды қараңыз) ерекше жағдайформулалар

.

Өйткені ось ӨҚтеңдеуімен берілген ж= 0 және функцияның графигі g(x) осьтің астында орналасқан ӨҚ, Бұл

.

Ал енді сіздің жеке шешіміңізге бірнеше мысал

5-мысал

6-мысал

Түзулермен шектелген фигураның ауданын табыңыз

Анықталған интегралдың көмегімен ауданды есептеуге байланысты есептерді шешу кезінде кейде күлкілі оқиға орын алады. Сызба дұрыс салынды, есептеулер дұрыс болды, бірақ абайсыздықтан... Қате фигураның ауданы табылды.

7-мысал

Алдымен сурет салайық:

Ауданын табуымыз керек фигура көк түсті(шартты мұқият қараңыз - фигура қалай шектелген!). Бірақ іс жүзінде, назар аудармау салдарынан адамдар көбінесе жасыл түспен боялған фигураның ауданын табу керек деп шешеді!

Бұл мысал да пайдалы, себебі ол екі анықталған интегралды пайдаланып фигураның ауданын есептейді. Шынымен:

1) кесінді бойынша [-1; 1] осінен жоғары ӨҚграфик түзу орналасқан ж = x+1;

2) ось үстіндегі сегментте ӨҚгиперболаның графигі орналасқан ж = (2/x).

Аймақтарды қосуға болатыны (және қажет) екені анық, сондықтан:

Жауап:

8-мысал

Сызықтармен шектелген фигураның ауданын есептеңіз

Теңдеулерді «мектеп» түрінде көрсетейік

және нүкте бойынша сызба жасаңыз:

Сызбадан біздің жоғарғы шегіміз «жақсы» екені анық: б = 1.

Бірақ төменгі шегі қандай?! Бұл бүтін сан емес екені анық, бірақ бұл не?

Мүмкін, а=(-1/3)? Бірақ сызбаның мінсіз дәлдікпен жасалғанына кепілдік қайда, бұл жақсы болуы мүмкін а=(-1/4). Егер графикті қате құрастырсақ ше?

Мұндай жағдайларда қосымша уақыт жұмсауға және интеграцияның шектерін аналитикалық түрде нақтылауға тура келеді.

Графиктердің қиылысу нүктелерін табайық

Ол үшін мына теңдеуді шешеміз:

.

Демек, а=(-1/3).

Бұдан әрі шешім тривиальды. Ең бастысы - ауыстырулар мен белгілерде шатастырмау. Мұндағы есептеулер қарапайым емес. Сегментте

, ,

сәйкес формула бойынша:

Жауап:

Сабақты қорытындылау үшін тағы екі қиын тапсырманы қарастырайық.

9-мысал

Сызықтармен шектелген фигураның ауданын есептеңіз

Шешуі: Осы фигураны сызбада бейнелеп көрейік.

Нүкте-нүкте сызбасын салу үшін білу керек сыртқы түрісинусоидтар. Жалпы алғанда, барлық элементар функциялардың графиктерін, сондай-ақ кейбір синус мәндерін білу пайдалы. Оларды мәндер кестесінен табуға болады тригонометриялық функциялар . Кейбір жағдайларда (мысалы, бұл жағдайда) схемалық сызбаны салуға болады, онда интеграцияның графиктері мен шектері түбегейлі дұрыс көрсетілуі керек.

Бұл жерде интеграциялық шектеулер бойынша проблемалар жоқ, олар тікелей шарттан туындайды:

– «x» нөлден «piге» өзгереді. Қосымша шешім қабылдасақ:

Сегментте функцияның графигі ж= күнә 3 xосінен жоғары орналасқан ӨҚ, Сондықтан:

(1) Сабақта синустар мен косинустардың тақ дәрежелерде қалай біріктірілгенін көруге болады Тригонометриялық функциялардың интегралдары. Біз бір синусты қысамыз.

(2) Біз формада негізгі тригонометриялық сәйкестікті қолданамыз

(3) Айнымалыны өзгертейік т=cos x, онда: осьтің үстінде орналасқан, сондықтан:

.

.

Ескерту:мұнда негізгі тригонометриялық сәйкестіктің нәтижесі жанама текшенің интегралы қалай алынғанын ескеріңіз;

.

Кіріспе

f(x) функциясының f" (x) туындысын немесе df=f" (x) dx дифференциалын табу дифференциалдық есептеудің негізгі мәселесі болып табылады. Интегралдық есепте кері есеп шешіледі: f(x) функциясы берілгенде, F" (x)=f(x) немесе F(x)=F" болатындай F(x) функциясын табу қажет. x) dx=f(x )dx. Сонымен, интегралдық есептеудің негізгі міндеті - бұл функцияның белгілі туындысынан (дифференциалынан) F(x) функциясын қалпына келтіру. Интегралдық есептеулер геометрияда, механикада, физикада және технологияда көптеген қолданбаларға ие. Ол береді жалпы әдісаудандарды, көлемдерді, ауырлық центрлерін табу және т.б.

Жақсы математикалық талдауәр түрлі материалды қамтиды, дегенмен оның орталық бөлімдерінің бірі белгілі интеграл болып табылады. Функциялардың көптеген түрлерін интегралдау кейде математикалық талдаудағы ең қиын есептердің бірі болып табылады.

Анықталған интегралды есептеу тек теориялық қызығушылық тудырмайды. Кейде адамның практикалық іс-әрекетіне байланысты мәселелер оның есебіне түседі.

Сондай-ақ физикада анықталған интеграл ұғымы кеңінен қолданылады.

Қисық трапецияның ауданын табу

Қисық трапеция деп тікбұрышты координаталар жүйесінде орналасқан және х осімен және түзу сызықтармен шектелген фигураны айтады. x = aЖәне x = bжәне қисық және сегментте теріс емес. Қисық трапецияның шамамен ауданын келесідей табуға болады:

1. х осінің сегментін бөліңіз nтең сегменттер;

2. абсцисса осіне перпендикуляр кесінділерді бөлу нүктелері арқылы қисық сызықпен қиылысқанша жүргіземіз;

3. алынған бағандарды негізі мен биіктігі бар тіктөртбұрыштармен ауыстырыңыз, мәніне теңфункциялары fәрбір сегменттің сол жағында;

4. осы төртбұрыштардың аудандарының қосындысын табыңдар.

Бірақ қисық сызықты ауданды басқаша табуға болады: Ньютон-Лейбниц формуласы арқылы. Олардың атаулары бар формуланы дәлелдеу үшін қисық сызықты трапеция ауданы тең екенін дәлелдейміз, мұндағы графигі қисық сызықты трапецияны шектейтін функцияның кез келген қарсы туындысы.

Қисық трапецияның ауданын есептеу былай жазылады:

1. функцияның кез келген қарсы туындысы табылды.

2. жазылады. - Бұл Ньютон-Лейбниц формуласы.

Қисық сектордың ауданын табу

Қисықты қарайық? = ? (?) V полярлық жүйекоординаттары, қайда? (?) - [? бойынша үздіксіз және теріс емес; ?] функциясы. Қисық сызықпен шектелген фигура? (?) және сәулелер? = ?, ? = ?, қисық сызықты сектор деп аталады. Қисық сызықты сектордың ауданы тең

Қисық доғаның ұзындығын табу

Тік бұрышты координаталар

АВ жазық қисығы тікбұрышты координаталарда берілсін, оның теңдеуі у = f(x), мұндағы а? x? б. (2-сурет)

АВ доғасының ұзындығы деп сынық сызықтың буындарының саны шексіз өскенде, ал оның ең үлкен буынының ұзындығы нөлге ұмтылғанда, осы доғаға сызылған сынық сызықтың ұзындығы ұмтылатын шегі түсініледі.

I схеманы қолданайық (қосынды әдісі).

X = a, X, …, X = b (X ? X? … ? X) нүктелерін пайдаланып кесіндіні n бөлікке бөлеміз. Бұл нүктелер АВ қисығының M = A, M, …, M = B нүктелеріне сәйкес болсын. Ұзындықтары сәйкесінше ?L, ?L, …, ?L деп белгіленетін MM, MM, …, MM хордаларын салайық.

Ұзындығы L = ?L+ ?L+ ... + ?L = ?L тең болатын MMM ... MM сынық сызықты аламыз.

?L хордасының (немесе сынық сызықтың) ұзындығын ?X және ?Y катеттері бар үшбұрыштан Пифагор теоремасы арқылы табуға болады:

L = , мұндағы?X = X - X, ?Y = f(X) - f(X).

Функцияның ақырлы өсімі туралы Лагранж теоремасы бойынша

Y = (C) ?X, мұндағы C (X, X).

және бүкіл сынық сызықтың ұзындығы MMM...MM тең

АВ қисығының ұзындығы анықтамасы бойынша тең

Назар аударыңыз, қашан ?L 0 сонымен қатар ?X 0 (?L = және сондықтан | ?X |< ?L). Функция непрерывна на отрезке , так как, по условию, непрерывна функция f (X). Следовательно, существует предел интегральной суммы L=?L= , кода max ?X 0:

Осылайша L = dx.

Мысал: Радиусы R шеңбердің шеңберін табыңыз (3-сурет)

Біз оны табамыз ба? оның (0; R) нүктесінен (R; 0) нүктесіне дейінгі ұзындығының бір бөлігі. Өйткені

Мысал 1 . Түзулермен шектелген фигураның ауданын есептеңіз: x + 2y – 4 = 0, y = 0, x = -3, және x = 2

Фигураны тұрғызайық (суретті қараңыз) Екі A(4;0) және B(0;2) нүктелерін пайдаланып x + 2y – 4 = 0 түзуін саламыз. у-ді х арқылы өрнектесек, у = -0,5x + 2 аламыз. (1) формуланы қолданып, мұндағы f(x) = -0,5x + 2, a = -3, b = 2, табамыз.

S = = [-0,25=11,25 кв. бірлік

2-мысал. Түзулермен шектелген фигураның ауданын есептеңіз: x – 2y + 4 = 0, x + y – 5 = 0 және y = 0.

Шешім. Фигураны құрастырайық.

x – 2y + 4 = 0 түзуін тұрғызайық: y = 0, x = - 4, A(-4; 0); x = 0, y = 2, B(0; 2).

x + y – 5 = 0 түзуін салайық: y = 0, x = 5, C(5; 0), x = 0, y = 5, D(0; 5).

Теңдеулер жүйесін шешу арқылы түзулердің қиылысу нүктесін табайық:

x = 2, y = 3; M(2; 3).

Қажетті ауданды есептеу үшін AMC үшбұрышын екі AMN және NMC үшбұрыштарына бөлеміз, өйткені х А-дан N-ге өзгергенде аудан түзумен, ал х N-ден С-ға өзгергенде - түзу сызықпен шектеледі.

AMN үшбұрышы үшін бізде: ; y = 0,5x + 2, яғни f(x) = 0,5x + 2, a = - 4, b = 2.

NMC үшбұрышы үшін бізде: y = - x + 5, яғни f(x) = - x + 5, a = 2, b = 5.

Әрбір үшбұрыштың ауданын есептеп, нәтижелерді қосу арқылы біз табамыз:

шаршы бірлік

шаршы бірлік

9 + 4, 5 = 13,5 ш. бірлік Тексеріңіз: = 0,5АС = 0,5 кв. бірлік

3-мысал. Түзулермен шектелген фигураның ауданын есептеңіз: y = x 2 , у = 0, x = 2, x = 3.

Бұл жағдайда у = x параболасымен шектелген қисық трапецияның ауданын есептеу керек. 2 , түзу сызықтар x = 2 және x = 3 және Ox осі (суретті қараңыз) (1) формуланы пайдаланып, қисық сызықты трапецияның ауданын табамыз

= = 6 шаршы бірлік

4-мысал. Түзулермен шектелген фигураның ауданын есептеңіз: y = - x 2 + 4 және у = 0

Фигураны құрастырайық. Қажетті аудан у = - х параболасының арасына алынған 2 + 4 және Ox осі.

Параболаның Окс осімен қиылысу нүктелерін табайық. y = 0 деп есептесек, біз x = табамыз, бұл фигура Oy осіне қатысты симметриялы болғандықтан, біз Oy осінің оң жағында орналасқан фигураның ауданын есептеп, алынған нәтижені екі есе көбейтеміз: = +4x]sq. бірлік 2 = 2 шаршы бірлік

5-мысал. Түзулермен шектелген фигураның ауданын есептеңіз: у 2 = x, yx = 1, x = 4

Мұнда параболаның жоғарғы тармағымен шектелген қисық сызықты трапецияның ауданын есептеу керек. 2 = x, Ox осі және түзу сызықтар x = 1 және x = 4 (суретті қараңыз)

(1) формуласына сәйкес, мұндағы f(x) = a = 1 және b = 4, бізде = (= шаршы бірліктері бар.

6-мысал . Түзулермен шектелген фигураның ауданын есептеңіз: y = sinx, y = 0, x = 0, x= .

Қажетті аймақ синусоидтың жарты толқыны мен Ox осімен шектеледі (суретті қараңыз).

Бізде - cosx = - cos = 1 + 1 = 2 шаршы. бірлік

7-мысал. Түзулермен шектелген фигураның ауданын есептеңіз: y = - 6x, y = 0 және x = 4.

Сурет Ox осінің астында орналасқан (суретті қараңыз).

Сондықтан оның ауданын (3) формула арқылы табамыз.

= =

8-мысал. Түзулермен шектелген фигураның ауданын есептеңіз: y = және x = 2. Нүктелерден у = қисығын салыңыз (суретті қараңыз). Осылайша, (4) формуласы арқылы фигураның ауданын табамыз.

9-мысал .

X 2 + ж 2 = r 2 .

Мұнда x шеңберімен қоршалған ауданды есептеу керек 2 + ж 2 = r 2 , яғни центрі координат басында болатын радиусы r шеңберінің ауданы. 0-ден интегралдау шегін алып, осы ауданның төртінші бөлігін табайық

бұрын; бізде бар: 1 = = [

Демек, 1 =

10-мысал. Түзулермен шектелген фигураның ауданын есептеңдер: y= x 2 және y = 2x

Бұл көрсеткіш у = х параболасымен шектелген 2 және түзу у = 2х (суретті қараңыз) Берілген түзулердің қиылысу нүктелерін анықтау үшін теңдеулер жүйесін шешеміз: x 2 – 2x = 0 x = 0 және x = 2

Ауданды табу үшін (5) формуланы қолданып аламыз

= }