Vector. Basic properties

Definition An ordered collection (x 1, x 2, ..., x n) n real numbers is called n-dimensional vector, and the numbers x i (i = 1, ..., n) are components or coordinates,

Example. If, for example, a certain automobile plant has to produce 50 cars, 100 trucks, 10 buses, 50 sets of spare parts for cars and 150 sets for trucks and buses per shift, then the production program of this plant can be written in the form of a vector (50, 100 , 10, 50, 150) having five components.

Notation. Vectors are denoted in bold lowercase letters or letters with a bar or arrow at the top, for example, a or . The two vectors are called equal if they have the same number of components and their corresponding components are equal.

Vector components cannot be swapped, for example, (3, 2, 5, 0, 1) and (2, 3, 5, 0, 1) are different vectors.
Operations on vectors. By productx= (x 1, x 2, ..., x n) by a real number λ is called a vector λ x= (λ x 1, λ x 2, ..., λ x n).

The sumx= (x 1, x 2, ..., x n) and y= (y 1, y 2, ..., y n) is called the vector x + y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

Space of vectors. N-dimensional vector space R n is defined as the set of all n-dimensional vectors for which the operations of multiplication by real numbers and addition are defined.

Economic illustration. Economic illustration of n-dimensional vector space: space of goods (goods). Under commodity we will understand some good or service that went on sale at a certain time in a certain place. Suppose there is a finite number of items on hand, n; the quantities of each of them purchased by the consumer are characterized by a set of goods

x= (x 1, x 2, ..., x n),

where x i denotes the amount of the i-th good purchased by the consumer. We will assume that all goods have the property of arbitrary divisibility, so that any non-negative amount of each of them can be bought. Then all possible sets of goods are vectors of the space of goods C = ( x= (x 1, x 2, ..., x n) x i ≥ 0, i = 1, ..., n).

Linear independence. System e 1 , e 2 , ... , e m n-dimensional vectors is called linearly dependent if there are numbers λ 1, λ 2, ..., λ m such that at least one of them is nonzero such that λ 1 e 1 + λ m e m = 0; otherwise, this system of vectors is called linearly independent, that is, the indicated equality is possible only in the case when all λ 1 = λ 2 = ... = λ m = 0. The geometric meaning of the linear dependence of vectors in R 3, interpreted as directed segments, explain the following theorems.

Theorem 1. A system consisting of one vector is linearly dependent if and only if this vector is zero.

Theorem 2. In order for two vectors to be linearly dependent, it is necessary and sufficient that they be collinear (parallel).

Theorem 3 ... In order for three vectors to be linearly dependent, it is necessary and sufficient that they be coplanar (lie in the same plane).

Left and right triplets of vectors. Three non-coplanar vectors a, b, c called right if the observer from their common origin traverses the ends of the vectors a, b, c in the order shown, it appears to be clockwise. Otherwise a, b, c -left triple... All right (or left) triplets of vectors are called equally oriented.

Basis and coordinates. Troika e 1, e 2 , e 3 non-coplanar vectors in R 3 is called basis, and the vectors themselves e 1, e 2 , e 3 - basic... Any vector a can be uniquely expanded in terms of basis vectors, that is, represented in the form

a= x 1 e 1 + x 2 e 2 + x 3 e 3, (1.1)

the numbers x 1, x 2, x 3 in the expansion (1.1) are called coordinatesa in the basis e 1, e 2 , e 3 and are denoted a(x 1, x 2, x 3).

Orthonormal basis. If vectors e 1, e 2 , e 3 are pairwise perpendicular and the length of each of them is equal to one, then the basis is called orthonormal, and coordinates x 1, x 2, x 3 - rectangular. The basis vectors of the orthonormal basis will be denoted by i, j, k.

We will assume that in space R 3 the right system of Cartesian rectangular coordinates is selected (0, i, j, k}.

Vector product.Vector producta per vector b is called a vector c, which is determined by the following three conditions:

1. Vector length c is numerically equal to the area of ​​a parallelogram built on vectors a and b, i.e.
c= | a || b | sin ( a^b).

2. Vector c perpendicular to each of the vectors a and b.

3. Vectors a, b and c taken in the indicated order form a right-hand triplet.

For vector product c the notation is introduced c =[ab] or
c = a × b.

If vectors a and b collinear, then sin ( a ^ b) = 0 and [ ab] = 0, in particular, [ aa] = 0. Vector products of unit vectors: [ ij]=k, [jk] = i, [ki]=j.

If vectors a and b given in the basis i, j, k coordinates a(a 1, a 2, a 3), b(b 1, b 2, b 3), then

Mixed work. If the cross product of two vectors a and b scalar multiplied by the third vector c, then such a product of three vectors is called mixed work and is denoted by the symbol a b c.

If vectors a, b and c in the basis i, j, k given by their coordinates
a(a 1, a 2, a 3), b(b 1, b 2, b 3), c(c 1, c 2, c 3), then

.

The mixed product has a simple geometric interpretation - it is a scalar equal in absolute value to the volume of a parallelepiped built on these three vectors.

If the vectors form a right-hand triplet, then their mixed product is a positive number equal to the indicated volume; if the three a, b, c - left, then a b c<0 и V = - a b c, therefore V = | a b c |.

The coordinates of vectors encountered in the problems of the first chapter are assumed to be given with respect to the right orthonormal basis. Unit vector codirectional to vector a, denoted by the symbol a O. Symbol r=OM denoted by the radius vector of the point M, symbols a, AB or | a |, |AB | the modules of vectors a and AB.

Example 1.2. Find the angle between vectors a= 2m+4n and b= m-n, where m and n - unit vectors and angle between m and n is equal to 120 p.

Solution... We have: cos φ = ab/ ab, ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4 + 2cos120 o = - 2 + 2 (-0.5) = -3; a = ; a 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4 + 16 (-0.5) + 16 = 12, so a =. b = ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 = 1-2 (-0.5) +1 = 3, so b =. Finally, we have: cos φ == -1/2, φ = 120 o.

Example 1.3. Knowing vectors AB(-3, -2.6) and BC(-2,4,4), calculate the length of the height AD of triangle ABC.

Solution... Denoting the area of ​​triangle ABC through S, we get:
S = 1/2 BC AD. Then AD = 2S / BC, BC = = = 6,
S = 1/2 | AB ×AC |. AC = AB + BC, so the vector AC has coordinates
.

DEFINITION

Vector(from lat. " vector"-" bearing ") - a directed segment of a straight line in space or on a plane.

Graphically, a vector is depicted as a directed line segment of a certain length. A vector, the beginning of which is at a point, and the end at a point, is denoted as (Fig. 1). Also, a vector can be denoted with one small letter, for example,.

If a coordinate system is specified in space, then the vector can be uniquely specified by a set of its coordinates. That is, a vector is understood as an object that has a magnitude (length), direction and point of application (the beginning of the vector).

The beginnings of vector calculus appeared in works in 1831 in the works of the German mathematician, mechanic, physicist, astronomer and surveyor Johann Karl Friedrich Gauss (1777-1855). Works on operations with vectors were published by the Irish mathematician, mechanic and theoretical physicist, Sir William Rowan Hamilton (1805-1865) in the framework of his quaternion calculus. The scientist proposed the term "vector" and described some operations on vectors. Vector calculus was further developed thanks to the work on electromagnetism by the British physicist, mathematician and mechanic James Clerk Maxwell (1831-1879). In the 1880s, the book "Elements of Vector Analysis" was published by the American physicist, physicochemist, mathematician and mechanic Josiah Willard Gibbs (1839-1903). Modern vector analysis was described in 1903 by the English self-taught scientist, engineer, mathematician and physicist Oliver Heaviside (1850-1925).

DEFINITION

Length or vector module is the length of the directed segment that defines the vector. It is indicated as.

Basic types of vectors

Zero vector is a vector whose start point and end point coincide. The length of the zero vector is zero.

Vectors parallel to one straight line or lying on one straight line are called collinear(fig. 2).

co-directed if their directions are the same.

In Figure 2, these are vectors and. The co-directionality of vectors is denoted as follows:.

Two collinear vectors are called oppositely directed if their directions are opposite.

In Figure 3, these are vectors and. Designation:.

VECTORS... ACTIONSABOVEVECTORS. SCALAR,

VECTOR, MIXED PRODUCT OF VECTORS.

1. VECTORS, ACTIONS ON VECTORS.

Basic definitions.

Definition 1. A quantity fully characterized by its numerical value in the chosen system of units is called scalar or scalar .

(Body weight, volume, time, etc.)

Definition 2. A quantity characterized by a numerical value and direction is called vector or vector .

(Displacement, strength, speed, etc.)

Designations:, or,.

A geometric vector is a directional line.

For a vector - a point A- start, point V- the end of the vector.

Definition 3.Module vector is the length of the segment AB.

Definition 4. A vector whose modulus is equal to zero is called zero , indicated by.

Definition 5. Vectors located on parallel lines or on one line are called collinear ... If two collinear vectors have the same direction, then they are called co-directed .

Definition 6. Two vectors are considered equal , if they co-directed and are equal in absolute value.

Actions on vectors.

1) Addition of vectors.

Def. 6.The sum two vectors and is the diagonal of the parallelogram built on these vectors, starting from the common point of their application (parallelogram rule).

Fig. 1.

Def. 7. The sum of three vectors,, is called the diagonal of the parallelepiped built on these vectors (box rule).

Def. eight. If A, V, WITH - arbitrary points, then + = (triangle rule).

fig. 2

Addition properties.

1 O . + = + (transpositional law).

2 O . + (+) = (+) + = (+) + (combination law).

3 O . + (– ) + .

2) Subtraction of vectors.

Def. nine. Under difference vectors and understand vector = - such that + = .

In a parallelogram, this is another diagonal SD (see Figure 1).

3) Multiplying a vector by a number.

Def. ten. By product vectors per scalar k is called a vector

= k = k ,

long ka , and the direction of which:

1.coincides with the direction of the vector if k > 0;

2.Opposite to the direction of the vector, if k < 0;

3. arbitrarily if k = 0.

Properties of multiplying a vector by a number.

1 O . (k + l ) = k + l .

k ( + ) = k + k .

2 o . k (l ) = (kl ) .

3 o . 1  = , (–1)  = – , 0  = .

Vector properties.

Def. eleven. Two vectors and are called collinear if they are located on parallel lines or at one straight line.

A null vector is collinear to any vector.

Theorem 1. Two nonzero vectors and collinear,  when they are proportional i.e.

= k , k Is a scalar.

Def. 12. Three vectors,, are called coplanar if they are parallel to some plane or lie in it.

Theorem 2. Three nonzero vectors,, coplanar,  when one of them is a linear combination of the other two, i.e.

= k + l , k , l - scalars.

The projection of the vector to the axis.

Theorem 3. Projection of a vector onto an axis (directed straight line) l is equal to the product of the length of the vector and the cosine of the angle between the direction of the vector and the direction of the axis, i.e. = a  c os  ,  = ( , l).

2. VECTOR COORDINATES

Def. 13. Vector projections on coordinate axes Oh, OU, Оz are called vector coordinates. Designation:  a x , a y , a z .

Vector length:

Example: Calculate the length of the vector.

Solution:

Distance between points and calculated by the formula: .

Example: Find the distance between the points M (2,3, -1) and K (4,5,2).

Actions on vectors in coordinate form.

Given vectors =  a x , a y , a z and =  b x , b y , b z .

1. (  )= a x  b x , a y  b y , a z  b z .

2.  =   a x ,  a y ,  a z, where  Is a scalar.

Dot product of vectors.

Definition: Under the dot product of two vectors and

is understood as a number equal to the product of the lengths of these vectors by the cosine of the angle between them, i.e. = , is the angle between vectors and.

Dot product properties:

1.  =

2. ( + ) =

3.

4.

5. , where are scalars.

6.two vectors are perpendicular (orthogonal) if .

7.if and only if .

The dot product in coordinate form is: , where and .

Example: Find the dot product of vectors and

Solution:

Vector holding vectors.

Definition: The vector product of two vectors is understood as a vector for which:

The modulus is equal to the area of ​​the parallelogram built on these vectors, i.e. , where the angle between vectors and

This vector is perpendicular to the vectors being multiplied, i.e.

If the vectors are not collinear, then they form the right triplet of vectors.

Vector product properties:

(1) When the order of the factors is changed, the vector product changes its sign to the opposite, preserving the modulus, i.e.

2 .The vector square is equal to the zero vector, i.e.

3 The scalar factor can be moved outside the sign of the vector product, i.e.

4 . For any three vectors, the equality

5 A necessary and sufficient condition for collinearity of two vectors and:

Vector product in coordinate form.

If the coordinates of the vectors and , then their cross product is found by the formula:

.

Then from the definition of a vector product it follows that the area of ​​a parallelogram built on vectors and is calculated by the formula:

Example: Calculate the area of ​​a triangle with vertices (1; -1; 2), (5; -6; 2), (1; 3; -1).

Solution: .

Then the area of ​​the triangle ABC will be calculated as follows:

,

Mixed product of vectors.

Definition: A mixed (vector-scalar) product of vectors is a number determined by the formula: .

Mixed work properties:

1. The mixed product does not change under cyclic permutation of its factors, i.e. .

2. Upon permutation of two adjacent factors, the mixed product changes its sign to the opposite, i.e. ...

3 A necessary and sufficient condition for the coplanarity of three vectors : =0.

4 The mixed product of three vectors is equal to the volume of the parallelepiped built on these vectors, taken with a plus sign if these vectors form a right triple, and with a minus sign if they form a left triple, i.e. .

If known coordinates vectors , then the mixed work is found by the formula:

Example: Calculate the mixed product of vectors.

Solution:

3. The basis of the system of vectors.

Definition. A system of vectors is understood as several vectors belonging to the same space R.

Comment. If the system consists of a finite number of vectors, then they are denoted by the same letter with different indices.

Example.

Definition. Any vector of the form = called a linear combination of vectors. The numbers are the coefficients of the linear combination.

Example. .

Definition... If the vector is a linear combination of vectors , then the vector is said to be linearly expressed in terms of vectors .

Definition. The vector system is called linearly independent if none of the vectors of the system can be like a linear combination of the rest of the vectors. Otherwise, the system is called linearly dependent.

Example... Vector system linearly dependent, since the vector .

Determination of the basis. A system of vectors forms a basis if:

1) it is linearly independent,

2) any vector of space is linearly expressed through it.

Example 1. Space basis:.

2. In the system of vectors vectors are the basis: is linearly expressed in terms of vectors.

Comment. To find the basis of a given vector system, you need to:

1) write the coordinates of the vectors into the matrix,

2) using elementary transformations to bring the matrix to a triangular form,

3) nonzero rows of the matrix will be the basis of the system,

4) the number of vectors in the basis is equal to the rank of the matrix.

There will be tasks for independent decision to which you can see the answers.

Vector concept

Before you learn all about vectors and operations on them, tune in to solving a simple problem. There is a vector of your entrepreneurship and a vector of your innovative abilities. The vector of entrepreneurship leads you to Goal 1, and the vector of innovative abilities leads to Goal 2. The rules of the game are such that you cannot move in the directions of these two vectors at once and achieve two goals at once. Vectors interact, or, in mathematical terms, some operation is performed on vectors. The result of this operation is the "Result" vector, which leads you to Goal 3.

Now tell me: the result of what operation on the vectors "Enterprise" and "Innovative abilities" is the vector "Result"? If you can't tell right away, don't be discouraged. As you progress through this lesson, you will be able to answer this question.

As we have already seen above, the vector necessarily goes from some point A in a straight line to some point B... Therefore, each vector has not only a numerical value - length, but also physical and geometric - directionality. This leads to the first and simplest definition of a vector. So, a vector is a directed segment going from a point A to the point B... It is designated as follows:.

And to start different vector operations , we need to get acquainted with one more vector definition.

A vector is a kind of representation of a point to which you want to get from some starting point. For example, a three-dimensional vector is usually written as (x, y, z) . Quite simply, these numbers represent how far it takes to travel in three different directions to get to a point.

Let a vector be given. Wherein x = 3 (right hand points to the right) y = 1 (left hand points forward) z = 5 (under the point there is a staircase leading up). According to this data, you will find a point by walking 3 meters in the direction indicated by the right hand, then 1 meter in the direction indicated by the left hand, and then a staircase awaits you and, climbing 5 meters, you will finally find yourself at the final point.

All other terms are refinements of the above explanation, necessary for various operations on vectors, that is, solving practical problems. Let's go through these stricter definitions, dwelling on typical vector problems.

Physical examples vector quantities can be the displacement of a material point moving in space, the speed and acceleration of this point, as well as the force acting on it.

Geometric vector presented in two-dimensional and three-dimensional space in the form directional segment... This is a segment, which distinguishes between the beginning and the end.

If A is the beginning of the vector, and B- its end, then the vector is denoted by a symbol or one lowercase letter. In the figure, the end of the vector is indicated by an arrow (Fig. 1)

Length(or module) of a geometric vector is the length of the segment generating it

The two vectors are called equal , if they can be aligned (if the directions coincide) by means of parallel transfer, i.e. if they are parallel, point in the same direction, and have equal lengths.

In physics, it is often considered anchored vectors given by the point of application, length and direction. If the point of application of the vector does not matter, then it can be transferred, maintaining the length and direction to any point in space. In this case, the vector is called free... We will agree to consider only free vectors.

Linear operations on geometric vectors

Multiplying a vector by a number

Product of vector by the number is called a vector obtained from a vector by stretching (at) or compression (at) by times, and the direction of the vector is preserved, if, and changes to the opposite, if. (Fig. 2)

It follows from the definition that the vectors and = are always located on one or on parallel lines. Such vectors are called collinear... (You can also say that these vectors are parallel, but in vector algebra it is customary to say "collinear".) The converse is also true: if vectors and are collinear, then they are related by the relation

Therefore, equality (1) expresses the collinearity condition for two vectors.

Addition and subtraction of vectors

When adding vectors, you need to know that sum vectors and is called a vector, the beginning of which coincides with the beginning of the vector, and the end - with the end of the vector, provided that the beginning of the vector is attached to the end of the vector. (Fig. 3)

This definition can be distributed over any finite number of vectors. Let space be given n free vectors. When adding several vectors, the closing vector is taken as their sum, the beginning of which coincides with the beginning of the first vector, and the end - with the end of the last vector. That is, if you attach the beginning of the vector to the end of the vector, and the beginning of the vector to the end of the vector, etc. and, finally, to the end of the vector - the beginning of the vector, then the sum of these vectors is the closing vector whose beginning coincides with the beginning of the first vector, and the end - with the end of the last vector. (Fig. 4)

The terms are called the components of the vector, and the formulated rule is polygon rule... This polygon may not be flat.

When you multiply a vector by -1, you get the opposite vector. The vectors and have the same length and opposite directions. Their sum gives zero vector whose length is zero. The direction of the zero vector is undefined.

In vector algebra, there is no need to consider separately the operation of subtraction: subtracting a vector from a vector means adding the opposite vector to the vector, i.e.

Example 1. Simplify expression:

.

,

that is, vectors can be added and multiplied by numbers in the same way as polynomials (in particular, also tasks on simplifying expressions). Usually, the need to simplify linearly similar expressions with vectors arises before calculating the products of vectors.

Example 2. The vectors and serve as the diagonals of the parallelogram ABCD (Fig. 4a). Express in terms of both vectors, and, which are the sides of this parallelogram.

Solution. The intersection point of the parallelogram diagonals divides each diagonal in half. We find the lengths of the vectors required in the problem statement either as half the sums of the vectors forming a triangle with the desired ones, or as half the differences (depending on the direction of the vector serving as the diagonal), or, as in the latter case, half the sum taken with a minus sign. The result is the vectors required in the problem statement:

There is every reason to believe that you have now correctly answered the question about the Entrepreneurship and Innovative Ability vectors at the beginning of this lesson. Correct answer: addition operation is performed on these vectors.

Solve vector problems yourself and then see solutions

How to find the length of the sum of vectors?

This task takes a special place in vector operations, as it involves the use of trigonometric properties. Let's say you come across a task like the following:

Given the lengths of the vectors and the length of the sum of these vectors. Find the length of the difference between these vectors.

Solutions for this and others similar tasks and an explanation of how to solve them - in the lesson " Vector addition: vector sum length and cosine theorem ".

And you can check the solution of such problems on Online calculator "Unknown side of a triangle (vector addition and cosine theorem)" .

Where are the products of vectors?

The vector-by-vector products are not linear operations and are considered separately. And we have Dot Product of Vectors and Vector and Mixed Product of Vectors tutorials.

Projection of a vector onto an axis

The projection of the vector onto the axis is equal to the product of the length of the projected vector by the cosine of the angle between the vector and the axis:

As you know, the projection of the point A on a straight line (plane) is the base of the perpendicular dropped from this point on a straight line (plane).

Let be an arbitrary vector (Fig. 5), and and be the projections of its beginning (points A) and end (points B) per axis l... (To construct a projection of a point A) on a straight line through the point A plane perpendicular to the straight line. The intersection of the line and plane will define the required projection.

Vector component on the l-axis is called a vector lying on this axis, the beginning of which coincides with the projection of the beginning, and the end - with the projection of the end of the vector.

The projection of the vector onto the axis l called the number

,

equal to the length of the component vector on this axis, taken with a plus sign, if the direction of the components coincides with the direction of the axis l, and with a minus sign if these directions are opposite.

Basic properties of vector projections on the axis:

1. The projections of equal vectors on the same axis are equal to each other.

2. When multiplying a vector by a number, its projection is multiplied by the same number.

3. The projection of the sum of vectors on any axis is equal to the sum of the projections of the summands of the vectors on the same axis.

4. The projection of the vector onto the axis is equal to the product of the length of the projected vector by the cosine of the angle between the vector and the axis:

.

Solution. Project vectors onto an axis l as defined in the theoretical background above. It is obvious from Fig. 5a that the projection of the sum of vectors is equal to the sum of the projections of vectors. We calculate these projections:

Find the final projection of the sum of vectors:

Relationship of a vector with a rectangular Cartesian coordinate system in space

Acquaintance with a rectangular Cartesian coordinate system in space took place in the corresponding lesson, it is desirable to open it in a new window.

In an ordered coordinate system 0xyz axis Ox called abscissa, axis 0y – y-axis, and the axis 0z – axis applicate.

With an arbitrary point M space we associate vector

called radius vector points M and project it onto each of the coordinate axes. Let us denote the values ​​of the corresponding projections:

Numbers x, y, z are called coordinates of point M, respectively abscissa, ordinate and applicate, and are written as an ordered dot of numbers: M (x; y; z)(fig. 6).

A vector of unit length, the direction of which coincides with the direction of the axis, is called unit vector(or orthom) axis. Let us denote by

Accordingly, the unit vectors of the coordinate axes Ox, Oy, Oz

Theorem. Any vector can be expanded along the unit vectors of the coordinate axes:

(2)

Equality (2) is called the expansion of the vector along the coordinate axes. The coefficients of this expansion are the projections of the vector onto the coordinate axes. Thus, the coefficients of expansion (2) of the vector along the coordinate axes are the coordinates of the vector.

After choosing a certain coordinate system in space, the vector and the triplet of its coordinates uniquely determine each other, so the vector can be written in the form

Representations of the vector in the form (2) and (3) are identical.

Collinearity condition for vectors in coordinates

As we have already noted, vectors are called collinear if they are related by the relation

Let vectors ... These vectors are collinear if the coordinates of the vectors are related by the relation

,

that is, the coordinates of the vectors are proportional.

Example 6. Given vectors ... Are these vectors collinear?

Solution. Let's find out the ratio of the coordinates of these vectors:

.

The coordinates of the vectors are proportional, therefore, the vectors are collinear, or, which is the same, parallel.

Vector length and direction cosines

Due to the mutual perpendicularity of the coordinate axes, the length of the vector

is equal to the length of the diagonal of a rectangular parallelepiped built on vectors

and is expressed by the equality

(4)

The vector is completely defined by specifying two points (start and end), so the coordinates of the vector can be expressed in terms of the coordinates of these points.

Let, in a given coordinate system, the origin of the vector be at the point

and the end is at the point

From equality

Follows that

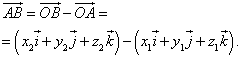
or in coordinate form

Hence, the coordinates of the vector are equal to the differences of the coordinates of the same name of the end and the beginning of the vector ... Formula (4) in this case takes the form

The direction of the vector is determined by direction cosines ... These are the cosines of the angles that the vector forms with the axes Ox, Oy and Oz... Let us denote these angles respectively α , β and γ ... Then the cosines of these angles can be found by the formulas

Directional cosines of a vector are also the coordinates of the unit vector of this vector and, thus, the vector vector

.

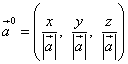
Considering that the length of the vector unit is equal to one unit, that is,

,

we obtain the following equality for the direction cosines:

Example 7. Find the length of a vector x = (3; 0; 4).

Solution. The length of the vector is

Example 8. Points are given:

Find out if the triangle built on these points is isosceles.

Solution. Using the formula for the length of the vector (6), we find the lengths of the sides and establish whether there are two equal ones among them:

Two equal sides were found, therefore there is no need to look for the length of the third side, and the given triangle is isosceles.

Example 9. Find the length of a vector and its direction cosines if .

Solution. Vector coordinates are given:

.

The length of the vector is square root from the sum of the squares of the coordinates of the vector:

.

Find the direction cosines:

Solve the vector problem yourself and then see the solution

Operations on vectors specified in coordinate form

Let there be given two vectors and, given by their projections:

Let's indicate the actions on these vectors.

Date Created: 2009-04-11 15:25:51
Last edited: 2012-02-08 09:19:45

For a long time I did not want to write this article - I was thinking how to present the material. You also need to draw pictures. But, you see, the stars have successfully formed today and there will be an article about vectors. Although, this is just a rough draft. In the future, I will split this article into several separate ones - there is enough material. Also, the article will gradually improve: I will make changes to it. in one sitting it will not be possible to reveal all aspects.

Vectors were introduced to mathematics in the nineteenth century to describe quantities that were difficult to describe using scalar values.

Vectors are used extensively in the development of computer games. They are used not only traditionally - to describe such quantities as strength or speed, but also in areas that seem to have nothing to do with vectors: storing color, creating shadows.

Scalars and vectors

First, let me remind you what a scalar is and how it differs from a vector.

Scalar values ​​store some quantity: mass, volume. That is, it is an entity that is characterized by only one number (for example, the amount of something).

A vector, unlike a scalar, is described using two values: magnitude and direction.

An important difference between vectors and coordinates: vectors are not tied to a specific location! Once again, the main thing in a vector is length and direction.

A vector is denoted by a bold letter of the Latin alphabet. For example: a, b, v.

In the first figure, you can see how the vector is designated on the plane.

Vectors in space

In space, vectors can be expressed using coordinates. But first you need to introduce one concept:

Point radius vector

Take some point M (2,1) in space. The radius vector of a point is a vector that starts at the origin and ends at the point.

We have nothing more than a vector here OM... Vector start coordinates (0,0), end coordinates (2,1). We denote this vector as a.

In this case, the vector can be written as follows a = <2, 1>... This is the coordinate form of the vector a.

The coordinates of a vector are called its components relative to the axes. For example, 2 is a vector component a about the x-axis.

Let's take another look at what point coordinates are. The coordinate of a point (for example, x) is the projection of a point onto an axis, i.e. the base of the perpendicular dropped from a point onto an axis. In our example, 2.

But back to the first picture. We have here two points A and B. Let the coordinates of the points be (1,1) and (3,3). Vector v in this case can be denoted as follows v = <3-1, 3-1>... A vector lying in two points in three-dimensional space will look like this:

v =

I think there are no difficulties here.

Multiplying a vector by a scalar

A vector can be multiplied by scalar values:

k v = =

This multiplies the scalar value with each component of the vector.

If k> 1, then the vector will increase, if k is less than one, but more than zero, the vector will decrease in length. If k is less than zero, then the vector will change direction.

Unit vectors

Unit vectors are vectors whose length is equal to one. Notice the vector with coordinates<1,1,1>will not be equal to one! Finding the length of the vector is described below in the text.

There are so-called unit vectors - these are unit vectors, which coincide in direction with the coordinate axes. i- unit vector of the x-axis, j- unit vector of the y-axis, k is the unit vector of the z axis.

Wherein i = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

Now we know what multiplication of a vector by a scalar is and what unit vectors are. Now we can write v in vector form.

v= v x i+ v y j+ v z k, where v x, v y, v z are the corresponding components of the vector

Vector addition

To fully understand the previous formula, you need to understand how vector addition works.

Everything is simple here. Take two vectors v1 = and v 2 =

v 1 + v 2 =

We are just adding the corresponding components of the two vectors.

The difference is calculated in the same way.

This is with regard to the mathematical form. For completeness, it is worth considering how addition and subtraction of vectors will look like graphically.

To add two vectors a+b... You need to match the beginning of the vector b and end of vector a... Then, between the beginning of the vector a and the end of the vector b draw a new vector. For clarity, see the second figure (letter "a").

To subtract vectors, you need to combine the beginnings of two vectors and draw a new vector from the end of the second vector to the end of the first. The second picture (letter "b") shows how it looks.

Vector length and direction

Let's look at the length first.

Length is the numerical value of the vector, excluding direction.

The length is determined by the formula (for a three-dimensional vector):

the square root of the sum of the squares of the vector components.

A familiar formula, isn't it? In general, this is the formula for the length of a segment

The direction of the vector is determined by the direction cosines of the angles formed between the vector and the coordinate axes. To find the direction cosines, the corresponding components and length are used (the picture will be later).

Representing vectors in programs

There are various ways to represent vectors in programs. Both with the help of ordinary variables, which is not efficient, and with the help of arrays, classes and structures.

Float vector3 = (1,2,3); // array for storing a vector struct vector3 // structure for storing vectors (float x, y, z;);

The greatest possibilities for storing vectors are provided by classes. In classes, we can describe not only the vector itself (variables), but also vector operations (functions).

Dot product of vectors

There are two types of vector multiplication: vector and scalar.

A distinctive feature of the dot product is that the result will always be a scalar value, i.e. number.

Here it is worth paying attention to the following point. If the result of this operation is zero, then the two vectors are perpendicular - the angle between them is 90 degrees. If the result is greater than zero, the angle is less than 90 degrees. If the result is less than zero, the angle is greater than 90 degrees.

This operation is represented by the following formula:

a · b= a x * b x + a y * b y + a z * b z

The dot product is the sum of the products of the corresponding components of two vectors. Those. Take x "s of two vectors, multiply them, then add them with the product of y" s, and so on.

Vector product of vectors

The vector product of two vectors will result in a vector perpendicular to these vectors.

a x b =

We will not discuss this formula in detail yet. Plus, it's pretty hard to memorize. We will come back to this point after getting acquainted with the determinants.

Well, for general development, it is useful to know that the length of the resulting vector is equal to the area of ​​the parallelogram built on vectors a and b.

Vector normalization

A normalized vector is a vector whose length is one.

The formula for finding the normalized vector is as follows - all components of the vector must be divided by its length:

v n = v/ | v | =

Afterword

As you've probably seen, vectors are not difficult to understand. We've covered a number of vector operations.

In the next articles of the "mathematics" section, we will discuss matrices, determinants, systems linear equations... This is all theory.

After that, we will look at matrix transformations. It is then that you will understand how important mathematics is in creating computer games. This topic will just become a practice for all the previous topics.