Creative work "Application of a peak formula". Geometry

Pick formula

1. Introduction

2. Peak formula. Proof I.

Proof II.

Proof Sh.

3. Tasks.

4. The formula of the polygon area through the coordinates of the vertices.

5. Tasks.

6. Literature

Peak formula.

1. Introduction.

In the story we draw wisdom,

in poetry - wit,

in mathematics - insight.

F. Bacon

The plot will unfold on the usual piece of checkered paper.

The lines walking on the sides of the cells form a grid, and the vertices of the cells are nodes of this grid. We draw a polygon on the sheet with the vertices in the nodes and find its area.

You can search for it in different ways. For example, you can cut a polygon on fairly simple figures, find them area and fold.

But here we are waiting for a lot of trouble. The figure is easily divided into rectangles, trapezoids, and triangles, and its area is calculated without effort.

Although the polygon looks simple enough, to calculate its area will have to be pretty hard. And if a polygon looked more bizarre? It turns out that the area of \u200b\u200bpolygons, the vertices of which are located in the grid nodes, can be calculated much simpler: there is a formula that connects them area with the number of nodes lying inside and on the border of the polygon. This wonderful and simple formula is called a peak formula.

2. Peak formula.

The tops of the polygon (not necessarily convex) are located in the nodes of the integer lattice. Inside it lies in the grid nodes, and at the border of the nodes. We prove that its area is equal to + - 1 (peak formula).

Proof I.

Consider a polygon whose vertices are in the nodes of an integer grid, that is, have integer coordinates.

The polygon will break on triangles with vertices in grid nodes that do not contain nodes either inside or on the sides.

Denote:

n. - the number of parties of the polygon,

m. - the number of triangles with vertices in grid nodes that do not contain nodes either inside or on the sides,

B - the number of nodes inside the polygon,

M is the number of nodes on the sides, including vertices.

The area of \u200b\u200ball these triangles is the same and equal.

Consequently, the polygon area is equal to
.

180 0 m. .

Now find this amount in another way.

The sum of the angles with a vertex in any internal node is 360 0.

Then the sum of the angles with the vertices in all internal nodes is 360 0 V.

The total amount of angles at nodes on the sides, but not in the vertices is 180 0 (g - n.).

The sum of the angles at the tops of the polygon is 180 0 ( n. – 2) .

The total amount of the angles of all triangles is equal 360 0 in + 180 0 (g - n.) + 180 0 (n. – 2).

Thus, 180 0 m. \u003d 360 0 in + 180 0 (g - n.) + 180 0 (n. – 2),

180 0 m. \u003d 360 0 in + 180 0 g - 180 0 n. + 180 0 n. - 180 0 · 2,

180 0 m. \u003d 360 0 in + 180 0 g - 360 0,

\u003d B +. – 1 ,

where do I get an expression for a polygon s area:

S.\u003d B +. – 1 ,

known as a peak formula.

Figure: B \u003d 24, g \u003d 9, therefore,S. = 24 + – 1 = 27,5.

Find the area of \u200b\u200bthe first polygon according to the peak formula:

B \u003d 28 (green dots);

R \u003d 20 (blue dots).

We get s \u003d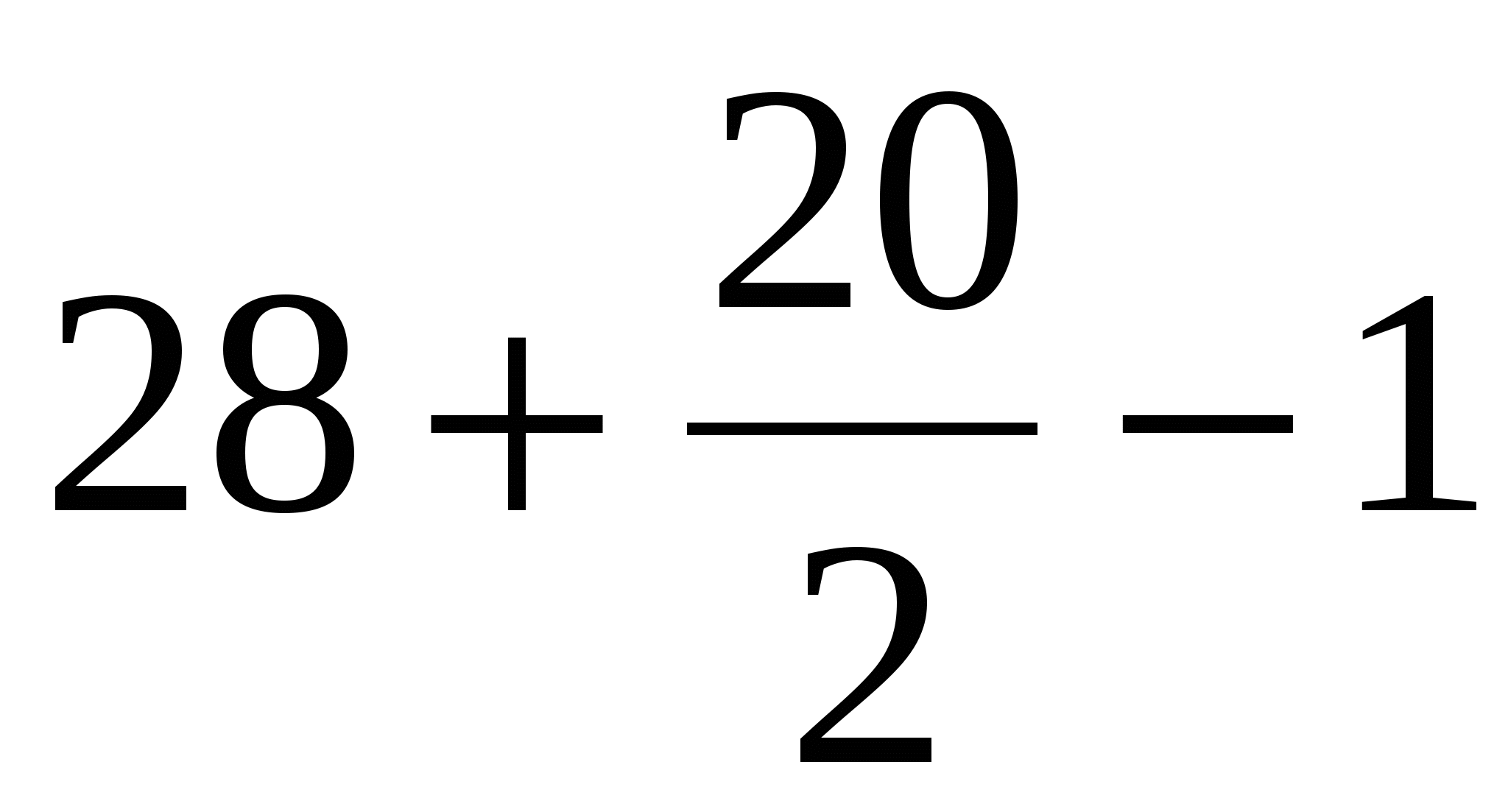
\u003d 37 sq. M.

Proof II.

Each polygon M with vertices in the nodes of an integer lattice put in accordance with the number F (M) \u003d
where the summation is carried out on all the grid nodes belonging to M, and the angle Determined as follows: =
For the inner point of the polygon, =
for a boundary point other than the top and - angle at the top, if this node is a vertex. It is easy to see that f (M) \u003d
+
\u003d B +. - 1. It remains to verify that the number F (M) is equal to the area of \u200b\u200bthe polygon M.

Let the polygon m be cut into polygons M 1 and M 2 with vertices in the grid nodes. Then f (m) \u003d f (m 1) + f (m 2), because for each node, the angles are folded. Therefore, if the peak formula is correct for two of the polygons M, M 1 and M 2, then it is true for the third.

If M is a rectangle with the sides p. and q.directed along the lattice lines

f (m) \u003d (p - 1) (Q - 1) +
\u003d PQ.

In this case, the peak formula is valid. By cutting a rectangle M diagonal on triangles M 1 and M 2 and using the fact that F (M) \u003d F (M 1) + F (M 2) and F (M 1) \u003d F (M 2), it is easy to prove the fairness of the peak formula For any rectangular triangle with customs directed along the lattice lines. I cut off a few such triangles from the rectangle, you can get any triangle.

To complete the proof of the peak formula, it remains to notice that any polygon can be cut into triangles with non-intersecting diagonals.

Proof Sh.

The relationship between the shape area and the number of nodes falling into this figure is particularly clearly visible in the case of a rectangle.

Let be Abcd. - Rectangle with vertices in the nodes and sides, walking along the grid lines.

Denote by INthe number of nodes lying inside the rectangle, and through G. - Number of nodes at its border. Move the grid on the floor of the cell to the right and the shelter down.

Then the area of \u200b\u200bthe rectangle can "distribute" between the nodes as follows: each of INnodes "controls" a whole cell of the displaced grid, each of G. - 4 boundary non-burning nodes - half of the cell, and each of the angular points is a quarter of the cell. Therefore, the area of \u200b\u200bthe rectangle s is equal

So, for rectangles with vertices in the nodes and parties going on the grid lines, we installed the formula

We prove that this formula is true not only for rectangles, but also for arbitrary polygons with vertices in the grid nodes.

Denote by S. m. polygon areaM. with vertices in nodes, and throughP m. - magnitude
whereIN m. - number of nodes insideM, but G. m. - the number of nodes on the border. Then the peak formula can be written as
.

Proof of the formula to break a few steps.

Step 1.

If a polygonM. with vertices in the nodes of the mesh cut into 2 polygonsM. 1 and M. 2 , also having tops only in the grid nodes, then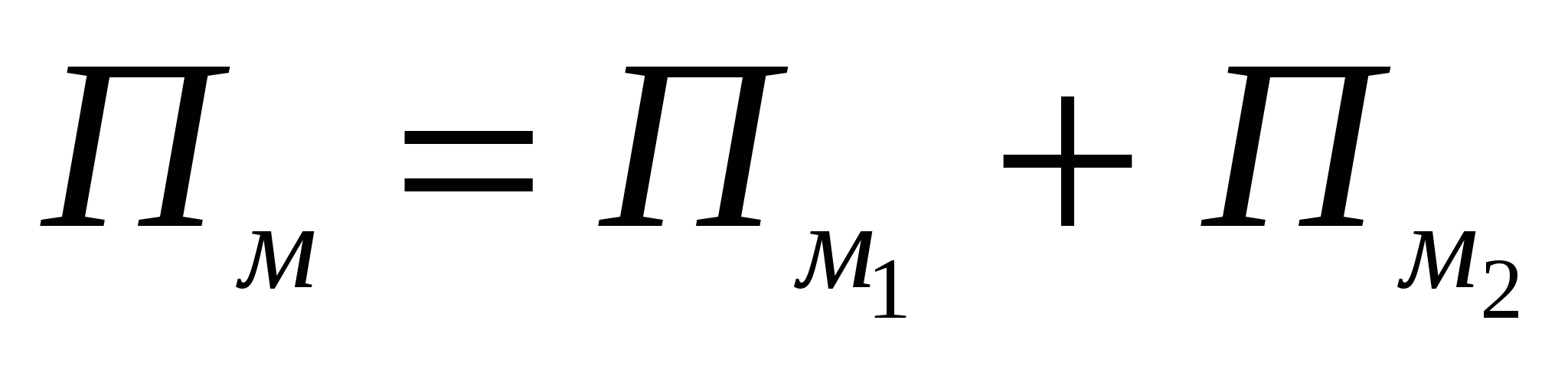
. Let a polygonM. cut into polygonsM. 1 and M. 2 with vertices in nodes segmentAv. All nodes, except those that fall on the cutAB give the same contribution to the left and right of the formula. Consider the nodes lying on the segment of AV.

If such a node lies between a and in (for example, c), then for a polygonM. it is internal, and for polygonsM. 1 and M. 2 - border. So his contribution toP m. equal to 1, and in each of the expressions
and
- 0.5, that is, the contributions of this node inP m. and
equal.

Consider the nodes A and V. They are boundary as for M.and for M. 1 , M. 2 .

Therefore, the contribution of each of these nodes inP m. equal to 0.5 and in
- unity. So, the total contribution of nodes A and BP m. equal to 1, which is 1 less than their contribution to
. But
, but .

From the general "contribution" of all nodes P m. subtracted 1, and from
Remove 2, and this compensates for the difference in the contributions of nodes A and V.

So,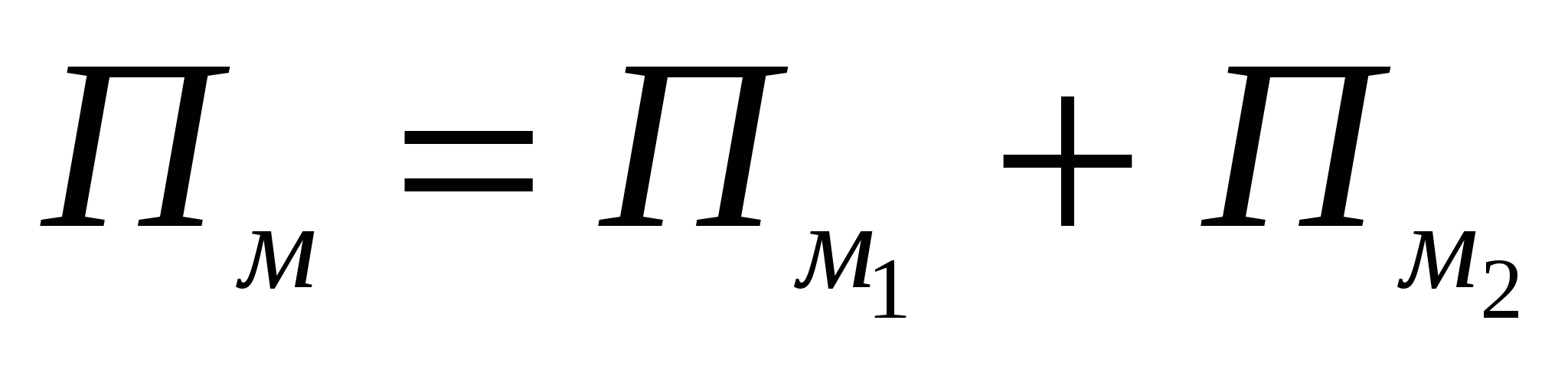
.

Step 2.

If a polygon M.with vertices in the nodes of the mesh cut into two polygons M. 1 and M. 2 (also with vertices in nodes) and the formula is true for some of the two polygons M, M. 1 , M. 2 , then it is true for the third polygon.

Let, for example, it is true forM. 1 and M. 2 , i.e
. Then (at first step), but on first step) the last expression is equalP m. , and equality
And there is a peak formula.

Step 3.

We prove the peak formula for a rectangular triangle with vertices in grid nodes and customers lying on the grid lines.

Triangle ABC Throw to rectangle Abcd. .

For rectangles, the peak formula is correct: S. Abcd. \u003d P. Abcd. . According to the first step P Abcd. \u003d P. ABC + P. ACD. , P ABC \u003d P. ACD. , so that P Abcd. \u003d 2p. ABC . But S. Abcd. = 2 S. ABC . therefore S. ABC \u003d P. ABC .

Step 4.

The peak formula is correct for an arbitrary triangle with vertices in the grid nodes.

Having considered the drawing, it is easy to understand: any such triangle can be obtained, "cutting off" from some rectangle with the sides moving along the grid lines, several rectangles and rectangular triangles with customs on the grid lines. And since the peak formula is true for rectangles and rectangular triangles, then (remember step 2) it is true for the original triangle.

We have proven that if a polygon can be cut into triangles with vertices in the grid nodes, then the peak formula is true for it.

3. Tasks.

Find the squares of the figures:

1
.

B \u003d 9.

R \u003d 4.

B \u003d 9.

R \u003d 5.

1

Hibadullina G.I. (Nurlat, Maou School No. 1)

1. Boynyovich E.A., Dorofeyev G.V., Suvorova S.B. and others. mathematics. Arithmetic. Geometry. Grade 5: Educational. For general education. organizations with adj. on an electron. The carrier -3-e ed. - M.: Enlightenment, 2014. - 223, p. : IL. - (spheres).

2. Boynyovich E.A., Kuznetsova L.V., Minaeva S.S. and others. mathematics. Arithmetic. Geometry. Grade 6: EDUCATION. For general education. organizations. 5th ed. - M.: Enlightenment, 2016. - 240 s.: Il. - (spheres).

3. Vasilyev N.B. Around the formula of the peak // Kvant. - 1974. - №2. - P. 39-43.

4. Rosets V.V. Tasks for planimetry. 5th ed., Act. and add. - M.: 2006. - 640 p.

5. Yashchenko I.V. OGE. Mathematics: Typical examinations: O-39 36 options - M.: Publishing House "National Education", 2017. - 240 s. - (OGE. FIPIX - SCHOOL).

6. I decorate OGE: mathematics. Teaching system Dmitry Gushchina. OGE-2017: tasks, answers, solutions [Electronic resource]. - Access mode: https://oge.sdamgia.ru/test?id\u003d6846966 (Date of appeal 04/02/2017).

I am a grade 6 student. He began to study geometry since last year, because I do in school on the textbook "Mathematics. Arithmetic. Geometry "edited by E.A. Binaovich, L.V. Kuznetsova, S.S. Minaeva and others.

The themes of the "Square of Figures" were attracted the greatest attention, "compilation of formulas." I noticed that the area of \u200b\u200bthe same figures can be found in various ways. In everyday life, we often encounter the tasks of finding the area. For example, find the floor area that will have to paint. Curiously because to buy the required number of wallpaper for repair, you need to know the size of the room, i.e. Square walls. The calculation of the square of the square, the rectangle and the rectangular triangle did not cause me difficulties.

Interested in this topic, I began to look for an additional material on the Internet. As a result of the search, I came across the peak formula is a formula for calculating the polygon area drawn on the checkered paper. Calculation of the area for this formula seemed to me available to any student. That is why I decided to conduct research work.

Relevance of the topic. This topic is a supplement and deepening of the study of the geometry course.

The study of this topic will help better prepare for the Olympiads and Exams.

Purpose of work:

1. Get acquainted with the formula of the peak.

2. Send the methods of decisions of geometric problems using the peak formula.

3. Systematize and summarize theoretical and practical materials.

Research tasks:

1. Check the effectiveness and feasibility of applying the formula when solving tasks.

2. Learn to apply a peak formula in tasks of different complexity.

3. Compare tasks solved using the peak formula and in the traditional way.

Main part

Historical reference

Georg Alexander Peak - Austrian Mathematics, born on August 10 of the year. He was a gifted child, his father was taught, headed by a private institution. At 16, Georg graduated from school and entered the University of Vienna. At the age of 20 received the right to teach physics and mathematics. Worldwide fame brought a formula to determine the area of \u200b\u200bthe lattice of the polygons. He published his formula in the article in 1899. She became popular when the Polish scientist Hugo Steinhuz included it in 1969 into the publication of mathematical shots.

Georg Peak was educated at the University of Vienna and defended his candidate in 1880. After receiving a doctoral degree, he was appointed assistant to Ernest Mach in Sher Ferdinanand University in Prague. He also became a teacher. He stayed in Prague to his resignation in 1927, and then returned to Vienna.

Peak was headed by the Committee in the German University of Prague, who appointed Einstein by Professor of the Department of Mathematical Physics in 1911.

He was elected a member of the Czech Academy of Sciences and Arts, but was excluded after capturing the Nazis Prague.

When the Nazis entered Austria on March 12, 1938, he returned to Prague. In March 1939, the Nazis invaded Czechoslovakia. On July 13, 1942, the peak was deported to the Teresyienstadt camp created by the Nazis in the National Czech Republic, where he died two weeks later at the age of 82 years.

Research and proof

I started my research work with finding out the question: what figures can I find the square? Create a formula for calculating the area of \u200b\u200bvarious triangles and quadrangles I could. But what about five-, six, and in general with polygons?

During the study on various sites, I saw solutions to the tasks for calculating the area of \u200b\u200bfive-, six-, and other polygons. A formula that allows you to solve these tasks, called the peak formula. It looks like this: s \u003d b + g / 2-1, where in the number of nodes lying inside the polygon, G is the number of nodes lying on the border of the polygon. The peculiarity of this formula is that it can be used only for polygons drawn on the checkered paper.

Any such polygon is easy to split into triangles with tops in grille nodes that do not contain nodes either inside or on the sides. It can be shown that the area of \u200b\u200ball these triangles is the same and equal to ½, and consequently, the polygon area is equal to half of their number T.

To find this number, denote by N the number of parties of the polygon, through the number of nodes inside it, through G is the number of nodes on the sides, including vertices. The total amount of the angles of all triangles is 180 °. T.

Now we will find the amount in another way.

The sum of the angles with a vertex in any internal node is 2.180 °, i.e. The total amount of the corners is 360 °. IN; The total amount of angles at nodes on the sides, but not in the vertices equal to (g - n) 180 °, and the sum of the angles at the tops of the polygon will be equal to (M - 2) 180 °. Thus, T \u003d 2.180 °. B + (Mr.) 180 ° + (N-2) 180 °. By opening the brackets and dividing 360 °, we obtain a formula for a polygon area, known as a peak formula.

Practical part

This formula decided to check on the tasks from the OGE-2017 collection. Took the task of calculating the area of \u200b\u200bthe triangle, quadrangle and pentagon. I decided to compare the answers, solving in two ways: 1) supplied the figures to the rectangle and from the area of \u200b\u200bthe rectangle obtained, the area of \u200b\u200brectangular triangles was deducted; 2) Applied the peak formula.

S \u003d 18-1.5-4.5 \u003d 12 and S \u003d 7 + 12 / 2-1 \u003d 12.

S \u003d 24-9-3 \u003d 12 and S \u003d 7 + 12 / 2-1 \u003d 12.

S \u003d 77-7.5-12-4.5-4 \u003d 49 and S \u003d 43 + 14/2-1 \u003d 49.

Comparing the obtained, conclude that both formulas give the same answer. Find the area of \u200b\u200bthe figure in the formula of the peak turned out to be faster and easier, because the calculations were less. Ease of solving and saving time on calculations will be useful to me in the future when the OGE is delivered.

It pushed me to check the possibility of using the peak formula on more complex figures.

S \u003d 0 + 4/2 -1 \u003d 1

S \u003d 5 + 11/2-1 \u003d 9.5

S \u003d 4 + 16/2-1 \u003d 1

Conclusion

The peak formula is simple in understanding and convenient to use. First, it is enough to be considered to be considered, divide on 2, fold and deduct. Secondly, you can find an area and a complex figure, without spending a lot of time. Thirdly, this formula works for any polygon.

The disadvantage is that the peak formula is applicable only for figures that are drawn on the checkered paper and the vertices lie on the nodes of the cells.

I am sure that when surrendering the final exams, the tasks for calculating the area of \u200b\u200bfigures will not cause difficulties. After all, I'm already familiar with the formula of peak.

Bibliographic reference

Gabbazov N.N. Peak formula // Start in science. - 2017. - № 6-1. - p. 130-132;
URL: http://science-start.ru/ru/Article/View?id\u003d908 (date of handling: 03/05/2020).

The text of the work is placed without images and formulas.
The full version of the work is available in the "Work Files" tab in PDF format

Introduction

I, student grade 6. He began to study geometry since last year, because I do in school on the textbook "Mathematics. Arithmetic. Geometry "edited by E.A. Binaovich, L.V. Kuznetsova, S.S. Minaeva and others.

The themes of the "Square of Figures" were attracted the greatest attention, "compilation of formulas." I noticed that the area of \u200b\u200bthe same figures can be found in various ways. In everyday life, we often encounter the tasks of finding the area. For example, find the floor area that will have to paint. Curiously because to buy the required number of wallpaper for repair, you need to know the size of the room, i.e. Square walls. The calculation of the square of the square, the rectangle and the rectangular triangle did not cause me difficulties.

Interested in this topic, I began to look for an additional material on the Internet. As a result of the search, I came across the peak formula is a formula for calculating the polygon area drawn on the checkered paper. Calculation of the area for this formula seemed to me available to any student. That is why I decided to conduct research work.

Relevance of the topic:

This topic is a supplement and deepening of the study of the geometry course.

The study of this topic will help better prepare for the Olympiads and Exams.

Purpose of work:

Get acquainted with the formula of the peak.

Send the techniques of geometric tasks using the peak formula.

Systematize and summarize theoretical and practical materials.

Research tasks:

Check the effectiveness and feasibility of using the formula when solving tasks.

Learn to apply a peak formula in tasks of different complexity.

Compare tasks solved using the peak formula and in the traditional way.

Main part

1.1. Historical reference

Georg Alexander Peak - Austrian Mathematician, was born on August 10, 1859. He was a gifted child, his father was taught, headed by a private institution. At 16, Georg graduated from school and entered the University of Vienna. At the age of 20 received the right to teach physics and mathematics. Worldwide fame brought a formula to determine the area of \u200b\u200bthe lattice of the polygons. He published his formula in the article in 1899. She became popular when the Polish scientist Hugo Steinhuz included it in 1969 into the publication of mathematical shots.

Georg Peak was educated at the University of Vienna and defended his candidate in 1880. After receiving a doctoral degree, he was appointed assistant to Ernest Mach in Sher Ferdinanand University in Prague. He also became a teacher. He stayed in Prague to his resignation in 1927, and then returned to Vienna.

Peak was headed by the Committee in the German University of Prague, who appointed Einstein by Professor of the Department of Mathematical Physics in 1911.

He was elected a member of the Czech Academy of Sciences and Arts, but was excluded after capturing the Nazis Prague.

When the Nazis entered Austria on March 12, 1938, he returned to Prague. In March 1939, the Nazis invaded Czechoslovakia. On July 13, 1942, the peak was deported to the Teresyienstadt camp created by the Nazis in the National Czech Republic, where he died two weeks later at the age of 82 years.

1.2. Research and proof

I started my research work with finding out the question: what figures can I find the square? Create a formula for calculating the area of \u200b\u200bvarious triangles and quadrangles I could. But what about five-, six, and in general with polygons?

During the study on various sites, I saw solutions to the tasks for calculating the area of \u200b\u200bfive-, six-, and other polygons. A formula that allows you to solve these tasks, called the peak formula. She looks like this: s \u003d B + g / 2-1where IN - the number of nodes lying inside the polygon, G.- the number of nodes lying on the border of the polygon. The peculiarity of this formula is that it can be used only for polygons drawn on the checkered paper.

Any such polygon is easy to split into triangles with tops in grille nodes that do not contain nodes either inside or on the sides. It can be shown that the area of \u200b\u200ball these triangles is the same and equal to ½, and consequently, the polygon area is equal to half of their number T.

To find this number, denote by n the number of parties of the polygon, through IN- the number of nodes inside it, through G.- The number of nodes on the sides, including vertices. The total amount of the angles of all triangles is 180 °. T.

Now we will find the amount in another way.

The sum of the angles with a vertex in any internal node is 2.180 °, i.e. The total amount of the corners is 360 °. IN;the total amount of angles at nodes on the sides, but not at the vertices is equal to ( G- n) 180°, and the sum of the corners at the tops of the polygon will be equal to ( G- 2) 180°. In this way, T \u003d.2.180 °. B + (Mr.) 180° + (n -2)180 °. By opening the brackets and dividing 360 °, we obtain a formula for a polygon area, known as a peak formula.

2. Practical part

This formula decided to check on the tasks from the OGE-2017 collection. Took the task of calculating the area of \u200b\u200bthe triangle, quadrangle and pentagon. I decided to compare the answers, solving in two ways: 1) supplied the figures to the rectangle and from the area of \u200b\u200bthe rectangle obtained, the area of \u200b\u200brectangular triangles was deducted; 2) Applied the peak formula.

S \u003d 18-1.5-4.5 \u003d 12 and S \u003d 7 + 12 / 2-1 \u003d 12

S \u003d 24-9-3 \u003d 12 and S \u003d 7 + 12 / 2-1 \u003d 12

S \u003d 77-7.5-12-4.5-4 \u003d 49 and S \u003d 43 + 14/2-1 \u003d 49

Comparing the obtained, conclude that both formulas give the same answer. Find the area of \u200b\u200bthe figure in the formula of the peak turned out to be faster and easier, because the calculations were less. Ease of solving and saving time on calculations will be useful to me in the future when the OGE is delivered.

It pushed me to check the possibility of using the peak formula on more complex figures.

S \u003d 0 + 4/2 -1 \u003d 1

S \u003d 5 + 11/2-1 \u003d 9.5

S \u003d 4 + 16/2-1 \u003d 1

Conclusion

The peak formula is simple in understanding and convenient to use. First, it is enough to be considered to be considered, divide on 2, fold and deduct. Secondly, you can find an area and a complex figure, without spending a lot of time. Thirdly, this formula works for any polygon.

The disadvantage is that the peak formula is applicable only for figures that are drawn on the checkered paper and the vertices lie on the nodes of the cells.

I am sure that when surrendering the final exams, the tasks for calculating the area of \u200b\u200bfigures will not cause difficulties. After all, I'm already familiar with the formula of peak.

Bibliography

Binaovich E.A., Dorofeyev G.V., Suvorova S.B. and others. mathematics. Arithmetic. Geometry. Grade 5: Educational. For general education. organizations with adj. on an electron. The carrier -3-e ed.-M.: Enlightenment, 2014.- 223, p. : IL. - (spheres).

Baynovich E.A., Kuznetsova L.V., Minaeva S.S. and others. mathematics. Arithmetic. Geometry. Grade 6: EDUCATION. For general education. Organizations - 5th ed.-M.: Enlightenment, 2016.-240c. : IL.- (spheres).

Vasilyev N.B. Around the formula of the peak. //Kvant.- 1974.-№2. -C.39-43

Rosets V.V. Tasks for planimetry. / 5- ed., Act. And add. - M.: 2006.-640С.

I.V. Yashchenko. Mathematics: typical exam options: O-39 36 options - M.: Publishing House "National Education", 2017. -240 p. - (OGE. Phi-school).

"I solved OGE": mathematics. Teaching system Dmitry Gushchina. OGE-2017: tasks, answers, solutions [Electronic resource]. Access mode: https://oge.sdamgia.ru/test?id\u003d6846966 (Date of appeal 04/02/2017)

Draw some polygon on the checkered paper. For example, such as shown in Figure 1.

Let's try to calculate its area. How to do it? Probably the easiest to break it on rectangular triangles And rectangles whose areas are already easy to calculate and fold the results obtained. Used by me is simple, but very cumbersome, in addition, it is not suitable for any polygons.

Consider a nondegenerate simple integer polygon (i.e., it is connected - any two points can be connected by a continuous curve, entirely in it is contained, and all of its vertices have whole coordinates, its border is a coherent broken without self-intersection, and it has a nonzero area). To calculate the area of \u200b\u200bsuch a polygon, you can use the following theorem:

Peak theorem. Let - the number of integer points inside the polygon - the number of integer points at its border - its area. Then valid pick formula:

Example. For a polygon in Figure 1 (yellow dots), (blue dots, do not forget about the vertices!), Therefore, square units.

Proof of peak theorem. First, we note that the peak formula is valid for a single square. Indeed, in this case we have and

Consider a rectangle with the sides lying on the lattice lines. Let the length of his sides are equal and. We have in this case, according to the peak formula,

We now consider a rectangular triangle with customers lying on the coordinate axes. Such a triangle is obtained from a rectangle with the parties and, considered in the previous case, cutting it on the diagonal. Let the diagonals lie integer points. Then for this occasion and we get that

Now consider an arbitrary triangle. It can be obtained by cutting off several rectangular rectangles from the rectangle and possibly a rectangle (see Figures 2 and 3). Since both for a rectangle, and for a rectangular triangle of the peak formula, we get that it will also be valid for an arbitrary triangle.

It remains to make the last step: go from triangles to polygons. Any polygon can be divided into triangles (for example, diagonals). Therefore, it is necessary to simply prove that when adding any triangle to an arbitrary polygon, the peak formula remains true.

Let the polygon and the triangle have a common side. Suppose that for the peak formula, we will prove that it will be correct for a polygon obtained from the addition. Since they have the overall side, then all integer points lying on this side, except for two vertices, become internal points of the new polygon. The vertices will be boundary points. Denote the number of common points through and get

The number of internal integer points of the new polygon,

The number of boundary points of the new polygon.

From these equalities we get

Since we suggested that the theorem is true for and for separately,

Thus, the peak formula is proved.

This formula was opened by Austrian Mathematics Peak Georg Alexandrov (1859 - 1943) in 1899. In addition to this formula, Georg Peak opened the peak theorem, Peak - Julia, Peak - Nevalin, proved the inequality of Schwartz - Peak. IN Appendix 1. You can see the non-standard tasks considered by me to apply the peak formula.

Pick formula

Sazhina Valery Andreevna, student 9 Class Maou "Sosh№11" G Ust-Ilimsk Irkutsk Region

Leader: Gubar Oksana Mikhailovna, Mathematics teacher of the highest qualifying category MOU "SOSH№11" Mr. Ust-Ilimsk Irkutsk region

2016 year

Introduction

When studying the topic of the geometry of the "Polygon Square", I decided to find out: Is there a way to find squares other than those that we studied in the lessons?

In this way, there is a peak formula. L. V. Gorina in "Materials for Finding Self-Education" described this formula: "Introduction to the peak formula is particularly relevant on the eve of the delivery of the USE and GIA. With this formula, you can easily solve a large class of tasks offered on the exams - these are tasks to find the area of \u200b\u200bthe polygon depicted on the checkered paper. Little peak formula will replace a whole set of formulas necessary for solving such tasks. The formula of the peak will work "one for all ..."! ".

In the materials of the exam, I met the tasks with the practical content of land plots. I decided to check whether this formula is applicable to find the area of \u200b\u200bthe school area, the city's neighborhoods, area. As well as its use is rationally to solve problems.

Object of study: Peak formula.

Research Subject: rationality Application of the peak formula when solving tasks.

The goal of the work is to substantiate the rationality of using the peak formula when solving the tasks to find the area of \u200b\u200bfigures depicted on the checkered paper.

Research methods: modeling, comparison, generalization, analogies, study of literary and Internet resources, analysis and classification of information.

Pick up the necessary literature, analyze and systematize the information obtained;

Consider various methods and techniques for solving problems on cellular paper;

Check experimentally by rationality of using the peak formula;

Consider the use of this formula.

Hypothesis: If you apply the peak formula to find the area of \u200b\u200bthe polygon, then you can find the area of \u200b\u200bthe territory, and the solution of tasks on the checkered paper will be more rational.

Main part

Theoretical part

Checkered paper (more precisely - its nodes) on which we often prefer to draw and draw, is one of the most important examples of the point lattice on the plane. Already this simple lattice served K. Gauss by the starting point for comparing the area of \u200b\u200bthe circle with the number of points with integer coordinates inside it. The fact that some simple geometric statements about the figures on the plane have deep consequences in arithmetic studies, was explicitly noticed by the city of Minkowski in 1896, when he for the first time for consideration of theoretical and numerical problems attracted geometric methods.

Draw some polygon on the checkered paper (Appendix 1, Figure 1). Let's try to calculate its area. How to do it? Probably, the easiest way to break it on rectangular triangles and a trapezium, whose area is already easy to calculate and fold the results obtained.

The method used is simple, but very cumbersome, in addition, it is not suitable for any polygons. So the next polygon cannot be broken down onto rectangular triangles, as we did it in the previous case (Appendix 2, Figure 2). You can, for example, try to add it to the "good" needed to us, that is, the area of \u200b\u200bwhich we will be able to calculate the described method, then from the resulting number of the area of \u200b\u200bthe added part.

However, it turns out that there is a very simple formula that allows you to calculate the area of \u200b\u200bsuch polygons with vertices in the nodes of the square grid.

This formula was opened by Austrian Mathematics Peak Georg Alexandrov (1859 - 1943) in 1899. In addition to this formula, Georg Peak opened the peak theorem, Peak - Julia, Peak - Nevalin, proved the inequality of Schwartz - Peak.

This formula remained unnoticed for some time after the peak published it, but in 1949 the Polish mathematician of Hugo Stengauses included the theorem in his famous "mathematical kaleidoscope". From this time, the peak theorem has become widely known. In Germany, the peak formula is included in school textbooks.

It is a classic result of combinatorial geometry and geometry of numbers.

Proof of the formula of the peak

Let the ABSD be a rectangle with vertices in the nodes and parties running along the grid lines (Appendix 3, Figure 3).

Denote by B - the number of nodes lying inside the rectangle, and through G is the number of nodes at its border. Move the grid on the poles to the right and the shelter

down. Then the area of \u200b\u200bthe rectangle can be "distributed" between the nodes as follows: each of the nodes "controls" the whole cell of the displaced grid, and each of the nodes - 4 boundary non-angular node - half of the cell, and each of the angular points is a quarter of cells. Therefore, the area of \u200b\u200bthe rectangle s is equal

S. \u003d B +. + 4 · \u003d B +. - 1 .

So, for rectangles with vertices in the nodes and parties going on the grid lines, we set the formula S \u003d B + - 1 . This is a peak formula.

It turns out that this formula is true not only for rectangles, but also for arbitrary polygons with vertices in the grid nodes.

Practical part

Finding the area of \u200b\u200bfigures by a geometric method and by peak formula

I decided to make sure that the peak formula is true for all the considered examples.

It turns out that if a polygon can be cut into triangles with vertices in the grid nodes, then it is true for it the peak formula.

I looked at some challenges on cellular paper with cells of 1 cm1 cm and spent comparative analysis By solving tasks (Table #1).

Table #1 Solving tasks in various ways.

Picture

According to the geometry formula

By peak formula

Task number 1.

S \u003d S. etc - (2s. 1 + 2s. 2 )

S. etc =4*5=20 cm 2

S. 1 =(2*1)/2=1 cm 2

S. 2 =(2*4)/2=4 cm 2

S \u003d 20- (2 * 1 + 2 * 4) \u003d 10cm 2

Answer :10 cm ².

B \u003d 8, r \u003d 6

S. \u003d 8 + 6/2 - 1 \u003d 10 (cm²)

Answer: 10 cm².

Task number 2.

a \u003d 2, H \u003d 4

S \u003d A * H \u003d 2 * 4 \u003d 8cm 2

Answer : 8 cm ².

B \u003d 6, r \u003d 6

S. \u003d 6 + 6/2 - 1 \u003d 8 (cm²)

Answer: 8 cm².

Task number 3.

S \u003d S. kv. - (S. 1 + 2s. 2 )

S. kv. =4 2 =16 cm 2

S. 1 \u003d (3 * 3) / 2 \u003d 4.5 cm 2

S. 2 \u003d (1 * 4) / 2 \u003d 2cm 2

S.\u003d 16- (4.5 + 2 * 2) \u003d 7.5 cm 2

B \u003d 6, g \u003d 5

S. \u003d 6 + 5/2 - 1 \u003d 7.5 (cm²)

Answer: 7.5 cm².

Task number 4.

S \u003d S. etc - (S. 1 + S. 2+ S. 3 )

S. etc =4 * 3=12 cm 2

S. 1 =(3*1)/2=1,5 cm 2

S. 2 =(1*2)/2=1 cm 2

S. 3 =(1+3)*1/2=2 cm 2

S \u003d 12- (1.5 + 1 + 2) \u003d 7.5cm 2

B \u003d 5, g \u003d 7

S. \u003d 5 + 7/2 - 1 \u003d 7.5 (cm²)

Answer: 7.5 cm².

Task number 5.

S \u003d S. etc - (S. 1 + S. 2+ S. 3 )

S. etc =6 * 5=30 cm 2

S. 1 =(2*5)/2=5 cm 2

S. 2 =(1*6)/2=3 cm 2

S. 3 =(4*4)/2=8 cm 2

S \u003d 30- (5 + 3 + 8) \u003d 14cm 2

Answer: 14 cm²

B \u003d 12, r \u003d 6

S. \u003d 12 + 6/2 - 1 \u003d 14 (cm²)

Answer: 14 cm²

A task №6.

S. Tr \u003d (4 + 9) / 2 * 3 \u003d 19.5 cm 2

Answer: 19.5 cm 2

B \u003d 12, g \u003d 17

S. \u003d 12 + 17/2 - 1 \u003d 19.5 (cm²)

Answer: 19.5 cm 2

A task №7. Find the area of \u200b\u200bthe forest massif (in m²) depicted on the plan with a square mesh 1 × 1 (cm) on a scale of 1 cm - 200 m

S \u003d S. 1 + S. 2+ S. 3

S. 1 =(800*200)/2=80000 m. 2

S. 2 =(200*600)/2=60000 m. 2

S. 3 =(800+600)/2*400=

280000 m. 2

S \u003d.80000+60000+240000=

420000m 2.

Answer: 420,000 m²

B \u003d 8, g \u003d 7. S. \u003d 8 + 7/2 - 1 \u003d 10.5 (cm²)

1 cm² - 200² m²; S. \u003d 40000 · 10.5 \u003d 420 000 (m²)

Answer: 420,000 m²

Task number 8. . Find the field area (in m²) depicted on the plan with a square mesh 1 × 1 (cm) on the scale

1 cm - 200 m.

S.= S. kV -2 ( S. Tr +. S. ladder)

S. kv \u003d 800 * 800 \u003d 640000 m 2

S. Tr \u003d (200 * 600) / 2 \u003d 60000m 2

S. Trap \u003d (200 + 800) / 2 * 200 \u003d

100000m 2.

S.=640000-2(60000+10000)=

320000 m 2.

Answer: 320,000 m²

Decision. Find S. The area of \u200b\u200bthe quadricle depicted on the checkered paper by peak formula:S. \u003d B + - 1

B \u003d 7, r \u003d 4. S. \u003d 7 + 4/2 - 1 \u003d 8 (cm²)

1 cm² - 200² m²; S. \u003d 40000 · 8 \u003d 320 000 (m²)

Answer: 320,000 m²

Task number 9. . Find SquareS. sectors, counting square cells equal to 1. In response, specify .

The sector is one fourth part of the circle and, therefore, its area is equal to one fourth area of \u200b\u200bthe circle. Circle area is equal to πR. 2 where R. - Circle radius. In our caseR. =√5 And, therefore, the areaS. sectors are 5π / 4. FromS./ π \u003d 1.25.

Answer. 1.25.

R \u003d 5, B \u003d 2, S. \u003d B + g / 2 - 1 \u003d 2 + 5/2 - 1 \u003d 3.5, ≈ 1,11

Answer. 1,11.

Task number 10. Find Square S. rings, counting square cells equal to 1. In response, specify .

The rings area is equal to the difference in the area of \u200b\u200bexternal and inner circles. RadiusR. exterior circle equal

2, radius r. the inner circle is 2. Consequently, the rings area is 4 And, therefore, . Answer: 4.

R \u003d 8, B \u003d 8, S. \u003d B + g / 2 - 1 \u003d 8 + 8/2 - 1 \u003d 11, ≈ 3,5

Answer: 3.5

Conclusions: The considered tasks are similar to the task from the options for measuring materials of the exam in mathematics (tasks No. 5.6),.

From the considered task decisions, I saw that some of them, such as tasks No. 2.6, it is easier to solve, applying geometric formulas, since the height and base can be defined in the figure. But most of the tasks require a splitting of the figure to a simpler (task number 7) or completing to a rectangle (Tasks No. 14,5), a square (tasks No. 3,8).

From solving problems No. 9 and No. 10, I saw that the use of a peak formula for figures that are not polygons, gives an approximate result.

In order to test the rationality of the application of the peak formula, I conducted a study for the time spent (Appendix 4, Table No. 2).

Conclusion: From the table and diagram (Appendix 4, Chart 1) it can be seen that when solving problems with the formula of the peak, time is spent much less.

Finding the area of \u200b\u200bthe spatial forms

Check the applicability of this formula to spatial forms (Appendix 5, Figure 4).

Find the area of \u200b\u200bthe full surface of the rectangular parallelepiped, counting the side of square cells equal to 1.

This is a lack of formula.

Application of the peak formula for finding the area of \u200b\u200bthe territory

Solving tasks with practical content (tasks number 7.8; Table No. 1), I decided to apply this method to find the area of \u200b\u200bour school territory, the neighborhoods of the city of Ust-Ilimsk, the Irkutsk region.

Having read the "Project of the boundaries of the land plot Mausosh№11 G. Nast-Ilimsk" (Appendix 6), I found the area of \u200b\u200bour school territory and compared with an area of \u200b\u200bland plot boundaries (Appendix 9, Table 3).

Having considered the Right Bank of Ust-Ilimsk (Appendix 7), I calculated the microdistricon area and compared with the data from the "Ust-Ilimsk" of the Irkutsk Region ". The results presented in the table (Appendix 9, Table 4).

Having considered the map of the Irkutsk region (Appendix 7), I found the area of \u200b\u200bthe territory and compared with the data from Wikipedia. The results presented in the table (Appendix 9, Table 5).

After analyzing the results, I came to the conclusion: according to the peak formula, these areas can be found much easier, but the results are approximate.

From the studies carried out, the most accurate importance I received when I find the area of \u200b\u200bthe school territory (Appendix 10, Chart 2). A larger discrepancy in the results succeeded when the Square of the Irkutsk Region (Appendix 10, Chart 3). This is due to the fact. That not all the boundaries of the region are the parties to the polygons, and the vertices are not nodal points.

Conclusion

As a result of my work, I expanded my knowledge about solving problems on the checkered paper, determined the classification of the tasks under study.

When performing the work, the tasks were solved to find the area of \u200b\u200bpolygons depicted on the checkered paper in two ways: geometric and using the peak formula.

Analysis of solutions and experiment to determine the time spent showed that the application of the formula makes it possible to solve the task of finding the area of \u200b\u200bthe polygon, more rationally. This saves time to the exam in mathematics.

Finding the area of \u200b\u200bvarious figures depicted on the checkered paper made it possible to conclude that the use of a peak formula for calculating the area of \u200b\u200bthe circular sector and the ring is impractical, as it gives an approximate result, and that the peak formula does not apply to solve problems in space.

Also in the work there were found areas of various territories by peak formula. It can be concluded: the use of the formula for finding the area of \u200b\u200bvarious territories is possible, but the results are approximate.

The hypothesis nominated by me was confirmed.

I came to the conclusion that the topic that interest me is quite multifaceted, the tasks on the checkered paper are diverse, the methods and techniques of their decisions are also diverse. Therefore, I decided to continue working in this direction.

Literature

Volkov S.D .. Project of the boundaries of the land plot, 2008, p. sixteen.

Gorina L.V., Mathematics. All for the teacher, m: science, 2013 g. No. 3, p. 28.

Prokopieva V.P., Petrov A.G., General Plan of the city of Ust-Ilimsk, Irkutsk Region, Gosstroy Russia, 2004. with. 65.

Riss E. A., Zharkovskaya N. M., Geometry of the Checkered Paper. Peak formula. - Moscow, 2009, № 17, p. 24-25.

Smirnova I. M. ,. Smirnov V. A, geometry on cellular paper. - Moscow, pure ponds, 2009, p. 120.

Smirnova I. M., Smirnov V. A., Geometric tasks with practical content. - Moscow, pure ponds, 2010, p. 150.

Objectives of the open bank tasks in mathematics FIPI, 2015.

City map of Ust-Ilimsk.

Map of the Irkutsk region.

Wikipedia.