Vektor. Əsas xüsusiyyətlər

Tərif Sıralı kolleksiya (x 1, x 2, ..., x n) n həqiqi ədəd adlanır n-ölçülü vektor, və x i (i = 1, ..., n) ədədləridir komponentlər, və ya koordinatlar,

Misal. Əgər, məsələn, müəyyən avtomobil zavodu hər növbədə 50 minik avtomobili, 100 yük maşını, 10 avtobus, minik avtomobilləri üçün 50 dəst, yük maşınları və avtobuslar üçün 150 dəst ehtiyat hissələri istehsal etməlidirsə, onda bu zavodun istehsal proqramını aşağıdakı formada yazmaq olar. beş komponentdən ibarət vektorun forması (50, 100, 10, 50, 150).

Qeyd. Vektorlar qalın kiçik hərflərlə və ya yuxarıda bar və ya ox olan hərflərlə işarələnir, məsələn, a və ya . İki vektor deyilir bərabərdirəgər onların eyni sayda komponentləri varsa və onlara uyğun komponentlər bərabərdirsə.

Vektor komponentləri dəyişdirilə bilməz, məsələn, (3, 2, 5, 0, 1) və (2, 3, 5, 0, 1) müxtəlif vektorlardır.
Vektorlar üzərində əməliyyatlar. Məhsula görəx= (x 1, x 2, ..., x n) λ həqiqi ədədinə λ vektoru deyilir. x= (λ x 1, λ x 2, ..., λ x n).

Məbləğx= (x 1, x 2, ..., x n) və y= (y 1, y 2, ..., y n) vektor adlanır x + y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

Vektorların fəzası. N-ölçülü vektor fəzası R n həqiqi ədədlərə vurma və toplama əməliyyatlarının təyin olunduğu bütün n ölçülü vektorların çoxluğu kimi müəyyən edilir.

İqtisadi illüstrasiya. n-ölçülü vektor fəzasının iqtisadi təsviri: malların sahəsi (mallar). Altında əmtəə müəyyən bir yerdə müəyyən bir zamanda satışa çıxan bəzi mal və ya xidməti başa düşəcəyik. Tutaq ki, əlində sonlu sayda əşyalar var, n; onların hər birinin istehlakçı tərəfindən satın alınan kəmiyyətləri əmtəə dəsti ilə xarakterizə olunur

x= (x 1, x 2, ..., x n),

burada x i istehlakçının aldığı i-ci əmtəənin məbləğini bildirir. Biz bütün malların ixtiyari bölünmə xüsusiyyətinə malik olduğunu fərz edəcəyik ki, onların hər birinin mənfi olmayan istənilən məbləği alınsın. Onda bütün mümkün mal dəstləri mallar məkanının vektorlarıdır C = ( x= (x 1, x 2, ..., x n) x i ≥ 0, i = 1, ..., n).

Xətti müstəqillik. Sistem e 1 , e 2 , ... , e m n-ölçülü vektorlar deyilir xətti asılıλ 1, λ 2, ..., λ m ədədləri varsa, onlardan ən azı biri sıfırdan fərqli olsun ki, λ 1 olsun. e 1 + λ m e m = 0; əks halda bu vektorlar sistemi adlanır xətti müstəqil, yəni göstərilən bərabərlik yalnız bütün λ 1 = λ 2 = ... = λ m = 0 olduqda mümkündür. Vektorların xətti asılılığının həndəsi mənası R 3, istiqamətlənmiş seqmentlər kimi şərh olunur, aşağıdakı teoremləri izah edin.

Teorem 1. Bir vektordan ibarət sistem yalnız və yalnız bu vektor sıfır olduqda xətti asılıdır.

Teorem 2. İki vektorun xətti asılı olması üçün onların kollinear (paralel) olması zəruri və kifayətdir.

Teorem 3 ... Üç vektorun xətti asılı olması üçün onların koplanar olması (eyni müstəvidə olması) zəruri və kifayətdir.

Vektorların sol və sağ üçlüyü. Üç qeyri-komplanar vektor a, b, cçağırdı sağ onların ümumi mənşəli müşahidəçi vektorların uclarını keçərsə a, b, c göstərilən ardıcıllıqla, saat əqrəbi istiqamətində görünür. Əks halda a, b, c -sol üçlü... Vektorların bütün sağ (və ya sol) üçlüyü deyilir bərabər yönümlü.

Baza və koordinatlar. Troyka e 1, e 2 , e 3 qeyri-komplanar vektor R 3 adlanır əsas, və vektorların özləri e 1, e 2 , e 3 - əsas... İstənilən vektor aəsas vektorlar baxımından unikal şəkildə genişləndirilə bilər, yəni formada təmsil olunur

a= x 1 e 1 + x 2 e 2 + x 3 e 3, (1.1)

genişlənmədə (1.1) x 1, x 2, x 3 ədədləri deyilir koordinatlarıaəsasında e 1, e 2 , e 3 və işarələnmişdir a(x 1, x 2, x 3).

Ortonormal əsas. Əgər vektorlar e 1, e 2 , e 3 cüt perpendikulyardır və hər birinin uzunluğu birə bərabərdir, onda əsas deyilir ortonormal, və koordinatları x 1, x 2, x 3 - düzbucaqlı. Ortonormal bazisin bazis vektorları ilə işarələnəcək i, j, k.

Bunu kosmosda fərz edəcəyik R 3, Dekart düzbucaqlı koordinatlarının düzgün sistemi seçilir (0, i, j, k}.

Vektor məhsulu.Vektor məhsulua vektor başına b vektor adlanır c aşağıdakı üç şərtlə müəyyən edilir:

1. Vektor uzunluğu c vektorlar üzərində qurulmuş paraleloqramın sahəsinə ədədi olaraq bərabərdir a və b, yəni.
c= | a || b | günah ( a^b).

2. Vektor c vektorların hər birinə perpendikulyar a və b.

3. Vektorlar a, b və c göstərilən qaydada sağ üçlü şəklində alınır.

Vektor məhsulu üçün c notu təqdim olunur c =[ab] və ya
c = a × b.

Əgər vektorlar a və b collinear, sonra günah ( a ^ b) = 0 və [ ab] = 0, xüsusən, [ aa] = 0. Vahid vektorların vektor hasilləri: [ ij]=k, [jk] = i, [ki]=j.

Əgər vektorlar a və bəsasında verilir i, j, k koordinatları a(a 1, a 2, a 3), b(b 1, b 2, b 3), onda

Qarışıq iş. Əgər iki vektorun çarpaz hasili a və b skalyarın üçüncü vektora vurulması c, onda üç vektorun belə hasilinə deyilir qarışıq iş və simvolu ilə işarələnir a b c.

Əgər vektorlar a, b və cəsasında i, j, k onların koordinatları ilə verilir
a(a 1, a 2, a 3), b(b 1, b 2, b 3), c(c 1, c 2, c 3), onda

.

Qarışıq məhsulun sadə həndəsi şərhi var - bu, bu üç vektor üzərində qurulmuş paralelepipedin həcminə mütləq qiymətə bərabər olan skalyardır.

Vektorlar sağ üçlük təşkil edərsə, onda onların qarışıq hasilatı göstərilən həcmə bərabər müsbət ədəddir; əgər üç a, b, c - sonra sol a b c<0 и V = - a b c, buna görə də V = |a b c |.

Birinci fəslin məsələlərində rast gəlinən vektorların koordinatlarının sağ ortonormal bazisə nisbətən verildiyi qəbul edilir. Vahid vektor vektora koordinat a, simvolu ilə işarələnir a O. Simvol r=OM M nöqtəsinin radius vektoru a, AB və ya simvolları ilə işarələnir |a |, |AB | vektorların modulları a və AB.

Misal 1.2. Vektorlar arasındakı bucağı tapın a= 2m+4n və b= m-n, harada m və n - vahid vektorlar və aralarındakı bucaq m və n 120 p-ə bərabərdir.

Həll... Bizdə: cos φ = ab/ ab, ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4 + 2cos120 o = - 2 + 2 (-0,5) = -3; a = ; a 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4 + 16 (-0,5) + 16 = 12, belə ki, a =. b = ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 = 1-2 (-0,5) +1 = 3, belə ki, b =. Nəhayət, biz var: cos φ == -1/2, φ = 120 o.

Misal 1.3. Vektorları bilmək AB(-3, -2.6) və e.ə(-2,4,4), ABC üçbucağının AD hündürlüyünün uzunluğunu hesablayın.

Həll... ABC üçbucağının sahəsini S ilə ifadə edərək, alırıq:
S = 1/2 BC. Onda AD = 2S / BC, BC = = = 6,
S = 1/2 | AB ×AC |. AC = AB + BC, belə ki, vektor AC koordinatlarına malikdir
.

TƏrif

Vektor(latdan." vektor"-" daşıyıcı ") - kosmosda və ya müstəvidə düz xəttin yönəldilmiş seqmenti.

Qrafik olaraq vektor müəyyən uzunluqda yönəldilmiş xətt seqmenti kimi təsvir edilir. Əvvəli nöqtədə, sonu isə nöqtədə olan vektor kimi işarələnir (şək. 1). Həmçinin, vektor bir kiçik hərflə işarələnə bilər, məsələn,.

Əgər koordinat sistemi fəzada göstərilibsə, onda vektor onun koordinatları toplusu ilə unikal şəkildə təyin oluna bilər. Yəni vektor dedikdə böyüklüyü (uzunluğu), istiqaməti və tətbiq nöqtəsi (vektorun başlanğıcı) olan obyekt başa düşülür.

Vektor hesabının başlanğıcı 1831-ci ildə alman riyaziyyatçısı, mexaniki, fiziki, astronomu və geodezisti İohann Karl Fridrix Qaussun (1777-1855) əsərlərində ortaya çıxdı. Vektorlarla əməliyyatlar üzərində işlər İrlandiyalı riyaziyyatçı, mexanik və nəzəri fizik Ser William Rowan Hamilton (1805-1865) tərəfindən quaternion hesablamasının bir hissəsi kimi nəşr edilmişdir. Alim "vektor" terminini təklif etdi və vektorlar üzərində bəzi əməliyyatları təsvir etdi. İngilis fiziki, riyaziyyatçısı və mexaniki Ceyms Klerk Maksvell (1831-1879) tərəfindən elektromaqnetizm üzərində aparılan işlər sayəsində vektor hesablaması daha da inkişaf etdirilmişdir. 1880-ci illərdə amerikalı fizik, fizikokimyaçı, riyaziyyatçı və mexanik Coziya Uillard Gibbsin (1839-1903) "Vektor analizinin elementləri" kitabı işıq üzü gördü. Müasir vektor analizi 1903-cü ildə ingilis özünü öyrədən alim, mühəndis, riyaziyyatçı və fizik Oliver Heaviside (1850-1925) tərəfindən təsvir edilmişdir.

TƏrif

Uzunluq və ya vektor modulu vektoru təyin edən istiqamətlənmiş seqmentin uzunluğudur. kimi göstərilir.

Vektorların əsas növləri

Sıfır vektor başlanğıc və son nöqtələri üst-üstə düşən vektordur. Sıfır vektorunun uzunluğu sıfırdır.

Bir düz xəttə paralel və ya bir düz xətt üzərində uzanan vektorlara deyilir kollinear(şək. 2).

birgə rejissorluq etmişdir onların istiqamətləri üst-üstə düşərsə.

Şəkil 2-də bunlar vektorlardır və. Vektorların birgə istiqamətliliyi aşağıdakı kimi işarələnir:.

İki kollinear vektor deyilir əks istiqamətə yönəldilib onların istiqamətləri əks olarsa.

Şəkil 3-də bunlar vektorlardır və. Təyinat:.

VEKTORLAR... TƏDBİRLƏRYUXARIDAVEKTORLAR. SKALAR,

VEKTOR, VEKTORLARIN QARIŞIQ MƏHSULU.

1. VEKTORLAR, VEKTORLAR ÜZRƏ HƏRƏKƏT.

Əsas təriflər.

Tərif 1. Seçilmiş vahidlər sistemində ədədi dəyəri ilə tam xarakterizə olunan kəmiyyət deyilir skalyar və ya skalyar .

(Bədən çəkisi, həcm, vaxt və s.)

Tərif 2.Ədədi dəyəri və istiqaməti ilə xarakterizə olunan kəmiyyət deyilir vektor və ya vektor .

(yerdəyişmə, güc, sürət və s.)

Təyinatlar:, və ya,.

Həndəsi vektor istiqamətli xəttdir.

Bir vektor üçün - bir nöqtə A- başlanğıc, nöqtə V- vektorun sonu.

Tərif 3.Modul vektor AB seqmentinin uzunluğudur.

Tərif 4. Modulu sıfıra bərabər olan vektor deyilir sıfır , tərəfindən göstərilir.

Tərif 5. Paralel xətlər üzərində və ya bir xətt üzərində yerləşən vektorlar deyilir kollinear ... İki kollinear vektor eyni istiqamətə malikdirsə, o zaman onlara deyilir birgə rejissorluq etmişdir .

Tərif 6.İki vektor nəzərə alınır bərabərdir , əgər onlar birgə rejissorluq etmişdir və mütləq dəyər baxımından bərabərdirlər.

Vektorlar üzərində hərəkətlər.

1) Vektorların əlavə edilməsi.

Def. 6.Məbləğ iki vektor və onların tətbiqinin ümumi nöqtəsindən başlayaraq bu vektorlar üzərində qurulmuş paraleloqramın diaqonalıdır. (paraleloqram qaydası).

Şəkil 1.

Def. 7.Üç vektorun cəminə,, bu vektorlar üzərində qurulmuş paralelepipedin diaqonalı deyilir (qutu qaydası).

Def. səkkiz.Əgər A, V, İLƏ İxtiyari nöqtələrdir, onda + = (üçbucaq qaydası).

şəkil 2

Əlavə xassələri.

1 O . + = + (transpozisiya qanunu).

2 O . + (+) = (+) + = (+) + (birləşmə qanunu).

3 O . + (– ) + .

2) Vektorların çıxılması.

Def. doqquz. Altında fərq vektorları və vektoru başa düşmək = - belə ki, + = .

Paraleloqramda bu başqadır diaqonal SD (Şəkil 1-ə baxın).

3) Bir vektorun ədədə vurulması.

Def. on. Məhsula görə skalar başına vektorlar k vektor adlanır

= k = k ,

uzun ka , və hansı istiqamət:

1.əgər vektorun istiqaməti ilə üst-üstə düşür k > 0;

2.Vektorun istiqamətinə əks, əgər k < 0;

3. əgər özbaşına k = 0.

Bir vektorun ədədə vurulmasının xassələri.

1 O . (k + l ) = k + l .

k ( + ) = k + k .

2 o . k (l ) = (kl ) .

3 o . 1  = , (–1)  = – , 0  = .

Vektor xassələri.

Def. on bir.İki vektor və adlanır kollinear üzərində yerləşirlərsə paralel xətlər ya da bir düz xətt.

Null vektoru istənilən vektorla kollineardır.

Teorem 1.İki sıfırdan fərqli vektor və kollinear,  mütənasib olduqda, yəni.

= k , k Skalerdir.

Def. 12.Üç vektor,, adlanır düzbucaqlı əgər onlar hansısa müstəviyə paraleldirlərsə və ya onun içində uzanırlarsa.

Teorem 2.Üç sıfırdan fərqli vektor,, düzbucaqlı,  onlardan biri digər ikisinin xətti kombinasiyası olduqda, yəni.

= k + l , k , l - skalyarlar.

Vektorun oxa proyeksiyası.

Teorem 3. Vektorun oxa proyeksiyası (istiqamətləndirilmiş düz xətt) l vektorun uzunluğunun vektorun istiqaməti ilə oxun istiqaməti arasındakı bucağın kosinusu ilə hasilinə bərabərdir, yəni. = a  c os  ,  = ( , l).

2. VEKTOR KOORDİNATLARI

Def. 13. Koordinat oxları üzərində vektor proyeksiyaları Oh, OU, Оz cağırılır vektor koordinatları. Təyinat:  a x , a y , a z .

Vektor uzunluğu:

Misal: Vektorun uzunluğunu hesablayın.

Həll:

Nöqtələr arasındakı məsafə və düsturla hesablanır: .

Misal: M (2,3, -1) və K (4,5,2) nöqtələri arasındakı məsafəni tapın.

Koordinat şəklində vektorlar üzərində hərəkətlər.

Verilmiş vektorlar =  a x , a y , a z və =  b x , b y , b z .

1. (  )= a x  b x , a y  b y , a z  b z .

2.  =   a x ,  a y ,  a z, harada  Skalerdir.

Vektorların nöqtə hasili.

Tərif:İki vektorun nöqtə hasili altında və

bu vektorların uzunluqlarının onların arasındakı bucağın kosinusu ilə hasilinə bərabər olan ədəd kimi başa düşülür, yəni. = , ve vektorları arasındakı bucaqdır.

Nöqtə məhsulunun xüsusiyyətləri:

1.  =

2. ( + ) =

3.

4.

5. , skalyarlar haradadır.

6.iki vektor perpendikulyar (ortoqonal) olarsa .

7. əgər və yalnız əgər .

Koordinat şəklində nöqtə məhsulu: , harada və .

Misal: vektorların nöqtə hasilini tapın

Həll:

Vektor tutan vektorlar.

Tərif: İki vektorun vektor məhsulu vektor kimi başa düşülür ki, bunun üçün:

Modul bu vektorlar üzərində qurulmuş paraleloqramın sahəsinə bərabərdir, yəni. , burada vektorlar arasındakı bucaq və

Bu vektor vurulan vektorlara perpendikulyardır, yəni.

Vektorlar kollinear deyilsə, onda vektorların düzgün üçlüyünü təşkil edirlər.

Vektor məhsulunun xüsusiyyətləri:

(1) Faktorların sırası dəyişdirildikdə, vektor məhsulu modulu saxlayaraq işarəsini əksinə dəyişir, yəni.

2 .Vektor kvadratı sıfır vektoruna bərabərdir, yəni.

3 Skayar amil vektor məhsulunun işarəsindən kənara köçürülə bilər, yəni.

4 İstənilən üç vektor üçün bərabərlik

5 İki vektorun kollinearlığı üçün zəruri və kafi şərt və:

Koordinat şəklində vektor məhsulu.

Əgər vektorların koordinatları və , onda onların çarpaz məhsulu düsturla tapılır:

.

Sonra vektor məhsulunun tərifindən belə çıxır ki, paraleloqramın sahəsi vektorlar üzərində qurulur və düsturla hesablanır:

Misal: Təpələri (1; -1; 2), (5; -6; 2), (1; 3; -1) olan üçbucağın sahəsini hesablayın.

Həll: .

Sonra ABC üçbucağının sahəsi aşağıdakı kimi hesablanacaq:

,

Vektorların qarışıq məhsulu.

Tərif: Vektorların qarışıq (vektor-skalyar) hasilatı düsturla müəyyən edilən ədəddir: .

Qarışıq iş xüsusiyyətləri:

1. Qarışıq məhsul onun amillərinin tsiklik dəyişməsi altında dəyişmir, yəni. .

2. İki bitişik faktorun dəyişdirilməsi zamanı qarışıq məhsul öz işarəsini əksinə dəyişir, yəni. ...

3 Üç vektorun mütənasibliyi üçün zəruri və kafi şərt : =0.

4 Üç vektorun qarışıq hasilatı bu vektorlar üzərində qurulmuş paralelepipedin həcminə bərabərdir, əgər bu vektorlar sağ üçlük əmələ gətirirsə, artı işarəsi ilə, sol üçlük əmələ gətirirsə, mənfi işarəsi ilə götürülür, yəni. .

Bilinsə koordinatları vektorlar , onda qarışıq iş düsturla tapılır:

Misal: Vektorların qarışıq hasilini hesablayın.

Həll:

3. Vektorlar sisteminin əsasları.

Tərif. Vektorlar sistemi dedikdə, eyni fəzaya aid olan bir neçə vektor başa düşülür R.

Şərh. Sistem sonlu sayda vektordan ibarətdirsə, onda onlar müxtəlif indekslərlə eyni hərflə işarələnirlər.

Misal.

Tərif. Formanın istənilən vektoru = vektorların xətti kombinasiyası adlanır. Rəqəmlər xətti birləşmənin əmsallarıdır.

Misal. .

Tərif... Əgər vektor vektorların xətti kombinasiyasıdırsa , onda vektorun vektorlarla xətti olaraq ifadə edildiyi deyilir .

Tərif. Vektor sistemi adlanır xətti müstəqil sistemin vektorlarından heç biri qalan vektorların xətti kombinasiyası kimi ola bilməzsə. Əks halda, sistem xətti asılı adlanır.

Misal... Vektor sistemi vektordan bəri xətti asılıdır .

Əsasın müəyyən edilməsi. Vektorlar sistemi aşağıdakı hallarda əsas təşkil edir:

1) xətti müstəqildir,

2) fəzanın istənilən vektoru onun vasitəsilə xətti olaraq ifadə edilir.

Misal 1. Kosmik əsas:.

2. Vektorlar sistemində vektorlar əsasdır: vektorlarla xətti olaraq ifadə edilir.

Şərh. Verilmiş vektor sisteminin əsasını tapmaq üçün sizə lazımdır:

1) vektorların koordinatlarını matrisə yazın,

2) matrisi üçbucaqlı formaya gətirmək üçün elementar çevrilmələrdən istifadə edərək,

3) matrisin sıfırdan fərqli sətirləri sistemin əsasını təşkil edəcək,

4) bazisdəki vektorların sayı matrisin dərəcəsinə bərabərdir.

üçün tapşırıqlar olacaq müstəqil qərar cavablarını görə bilərsiniz.

Vektor konsepsiyası

Vektorlar və onlar üzərində əməliyyatlar haqqında hər şeyi öyrənməzdən əvvəl sadə məsələnin həllinə kökləyin. Sahibkarlığınızın bir vektoru və yenilikçi qabiliyyətlərinizin vektoru var. Sahibkarlığın vektoru sizi Məqsəd 1-ə, innovativ qabiliyyətlərin vektoru isə Məqsəd 2-ə aparır. Oyunun qaydaları elədir ki, siz bu iki vektorun istiqamətlərində bir anda hərəkət edib iki məqsədə birdən nail ola bilməzsiniz. Vektorlar qarşılıqlı təsir göstərir və ya riyazi dillə desək, vektorlar üzərində bəzi əməliyyatlar yerinə yetirilir. Bu əməliyyatın nəticəsi sizi Məqsəd 3-ə aparan "Nəticə" vektorudur.

İndi mənə deyin: “Müəssisə” və “İnnovativ qabiliyyətlər” vektorları üzərində hansı əməliyyatın nəticəsi “Nəticə” vektorudur? Dərhal deyə bilmirsinizsə, ruhdan düşməyin. Bu dərsdə irəlilədikcə bu suala cavab verə biləcəksiniz.

Yuxarıda gördüyümüz kimi vektor mütləq hansısa nöqtədən gedir A bir nöqtəyə qədər düz xətt B... Nəticə etibarı ilə hər bir vektor təkcə ədədi qiymətə - uzunluğa deyil, həm də fiziki və həndəsi istiqamətə malikdir. Bu vektorun ilk və ən sadə tərifinə gətirib çıxarır. Deməli, vektor bir nöqtədən gedən istiqamətlənmiş seqmentdir A nöqtəsinə B... Aşağıdakı kimi təyin olunur:.

Və fərqli başlamaq üçün vektor əməliyyatları , vektorun daha bir tərifi ilə tanış olmalıyıq.

Vektor hansısa başlanğıc nöqtəsindən əldə etmək istədiyiniz nöqtənin bir növ təmsilidir. Məsələn, üçölçülü vektor adətən belə yazılır (x, y, z) . Çox sadə desək, bu rəqəmlər bir nöqtəyə çatmaq üçün üç fərqli istiqamətdə səyahət etməyin nə qədər vaxt lazım olduğunu göstərir.

vektor verilsin. Harada x = 3 (sağ əl sağa işarə edir) y = 1 (sol əl irəli göstərir) z = 5 (nöqtənin altında yuxarı qalxan bir pilləkən var). Bu məlumatlara görə, siz sağ əlinizin göstərdiyi istiqamətdə 3 metr, sonra sol əlinizin göstərdiyi istiqamətdə 1 metr, daha sonra sizi bir pilləkən gözləyir və 5 metr qalxaraq, nəhayət, bir nöqtə tapacaqsınız. özünüzü son nöqtədə tapın.

Bütün digər terminlər vektorlar üzərində müxtəlif əməliyyatlar, yəni praktiki məsələlərin həlli üçün zəruri olan yuxarıdakı izahatın təkmilləşdirmələridir. Tipik vektor problemləri üzərində dayanaraq, bu daha sərt tərifləri nəzərdən keçirək.

Fiziki nümunələr vektor kəmiyyətləri kosmosda hərəkət edən maddi nöqtənin yerdəyişməsi, bu nöqtənin sürəti və sürətlənməsi, həmçinin ona təsir edən qüvvə ola bilər.

Həndəsi vektorşəklində ikiölçülü və üçölçülü fəzada təqdim olunur istiqamətli seqment... Bu, başlanğıc və son arasında fərq qoyan seqmentdir.

Əgər A vektorun başlanğıcıdır və B- onun sonu, sonra vektor simvol və ya bir kiçik hərflə işarələnir. Şəkildə vektorun sonu ox ilə göstərilmişdir (şək. 1)

Uzunluq(və ya modul) həndəsi vektorun onu yaradan seqmentin uzunluğudur

İki vektor deyilir bərabərdir paralel köçürmə yolu ilə düzülə bilsələr (istiqamətlər üst-üstə düşürsə), yəni. paraleldirlərsə, eyni istiqamətə yönəldin və bərabər uzunluqlara malikdirlər.

Fizikada buna tez-tez baxılır bağlanmış vektorlar tətbiq nöqtəsi, uzunluğu və istiqaməti ilə verilir. Vektorun tətbiqi nöqtəsi əhəmiyyət kəsb etmirsə, o zaman uzunluğu və istiqamətini kosmosda istənilən nöqtəyə saxlamaqla ötürülə bilər. Bu halda vektor çağırılır pulsuz... Biz yalnız nəzərə almağa razılaşacağıq Pulsuz vektorlar.

Həndəsi vektorlar üzərində xətti əməliyyatlar

Bir vektorun ədədə vurulması

Vektor məhsulu nömrə ilə vektordan dəfələrlə genişlənmə (at) və ya sıxılma (at) yolu ilə alınan vektor deyilir və vektorun istiqaməti if saxlanılır və əgər əks istiqamətdə dəyişir. (Şəkil 2)

Tərifdən belə çıxır ki, və = vektorları həmişə bir və ya paralel xətlər üzərində yerləşir. Belə vektorlar deyilir kollinear... (Həmçinin deyə bilərsiniz ki, bu vektorlar paraleldir, lakin vektor cəbrində "kollinear" demək adətdir.) Əksi də doğrudur: vektorlar və kollineardırlarsa, onda onlar əlaqə ilə əlaqələndirilir.

Buna görə də (1) bərabərliyi iki vektor üçün kollinearlıq şərtini ifadə edir.

Vektorların toplanması və çıxılması

Vektorları əlavə edərkən bunu bilmək lazımdır məbləğ vektordur və vektor adlanır, başlanğıcı vektorun əvvəli ilə, sonu isə vektorun sonu ilə üst-üstə düşür, bu şərtlə ki, vektorun başlanğıcı vektorun sonuna əlavə olunsun. (Şəkil 3)

Bu tərif istənilən sonlu sayda vektor üzərində paylana bilər. Yer verilsin n Pulsuz vektorlar. Bir neçə vektor əlavə edilərkən onların cəmi kimi bağlanma vektoru götürülür, başlanğıcı birinci vektorun əvvəlinə, sonu isə sonuncu vektorun sonu ilə üst-üstə düşür. Yəni vektorun əvvəlini vektorun sonuna, vektorun başlanğıcını vektorun sonuna əlavə etsəniz və s. və nəhayət, vektorun sonuna - vektorun başlanğıcına qədər, sonra bu vektorların cəmi bağlanan vektordur. başlanğıcı birinci vektorun başlanğıcı ilə, sonu isə sonuncu vektorun sonu ilə üst-üstə düşür. (Şəkil 4)

Terminlər vektorun komponentləri adlanır və tərtib edilmiş qayda belədir çoxbucaqlı qayda... Bu çoxbucaqlı düz olmaya bilər.

Bir vektoru -1-ə vurduqda əks vektoru alırsınız. Vektorlar və eyni uzunluğa və əks istiqamətlərə malikdirlər. Onların məbləği verir sıfır vektor uzunluğu sıfır olan. Sıfır vektorunun istiqaməti qeyri-müəyyəndir.

Vektor cəbrində çıxma əməliyyatını ayrıca nəzərdən keçirməyə ehtiyac yoxdur: vektordan vektoru çıxarmaq vektora əks vektor əlavə etmək deməkdir, yəni.

Misal 1.İfadəni sadələşdirin:

.

,

yəni vektorlar çoxhədlilərlə eyni şəkildə əlavə edilə və ədədlərə vurula bilər (xüsusən də ifadələrin sadələşdirilməsi üzrə tapşırıqlar). Adətən vektorların məhsullarını hesablamazdan əvvəl xətti oxşar ifadələrin vektorlarla sadələşdirilməsi zərurəti yaranır.

Misal 2. vektorları ABCD paraleloqramının diaqonalları kimi xidmət edir (şək. 4a). Bu paraleloqramın tərəfləri olan və hər iki vektoru ilə ifadə edin.

Həll. Paraleloqram diaqonallarının kəsişmə nöqtəsi hər diaqonalı yarıya bölür. Problemin ifadəsində tələb olunan vektorların uzunluqlarını ya arzu olunanlarla üçbucaq təşkil edən vektorların cəminin yarısı, ya da fərqlərin yarısı (diaqonal kimi xidmət edən vektorun istiqamətindən asılı olaraq) və ya kimi tapırıq. ikinci halda, mənfi işarə ilə alınan məbləğin yarısı. Nəticə problem bəyanatında tələb olunan vektorlardır:

İndi bu dərsin əvvəlində Sahibkarlıq və İnnovativ Bacarıq vektorları ilə bağlı suala düzgün cavab verdiyinizi düşünmək üçün hər cür əsas var. Düzgün cavab: bu vektorlar üzərində toplama əməliyyatı aparılır.

Vektor problemlərini özünüz həll edin və sonra həll yollarına baxın

Vektorların cəminin uzunluğunu necə tapmaq olar?

Bu tapşırıq vektor əməliyyatlarında xüsusi yer tutur, çünki o, triqonometrik xassələrin istifadəsini nəzərdə tutur. Deyək ki, aşağıdakı kimi bir vəzifə ilə qarşılaşdınız:

Vektorların uzunluqlarını nəzərə alaraq və bu vektorların cəminin uzunluğu. Bu vektorların fərqinin uzunluğunu tapın.

Bu və digərləri üçün həllər oxşar vəzifələr və onları necə həll etməyin izahı - dərsdə " Vektor əlavəsi: vektor cəmi uzunluğu və kosinus teoremi ".

Və bu kimi problemlərin həllini yoxlaya bilərsiniz Onlayn kalkulyator "Üçbucağın naməlum tərəfi (vektor əlavəsi və kosinus teoremi)" .

Vektorların məhsulları haradadır?

Bir vektorun vektorun hasilləri xətti əməliyyatlar deyil və ayrıca nəzərdən keçirilir. Və "Vektor nöqtə hasili" və "Vektor və vektorların qarışıq hasilatı" dərslərimiz var.

Vektorun oxa proyeksiyası

Vektorun oxa proyeksiyası proyeksiya edilən vektorun uzunluğunun vektorla ox arasındakı bucağın kosinusu ilə hasilinə bərabərdir:

Bildiyiniz kimi, nöqtənin proyeksiyası A düz xətt üzərində (müstəvidə) bu nöqtədən düz xəttə (müstəvi) salınan perpendikulyarın əsasıdır.

İxtiyari vektor olsun (şək. 5) və onun başlanğıcının (nöqtələrinin) proyeksiyaları olsun. A) və son (nöqtə B) hər ox l... (Nöqtənin proyeksiyasını qurmaq üçün A) nöqtədən keçən düz xətt üzərində A düz xəttə perpendikulyar olan müstəvi. Xəttin və təyyarənin kəsişməsi tələb olunan proyeksiyanı təyin edəcəkdir.

Vektor komponenti l oxunda bu oxda yatan vektor adlanır, onun başlanğıcı başlanğıcın proyeksiyası ilə, sonu isə vektorun sonunun proyeksiyası ilə üst-üstə düşür.

Vektorun oxa proyeksiyası l nömrəyə zəng etdi

,

komponentin istiqaməti oxun istiqaməti ilə üst-üstə düşürsə, bu oxda komponent vektorunun uzunluğuna bərabərdir, əlavə işarəsi ilə qəbul edilir. l, və bu istiqamətlər əks olarsa mənfi işarəsi ilə.

Oxa vektor proyeksiyalarının əsas xassələri:

1. Bərabər vektorların eyni oxa proyeksiyaları bir-birinə bərabərdir.

2. Vektoru ədədə vurarkən onun proyeksiyası eyni ədədə vurulur.

3. İstənilən ox üzrə vektorların cəminin proyeksiyası vektorların cəmlərinin eyni ox üzrə proyeksiyalarının cəminə bərabərdir.

4. Vektorun oxa proyeksiyası proyeksiya edilən vektorun uzunluğunun vektorla ox arasındakı bucağın kosinusuna hasilinə bərabərdir:

.

Həll. Vektorları bir oxa layihələndirin l yuxarıdakı nəzəri fonda müəyyən edildiyi kimi. Şəkil 5a-dan aydın olur ki, vektorların cəminin proyeksiyası vektorların proyeksiyalarının cəminə bərabərdir. Bu proqnozları hesablayırıq:

Vektorların cəminin son proyeksiyasını tapın:

Kosmosda düzbucaqlı Dekart koordinat sistemi ilə vektorun əlaqəsi

ilə tanışlıq kosmosda düzbucaqlı Dekart koordinat sistemi müvafiq dərsdə baş verdi, onu yeni pəncərədə açmaq arzu edilir.

Sifarişli koordinat sistemində 0xyz ox öküzçağırdı absis, ox 0y – y oxu, və ox 0z – ox tətbiq olunur.

İxtiyari bir nöqtə ilə M vektoru əlaqələndirdiyimiz fəza

çağırdı radius vektoru xal M və onu koordinat oxlarının hər birinə proyeksiya edin. Müvafiq proqnozların dəyərlərini qeyd edək:

Rəqəmlər x, y, z cağırılır M nöqtəsinin koordinatları, müvafiq olaraq absis, ordinasiya etmək və müraciət etmək, və ədədlərin düzülmüş nöqtəsi kimi yazılır: M (x; y; z)(şək. 6).

İstiqaməti oxun istiqaməti ilə üst-üstə düşən vahid uzunluqlu vektor adlanır vahid vektor(və ya ortom) ox. ilə işarə edək

Müvafiq olaraq koordinat oxlarının vahid vektorları öküz, ay, Oz

teorem.İstənilən vektor koordinat oxlarının vahid vektorları boyunca genişləndirilə bilər:

(2)

Bərabərlik (2) vektorun koordinat oxları boyunca genişlənməsi adlanır. Bu genişlənmənin əmsalları vektorun koordinat oxlarına proyeksiyalarıdır. Beləliklə, vektorun koordinat oxları boyunca genişlənmə əmsalları (2) vektorun koordinatlarıdır.

Kosmosda müəyyən bir koordinat sistemi seçildikdən sonra vektor və onun koordinatlarının üçlüyü bir-birini unikal şəkildə təyin edir, beləliklə vektor formada yazıla bilər.

(2) və (3) formasında vektorun təsvirləri eynidir.

Koordinatlarda vektorlar üçün kollinearlıq şərti

Artıq qeyd etdiyimiz kimi, vektorlar əlaqə ilə əlaqəli olduqda kollinear adlanır

Qoy vektorlar ... Əgər vektorların koordinatları əlaqə ilə bağlıdırsa, bu vektorlar kollinear olur

,

yəni vektorların koordinatları mütənasibdir.

Misal 6. Verilmiş vektorlar ... Bu vektorlar kollineardırmı?

Həll. Bu vektorların koordinatlarının nisbətini öyrənək:

.

Vektorların koordinatları mütənasibdir, buna görə vektorlar kollinear və ya eyni olan paraleldir.

Vektor uzunluğu və istiqamət kosinusları

Koordinat oxlarının qarşılıqlı perpendikulyarlığına görə vektorun uzunluğu

vektorlar üzərində qurulmuş düzbucaqlı paralelepipedin diaqonalının uzunluğuna bərabərdir

və bərabərliklə ifadə olunur

(4)

Vektor iki nöqtəni (başlanğıc və son) göstərməklə tamamilə müəyyən edilir, buna görə vektorun koordinatları bu nöqtələrin koordinatları ilə ifadə edilə bilər.

Verilmiş koordinat sistemində vektorun başlanğıcı nöqtədə olsun

və son nöqtədədir

Bərabərlikdən

Bunu izləyir

və ya koordinat şəklində

Beləliklə, vektorun koordinatları vektorun sonu və əvvəlinin eyni adlı koordinatlarının fərqinə bərabərdir ... Formula (4) bu halda formanı alır

Vektorun istiqaməti ilə müəyyən edilir istiqamət kosinusları ... Bunlar vektorun oxlarla əmələ gətirdiyi bucaqların kosinuslarıdır öküz, ay və Oz... Bu açıları müvafiq olaraq işarə edək α , β və γ ... Sonra bu bucaqların kosinuslarını düsturlarla tapmaq olar

Bir vektorun istiqamətli kosinusları da bu vektorun vahid vektorunun koordinatlarıdır və deməli, vektor vektorudur.

.

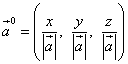
Vektor vahidinin uzunluğunun bir vahidə bərabər olduğunu nəzərə alsaq, yəni

,

istiqamət kosinusları üçün aşağıdakı bərabərliyi əldə edirik:

Misal 7. Bir vektorun uzunluğunu tapın x = (3; 0; 4).

Həll. Vektor uzunluğudur

Misal 8. Xallar verilir:

Bu nöqtələr üzərində qurulmuş üçbucağın ikitərəfli olub olmadığını öyrənin.

Həll. (6) vektorunun uzunluğu üçün düsturdan istifadə edərək, tərəflərin uzunluqlarını tapırıq və onların arasında iki bərabər olanın olub olmadığını müəyyən edirik:

İki bərabər tərəf tapıldı, ona görə də üçüncü tərəfin uzunluğunu axtarmağa ehtiyac yoxdur və verilən üçbucaq ikitərəflidir.

Misal 9.Əgər vektorun uzunluğunu və onun istiqamət kosinuslarını tapın .

Həll. Vektor koordinatları verilir:

.

Vektor uzunluğudur kvadrat kök vektorun koordinatlarının kvadratlarının cəmindən:

.

İstiqamət kosinuslarını tapın:

Vektor problemini özünüz həll edin və sonra həllinə baxın

Koordinat şəklində göstərilən vektorlar üzərində əməliyyatlar

İki vektor verilsin və onların proyeksiyaları ilə verilsin:

Bu vektorlar üzərində hərəkətləri göstərək.

Yaradılma Tarixi: 2009-04-11 15:25:51
Son redaktə: 2012-02-08 09:19:45

Uzun müddət bu yazını yazmaq istəmirdim - materialı necə təqdim edəcəyimi düşünürdüm. Siz həmçinin şəkillər çəkmək lazımdır. Amma görürsünüz ki, ulduzlar bu gün uğurla formalaşıb və vektorlar haqqında məqalə olacaq. Baxmayaraq ki, bu sadəcə kobud bir layihədir. Gələcəkdə bu məqaləni bir neçə ayrı məqaləyə ayıracağam - kifayət qədər material var. Həm də məqalə tədricən təkmilləşəcək: ona dəyişikliklər edəcəm. bir oturuşda bütün cəhətləri açmaq mümkün olmayacaq.

Skalar qiymətlərdən istifadə edərək təsvir etmək çətin olan kəmiyyətləri təsvir etmək üçün vektorlar XIX əsrdə riyaziyyata daxil edilmişdir.

Vektorlardan kompüter oyunlarının inkişafında geniş istifadə olunur. Onlar yalnız ənənəvi olaraq deyil - güc və ya sürət kimi kəmiyyətləri təsvir etmək üçün, həm də vektorlarla heç bir əlaqəsi olmayan sahələrdə istifadə olunur: rəngin saxlanması, kölgələrin yaradılması.

Skalar və vektorlar

Əvvəlcə sizə skalyarın nə olduğunu və vektordan nə ilə fərqləndiyini xatırlatdım.

Skalyar dəyərlər müəyyən bir miqdar saxlayır: kütlə, həcm. Yəni, yalnız bir rəqəmlə (məsələn, bir şeyin miqdarı) xarakterizə olunan bir varlıqdır.

Skayardan fərqli olaraq vektor iki qiymətdən istifadə etməklə təsvir olunur: böyüklük və istiqamət.

Vektorlar və koordinatlar arasında mühüm fərq: vektorlar müəyyən bir yerə bağlı deyil! Bir daha qeyd edirəm ki, vektorda əsas şey uzunluq və istiqamətdir.

Vektor latın əlifbasının qalın hərfi ilə işarələnir. Misal üçün: a, b, v.

Birinci şəkildə vektorun təyyarədə necə təyin olunduğunu görə bilərsiniz.

Kosmosda vektorlar

Kosmosda vektorları koordinatlardan istifadə etməklə ifadə etmək olar. Ancaq əvvəlcə bir konsepsiya təqdim etməlisiniz:

Nöqtə radius vektoru

Fəzada hansısa M (2,1) nöqtəsini götürün. Nöqtənin radius vektoru başlanğıcdan başlayan və nöqtədə bitən vektordur.

Burada vektordan başqa bir şeyimiz yoxdur OM... Vektor başlanğıc koordinatları (0,0), son koordinatları (2,1). Bu vektoru kimi işarə edirik a.

Bu halda vektor aşağıdakı kimi yazıla bilər a = <2, 1>... Bu vektorun koordinat formasıdır a.

Vektorun koordinatlarına onun oxlara nisbətən komponentləri deyilir. Məsələn, 2 vektor komponentidir a x oxu haqqında.

Nöqtə koordinatlarının nə olduğuna bir daha nəzər salaq. Nöqtənin koordinatı (məsələn, x) bir nöqtənin oxa proyeksiyasıdır, yəni. perpendikulyarın əsası bir nöqtədən bir oxa düşdü. Bizim nümunəmizdə 2.

Ancaq birinci şəkilə qayıdaq. Burada iki A və B nöqtəmiz var. Nöqtələrin koordinatları (1,1) və (3,3) olsun. Vektor v bu halda aşağıdakı kimi işarələmək olar v = <3-1, 3-1>... Üçölçülü fəzada iki nöqtədə yerləşən vektor belə görünəcək:

v =

Düşünürəm ki, burada heç bir çətinlik yoxdur.

Bir vektorun skalara vurulması

Bir vektor skalyar qiymətlərlə vurula bilər:

k v = =

Bu, vektorun hər bir komponenti ilə skalyar dəyəri çoxaldır.

Əgər k> 1 olarsa, vektor artacaq, k birdən kiçik, lakin sıfırdan böyükdürsə, vektorun uzunluğu azalacaq. Əgər k sıfırdan kiçikdirsə, vektor istiqamətini dəyişəcək.

Vahid vektorları

Vahid vektorlar uzunluğu birə bərabər olan vektorlardır. Koordinatları olan vektora diqqət yetirin<1,1,1>birinə bərabər olmayacaq! Vektorun uzunluğunu tapmaq mətndə aşağıda təsvir edilmişdir.

Sözdə vahid vektorlar var - bunlar koordinat oxları ilə istiqamətdə üst-üstə düşən vahid vektorlardır. i- x oxunun vahid vektoru, j- y oxunun vahid vektoru, k z oxunun vahid vektorudur.

Harada i = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

İndi vektorun skalyarla vurulmasının nə olduğunu və vahid vektorların nə olduğunu bilirik. İndi yaza bilərik v vektor şəklində.

v= v x i+ v y j+ v z k, burada v x, v y, v z vektorun uyğun komponentləridir

Vektor əlavəsi

Əvvəlki düsturu tam başa düşmək üçün vektor əlavəsinin necə işlədiyini başa düşməlisiniz.

Burada hər şey sadədir. İki v1 = vektorunu götürün və v 2 =

v 1 + v 2 =

Biz sadəcə olaraq iki vektorun müvafiq komponentlərini əlavə edirik.

Fərq eyni şəkildə hesablanır.

Bu, riyazi formaya aiddir. Tamlıq üçün vektorların əlavə və çıxmasının qrafik olaraq necə görünəcəyini düşünməyə dəyər.

İki vektor əlavə etmək üçün a+b... Vektorun başlanğıcına uyğun gəlməlisiniz b və vektorun sonu a... Sonra vektorun başlanğıcı arasında a və vektorun sonu b yeni vektor çəkin. Aydınlıq üçün ikinci rəqəmə ("a" hərfi) baxın.

Vektorları çıxmaq üçün iki vektorun başlanğıcını birləşdirib ikinci vektorun sonundan birincinin sonuna qədər yeni vektor çəkmək lazımdır. İkinci şəkil ("b" hərfi) necə göründüyünü göstərir.

Vektor uzunluğu və istiqaməti

Əvvəlcə uzunluğa baxaq.

Uzunluq istiqamət istisna olmaqla vektorun ədədi dəyəridir.

Uzunluq düsturla müəyyən edilir (üç ölçülü vektor üçün):

vektor komponentlərinin kvadratlarının cəminin kvadrat kökü.

Tanış bir düstur, elə deyilmi? Ümumiyyətlə, bu, bir seqmentin uzunluğu üçün düsturdur

Vektorun istiqaməti vektor və koordinat oxları arasında əmələ gələn bucaqların istiqamət kosinusları ilə müəyyən edilir. İstiqamət kosinuslarını tapmaq üçün müvafiq komponentlər və uzunluqdan istifadə olunur (şəkil daha sonra olacaq).

Proqramlarda vektorların təmsil olunması

Proqramlarda vektorları müxtəlif üsullarla təmsil edə bilərsiniz. Həm effektiv olmayan adi dəyişənlərin, həm də massivlərin, siniflərin və strukturların köməyi ilə.

Float vektor3 = (1,2,3); // vektor strukturunun saxlanması üçün massiv vektor3 // vektorların saxlanması üçün struktur (float x, y, z;);

Vektorların saxlanması üçün ən böyük imkanlar siniflər tərəfindən təmin edilir. Dərslərdə biz təkcə vektorun özünü (dəyişənləri) deyil, həm də vektor əməliyyatlarını (funksiyalarını) təsvir edə bilərik.

Vektorların nöqtə hasili

Vektor vurulmasının iki növü var: vektor və skalyar.

Nöqtə məhsulunun fərqli bir xüsusiyyəti, nəticənin həmişə skalyar bir dəyər olacağıdır, yəni. nömrə.

Burada aşağıdakı məqama diqqət yetirməyə dəyər. Bu əməliyyatın nəticəsi sıfırdırsa, onda iki vektor perpendikulyardır - aralarındakı bucaq 90 dərəcədir. Nəticə sıfırdan böyükdürsə, bucaq 90 dərəcədən azdır. Nəticə sıfırdan azdırsa, bucaq 90 dərəcədən böyükdür.

Bu əməliyyat aşağıdakı düsturla təmsil olunur:

a · b= a x * b x + a y * b y + a z * b z

Nöqtə hasili iki vektorun müvafiq komponentlərinin hasillərinin cəmidir. Bunlar. İki vektorun x "s-ni götürün, onları çoxaldın, sonra y" s-nin hasili ilə əlavə edin və s.

Vektorların vektor məhsulu

İki vektorun çarpaz hasilinin nəticəsi bu vektorlara perpendikulyar vektor olacaq.

a x b =

Bu düsturu hələ ətraflı müzakirə etməyəcəyik. Üstəlik, onu yadda saxlamaq olduqca çətindir. Determinantlarla tanış olduqdan sonra bu məqama qayıdacağıq.

Yaxşı, ümumi inkişaf üçün nəticədə vektorun uzunluğunun vektorlar üzərində qurulmuş paraleloqramın sahəsinə bərabər olduğunu bilmək faydalıdır. a və b.

Vektor normallaşması

Normallaşdırılmış vektor uzunluğu bir olan vektordur.

Normallaşdırılmış vektoru tapmaq üçün formula aşağıdakı kimidir - vektorun bütün komponentləri onun uzunluğuna bölünməlidir:

v n = v/ | v | =

Son söz

Yəqin ki, gördüyünüz kimi vektorları başa düşmək çətin deyil. Biz vektorlar üzərində bir sıra əməliyyatları əhatə etdik.

"Riyaziyyat" bölməsinin növbəti məqalələrində biz matrisləri, determinantları, sistemləri müzakirə edəcəyik xətti tənliklər... Bütün bunlar nəzəriyyədir.

Bundan sonra matris çevrilmələrinə baxacağıq. Məhz o zaman siz kompüter oyunlarının yaradılmasında riyaziyyatın nə qədər vacib olduğunu başa düşəcəksiniz. Bu mövzu sadəcə olaraq bütün əvvəlki mövzular üçün praktikaya çevriləcək.